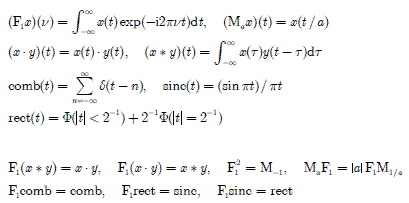| progC.pdf progC-s.pdf progC-e.pdf 記事一覧 |
 debug_hacks_09.pdf のスタックダンプの説明 |
progC-e.pdf に参考資料 と [#4: 関数] の後半を追加しました．
参考資料（[n]は本文でも引用, *.pptはブロック解除が面倒なので未調査）：
[1] HACK#9 デバッグに必要なスタックの基礎知識（685KB）
http://www.oreilly.co.jp/editors/debug_hacks_09.pdf
補足：(1) Ｃでも「if(i > k){int i1 =i; i = k; k = i1;}」のようにできることは K&R2，p.286（ブロックの先頭でなければならない）．
(2) gdb 実行中の画面
| progC.pdf progC-s.pdf progC-e.pdf 記事一覧 |
 仮引数の宣言 |
progC-e.pdf に[#4: 関数] の前半を追加しました．
参考資料（[n]は本文でも引用, *.pptはブロック解除が面倒なので未調査）：
[1] GNUアセンブラ - Wikipedia
http://ja.wikipedia.org/wiki/GNU%E3%82%A2%E3%82%BB%E3%83%B3%E3%83%96%E3%83%A9
[2] Using as
http://sourceware.org/binutils/docs-2.18/as/
[3] GCCコマンド・オプション
http://www.asahi-net.or.jp/~wg5k-ickw/html/online/gcc-2.95.2/gcc_2.html
出力の種類を制御するオプション・・・
-S 狭義のコンパイル処理段階の後に停止し、アセンブル処理を実行しません。出力形態は、指定された入力ファイルのうちアセンブラ・コードで記述されていないものに対するアセンブラ・コードのファイルとなります。
[4] コールスタック - Wikipedia
http://ja.wikipedia.org/wiki/%E3%82%B3%E3%83%BC%E3%83%AB%E3%82%B9%E3%82%BF%E3%83%83%E3%82%AF
-----
[5] 「アセンブリ言語の教科書」の原稿 - ruffnex
http://ruffnex.oc.to/kenji/text/asmbook/
[6] IA32 (x86) の命令セット
http://www.csg.ci.i.u-tokyo.ac.jp/~chiba/lecture/os/lang106.html
補足：(1) 関数の定義，呼び出しに関する説明は progC.pdf と重複するので省略しました．主として仮引数での宣言とこれまでの宣言の違いについて述べています．
(2) Prog4-1.s の実行結果
|
差し替え： 2013-11-20 |
 アナログモデルの公式 |
武部先生のゼミで再度 DFT でのゼロ詰めが話題になったので，Web で検索してみました．孤立波形の場合は本当のゼロなので，ゼロ詰めすれば当然周波数分解能は向上します．問題は，窓で切り出した波形を FFT を適用するために行った場合です．ゼロ詰めする前と後のスペクトルの関係を，アナログモデルで考えて見ましょう．
周期１で標本化された信号 x(t)comb(t) を長さ N の方形窓で切り取った信号を
y(t) = x(t)comb(t)rect((t - 2-1(N-1)) / N)
とします．y(t) のフーリエ変換は
(F1y)(ν) = (F1x)(ν) * comb(ν) * α sinc(Nν)
であり（αは定数），(F1y)(ν) = (F1y)(ν-1) なので
(F1y)(ν) = Y(ν) * comb(ν) ( Y(ν) = rect(ν)Y(ν) )
と表現できます（Y(ν) は (F1y)(ν) を周期１で折り返した関数）．Y(ν) を標本化した Y(ν)comb(Mν) を求めるということは y(t) * comb(t / M) のスペクトルを求めることに相当します（定数倍は無視）．
x(t) = Σk ck exp(i2πkt)
のスペクトルは exp(i2πkt) のスペクトルの加重加算なので，簡単のため x(t) = exp(i2πkt) とし，N が十分に大きいとして
Y(ν) ＝ (δ(ν - k) * comb(ν) * α sinc(Nν))rect(ν)
≒ α((sinc(N(ν - k)rect(ν - k)) * comb(ν))rect(ν)
と近似した場合について考えます．sinc(N(ν - k))comb(Nν) = δ(ν - k) なので M = N であれば窓の影響はありませんが，M ＞ N のときは Y(ν)comb(Mν) に ν = k の近傍に高調波が表れます．連続関数としての Y(ν) でなく，N 点 DFT の標本値がほしいときは，M ＞ 4 N 程度にして Y(ν) を折れ線近似したグラフを作り，１次補間で所望の周波数での値を近似できます--- M が大きいと Y(ν) は緩やかに変化します．
※ Y(ν) の近似式は α sinc(Nν)rect(ν) を巡回シフトしたもので α sinc(Nνk)rect(ν) (νk は (ν - k/N)，(ν - k/N + 1) のいずれか) と表現できます．
補足：(0) 周期に等しくない窓をかけると基本周波数近傍のスペクトルは原信号のスペクトルとは別物になっています．このことは窓より低い周波数の正弦波が基本波成分と多数の高調波成分に分解されてしまうことからも明らかです --- 非周期信号には通常（方形でない）窓をかけます．
(1) x(t) = exp(i2πkt) の例から，ゼロ詰めしたときのスペクトルをゼロ詰めしないときのスペクトルに変換する行列の sparsity を予想できます．
(2) sinc(Nν) との畳み込みによって輝線スペクトルが拡がる幅 Δν は ν に依存しないので周波数特性を log ν で考えるような分野では中高域の部分に窓の影響はあまりありません．
(3) 振幅変調された信号の場合，被変調波の帯域が 1/2 以下であればそのまま周期１で標本化して得られたスペクトルを搬送周波数に応じて巡回シフトすれば被変調波のスペクトルになります．
(4) rect(t) の定義を 旧sys-deleted.pdf から変えました．この結果，ほとんどいたるところでなく，厳密に (F1sinc)(ν) = rect(ν) が成立しますが，rect(t / N)comb(t) は N + 1 個の非 0 の標本値を持つことになり，周期が N でない関数の標本値を切り取るには上記のようなシフトが必要になります --- 煩わしいのですが，離散コサイン変換も視野に入れて，こちらに変更．
[1] FFT Zero Padding | BitWeenie
http://www.bitweenie.com/listings/fft-zero-padding/
If you apply a windowing function to your waveform, the windowing function needs to be
applied before zero padding the data.
[2] Zero Padding Does Not Buy Spectral Resolution - National ...
http://www.ni.com/white-paper/4880/en/
3. Padded Records Not Always a Good Fit
[3] 振幅推定とゼロ パディング - MATLAB & Simulink - MathWorks 日本
http://www.mathworks.co.jp/jp/help/signal/ug/amplitude-estimation-and-zero-padding.html
DFT を求める前にデータにゼロ パディングを行えば、振幅推定を改善する上で役立つことがよくあります。
[4] Padding with Zeros
http://www.cs.hmc.edu/~kperdue/zeroPadding.html
However, we must make sure that we are still getting a reasonable approximation of ・・・
[5] Increasing FFT resolution using zero padding using ...
http://forums.ni.com/t5/High-Speed-Digitizers/Increasing-FFT-resolution-using-zero-padding-using/td-p/2246228
[6] EE 4078: Zero-Padding the FFT - ECE User Home Pages
http://users.ece.gatech.edu/~mcclella/courses/ee4078/FFT-interpol.pdf
The zero padding must bee done "in the middle."
[7] FFTにおけるゼロ追加、補間や分解能について | 数学のQ&A【OKWave】
http://okwave.jp/qa/q3825994.html
http://soudan1.biglobe.ne.jp/qa3825994.html
[8] フーリエ変換について。 - Yahoo!知恵袋
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1331890093
[9] フーリエ変換のデータの補間について - 数学 - 教えて！goo
http://oshiete.goo.ne.jp/qa/5012398.html
[10] fft - Why should I zero-pad a signal before taking the Fourier ...
http://dsp.stackexchange.com/questions/741/why-should-i-zero-pad-a-signal-before-taking-the-fourier-transform
But, essentially, zero padding before a DFT/FFT is a computationally efficient method of ・・・
[11] Converting between zero padded and non zero padded FFT ...
http://www.mathworks.com/matlabcentral/answers/67326
| progC.pdf progC-s.pdf progC-e.pdf 記事一覧 |
 無限ループになる文字列のコピー |
progC-e.pdf に 「#3:配列とポインタ」 に関する部分を追加しました．
参考資料（[n]は本文でも引用, *.pptは未調査）：
[1] signalについて（前篇） （1/4）：CodeZine
http://codezine.jp/article/detail/1450?p=1
[2] MinGW 向けにコンパイルしたプログラムで Ctrl-C が効かなくて泣いて ...
http://d.hatena.ne.jp/kikairoya/20121017/1350449105
[3] C言語のプログラム実行中に、コンソールからCtrl-Cが押されたときには
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1218805427
[4] ポインタに関する資料はこちらを見てください．
http://blog.goo.ne.jp/bonsai-juku/e/f63cc617560826481a66885012fc71e6
補足：(1) ya-c.pdf で省略した素直でないポインタの使い方の例も示しました．ポインタ配列と多次元ポインタについては後半で演習します．関数の仮引数でのポインタ，関数へのポインタについては #4 で扱います．
(2) 参考資料はたぶん必要ないと思いますが，一応掲げておきます．
(3) 実行画面の例
