ディジタルフィルタ (4)

sys.pdf sys-s.pdf sys.txt 記事一覧

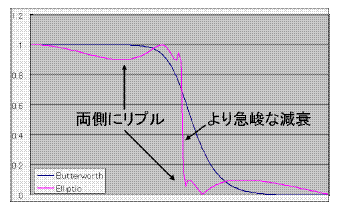[3-33] 楕円フィルタの周波数特性

#36: 周波数特性

正弦波（cos ωt, sin ωt, e^±iωt = cos ωt ± i sin ωt）は線形時不変な回路の固有関数です．すなわち，信号 x(t) を入力したときの出力が (Tx)(t) である回路 T に対して (Tx)(t) = λx(t) （λ：定数）となる x(t) は正弦波に限られます．x(t) = e^iωt のときのλはωに依存し，これをωの関数と考えて H(iω) と表し，周波数伝達関数といいます．H(iω) = A e^iφ（A ≧ 0，φは実数）とおくと，x(t) = sin ωt のときy(t) = A sin(ωt + φ) になります．離散時間の信号 y(n) についても同様です．

ω≦ω_c である正弦波をそのまま通し，ω＞ω_cである正弦波を遮断するフィルタを遮断角周波数 ω_c の理想低域通過フィルタといいます．実際にこれを作ることは不可能ですが近似的に実現する方法がいろいろ提案されています．

[3-30] フィルタ回路 - Wikipedia
  http://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A3%E3%83%AB%E3%82%BF%E5%9B%9E%E8%B7%AF
[3-31] ディジタルフィルタとｚ変換 ＜ [3-2] の「基礎編」chap10
  http://laputa.cs.shinshu-u.ac.jp/~yizawa/InfSys1/basic/chap10/index.htm
  後半に周波数特性
[3-32] 理想低域通過フィルタ
  http://www.mm.media.kyoto-u.ac.jp/education/dip/appendix/Fourier/node13.html
---------------------
[3-33] ディジタルフィルタ（目次）
  http://ufcpp.net/study/digital_filter/index.html
  バターワース，チェビシェフ，逆チェビシェフ，楕円
[3-34] ローパスフィルタの設計(チェビシェフフィルタ)
  http://robotics.me.es.osaka-u.ac.jp/~masutani/Opamp/node12.html

 

#37: 等価変換

簡単のため，ディジタルフィルタについて述べます．ディジタルフィルタはインパルス応答が有限長の FIR フィルタと無限長の IIR フィルタに大別されます．前者の伝達関数は ｚ^-1 の多項式，後者の伝達関数は ｚ^-1 の有理式で表されますが，伝達関数が等しくても構成はいろいろ考えられます．FIR フィルタは直接型，IIR フィルタは縦続型が多いようです．

補足：アナログフィルタの構成法は数十年の検討を経て洗練されていますので，基本的な帯域制限用のディジタルフィルタの伝達関数は通常アナログフィルタの伝達関数の双1次変換から求めます．

[3-35] デジタルフィルタ
  http://www.ssc.pe.titech.ac.jp/lectures/SignalAndAnalysis/SignalsAndSystemsAnalysis12_050725.pdf
  直接型（Ⅰ，Ⅱ），縦続型，並列型，格子型
[3-36] 1 ディジタルフィルタ
  http://www-akaz.ist.osaka-u.ac.jp/~pak/lecture/HumanInfoProcessing/DigitalFilter.pdf
-------------------
[3-37] 双一次変換 - Wikipedia
  http://ja.wikipedia.org/wiki/%E5%8F%8C%E4%B8%80%E6%AC%A1%E5%A4%89%E6%8F%9B

 

ディジタルフィルタ (3)

sys.pdf sys-s.pdf sys.txt 記事一覧

直交２平面による伝達関数の表示（by 吉田成利）

#34: インパルス応答

線形時不変な回路の出力信号は（アナログの場合も，ディジタルの場合も）入力信号とインパルス応答の畳み込みで表わせます．インパルス応答とは単位インパルスを入力したときの出力のことですが，単位インパルスの定義はアナログとディジタルでかなり違います．アナログの単位インパルスは通常の関数としては扱いきれない超関数として定義されるので，sys.pdf ではステップ応答の微分として説明します．

[3-20] インパルス応答とたたみ込み
  http://www2.ic.sie.dendai.ac.jp/digital/%E8%AC%9B%E7%BE%A98.pdf
[3-21]  第 3 章：ダイナミカルシステムの 過渡応答と安定性
  http://k-lab.e.ishikawa-nct.ac.jp/course/CE1/10CE1/handouts/10CE1_lect05/10CE1_lect05_slide.pdf
[3-22] インパルス応答 - Wikipedia
  http://ja.wikipedia.org/wiki/%E3%82%A4%E3%83%B3%E3%83%91%E3%83%AB%E3%82%B9%E5%BF%9C%E7%AD%94
[3-23] 畳み込み - Wikipedia
  http://ja.wikipedia.org/wiki/%E7%95%B3%E3%81%BF%E8%BE%BC%E3%81%BF
  http://en.wikipedia.org/wiki/Convolution
---------------------
[3-24] ディラックのデルタ関数 - Wikipedia
  http://ja.wikipedia.org/wiki/%E3%83%87%E3%82%A3%E3%83%A9%E3%83%83%E3%82%AF%E3%81%AE%E3%83%87%E3%83%AB%E3%82%BF%E9%96%A2%E6%95%B0

 

#35: 伝達関数

アナログ信号の畳み込みはアナログ信号をラプラス変換したものの積になり，ディジタル信号の畳み込みはディジタル信号をｚ変換したものの積になります．畳み込みより積の方が計算しやすいので，回路の特性の解析や設計は，通常ラプラス変換したものやｚ変換したもので考えます．アナログの単位インパルスのラプラス変換，ディジタルの単位インパルスのｚ変換はいずれも１です．またインパルス応答のラプラス変換やｚ変換したものを伝達関数といいます．

入力の各標本値の絶対値が有限であれば出力の各標本値の絶対値も有限になる回路は安定であるといいます．線形時不変な回路が安定であるための必要十分条件はインパルス応答の標本値の絶対値の総和が有限であることです．線形時不変なアナログ回路の伝達関数の極がｓの右半平面内にあれば安定，ディジタル回路の伝達関数の極がｚ平面の単位円内にあれば安定です．

参考： 上図は吉田成利氏の在学中の作品で，アナログおよびディジタルフィルタの伝達関数の絶対値を複素数平面上で表示するプログラムです．同氏とは連絡がとれませんが，埋もれさせるには惜しい力作なので無断で紹介します．
  実行ファイル： http://pulsar.blog.ocn.ne.jp/IEICE/S-Yoshida.exe
  説明　　　　： http://pulsar.blog.ocn.ne.jp/IEICE/ET2001-55.pdf

[3-25] Scilab システム制御入門 伝達関数：概要
  http://alk.fam.cx/tfunc_010.html
[3-26] システムの伝達関数，システム応答 今週の授業の目的
  http://www.syscon.pse.tut.ac.jp/kisoHP/kougi03.pdf
[3-27] 伝達関数法 - Wikipedia
  http://ja.wikipedia.org/wiki/%E4%BC%9D%E9%81%94%E9%96%A2%E6%95%B0%E6%B3%95
  http://en.wikipedia.org/wiki/Transfer_function
--------------------------
[3-28] 第4章 伝達関数の回路表現
  http://jaco.ec.t.kanazawa-u.ac.jp/edu/digi/pdf/41.pdf
[3-29] 古典制御論 - Wikipedia
  http://ja.wikipedia.org/wiki/%E5%8F%A4%E5%85%B8%E5%88%B6%E5%BE%A1%E8%AB%96
[3-30] 線形システム論 ＞ 7.伝達関数
  http://stlabwww.ssi.ist.hokudai.ac.jp/yuhyama/lecture/linearsys/st6.ppt
  状態変数解析は sys.pdf 第5章で扱います．

ベストヒント

記事一覧

ANo.1の一部

OKWave「数学」の QNo.6885620（解決済み）：
微分方程式の問題 xy'=y^2 -1 の答えに至るまでの過程を教えてください。

ANo.1: 隙の無い模範解答

ANo.2: この問題が「変数分離形」の一語で終らないとしたら、演習量が著しく不足しています。解答付きの易しい問題集でよく練習することが必要です。・・・

についての感想です．

ANo.1 は教師の説明というより，友達が「俺は解けるぞ」と示している感じ，ANo.2 は正論を述べているが，学力不足の生徒に対する思いやりか少ない教師の感じがします．折衷案として，ベストアンサーでなくベストヒントを示すのはいかがでしょうか．ベストヒントといえないかも知れませんが，例えば

(1) 変数分離形であることに着目し，まず x(y^2 - 1) ≠ 0 の場合について考え，f(y) y' = 1/x の形にする．
(2) ∫f(y)y'dx = ∫f(y)dy = ∫(1/x)dx だから，F'(y) = f(y) である F(y) を探す．
(3) F(y) = log |x| + log C = log C|x| から y = g(x) となる g(x) を求める．
(4) x(y^2 - 1) ＝ 0 の場合について考える．

を最初のヒントとし，F(y) の求め方が分からなければ，さらに部分分数への分解をヒントとして与える．
蛇足： f(y)dy = (1/x)dx でもいいのですが，全微分の説明が煩わしい．

この問題に限らず，コピペできる解答例よりも指針を （できれば段階的に） 示す回答の方に共感します．質問者に自分で計算させることが肝要だと思います．

 

ディジタルフィルタ (2)

sys.pdf sys-s.pdf sys.txt 記事一覧

[3-15] 収束領域

#32: 差分方程式

微分方程式の差分方程式による近似については，このブログの「微分方程式の近似 (0)～(6)」を参照してください．線形の場合は１階の陰的ルンゲ=クッタ法を用いるとエネルギーの保存／非保存は不変で，近似誤差を3次以上の微小量にできます．

予定： 非線形の場合も同様にモデル化できますが得られる差分方程式が解析的に解けないことが多いので，近似計算法について９月の電気関係学会 北陸支部 連合大会で共著者が発表します（NOLTA2011-8037はモデリングの話）．

[3-12] 差分法 - Wikipedia
  http://ja.wikipedia.org/wiki/%E5%B7%AE%E5%88%86%E6%B3%95
  オイラー法，陽解法，(陰解法，クランク・ニコルソン法)
[3-13] ルンゲ＝クッタ法 - Wikipedia
  http://ja.wikipedia.org/wiki/%E3%83%AB%E3%83%B3%E3%82%B2%EF%BC%9D%E3%82%AF%E3%83%83%E3%82%BF%E6%B3%95
------------------------
[3-14] Introduction to Symplectic Integrator
  http://www-cms.phys.s.u-tokyo.ac.jp/~naoki/CIPINTRO/SYMP/symp1.html
   

#33: z変換

漸化式のｚ変換については[3-16]等を見てください．逆ｚ変換の方法はいくつかありますが，通常は部分分数分解を用います．

参考：「部分分数分解」＝「部分分数展開」？（http://en.wikipedia.org/wiki/Partial_fraction）
In algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function. 在職中に使用した制御工学の教科書でも「部分分数分解 - Wikipedia」のように使い分けず「部分分数展開」でした．

発展： ｚ変換には片側ｚ変換と両側ｚ変換があり，単にｚ変換といえば前者を指します．後者の場合収束領域は円環状になります．

[3-15] Z変換 - Wikipedia
  http://ja.wikipedia.org/wiki/Z%E5%A4%89%E6%8F%9B
[3-16] Z変換(ディジタル信号処理)
  http://ufcpp.net/study/dsp/z.html
[3-17] II. z-変換 1 z-変換の定義と簡単な時系列のz-変換
  http://homepage.usask.ca/~kut594/jp/Hokkai_web/Jnotes/E_Z-TRANSF.pdf
------------------------
[3-18] z 変換
  http://www.mlab.ice.uec.ac.jp/mit/text/singou/Notes/10Slide-print-2x2.pdf
  両側ｚ変換，収束領域．
[3-19] 逆 z 変換
  http://www.mlab.ice.uec.ac.jp/mit/text/singou/Notes/11Slide-print-2x2.pdf
  留数定理，多重根

Java のプログラム (7)

記事一覧 P22: 二分探索木（7/13 仕様変更） //------------------------------------------- package chk; class Node { int data; // 重複無効 Node l, r; Node(int k){data = k; l = r = null;} } class TreeS { Node top; TreeS(int k) {top = new Node(k);} void search(int k){ Node p = top.r; while(p != null){ if(p.data < k) p = p.r; else if(p.data > k) p = p.l; else break; } if(p != null) System.out.println(k); else System.out.println("?"); } void insert(int k) { Node p, q; q = top; p = top.r; while(p != null){ q = p; if(p.data < k) p = p.r; else if(p.data > k) p = p.l; else return; // 重複無効化 } p = new Node(k); if(q.data < k || q == top) q.r = p; else if(q.data != k) q.l = p; } void delete(int k) { Node p, q1, q2, q3; q1 = top; p = q1.r; while(p.data != k){ q1 = p; if(p.data < k) p = p.r; else p = p.l; if(p == null) return; // k 不在 } if((p.l == null) || (p.r == null)){ if(p.l != null) q2 = p.l; else q2 = p.r; if(q1.l == p) q1.l = q2; else q1.r = q2; } else { q2 = p.r; q3 = q2; while(q3.l != null){ q2 = q3; q3 = q3.l; } p.data = q3.data; if(q3 == q2) p.r = q2.r; else q2.l = q3.r; } } void show(String s, Node p){ if(p == null) return; show(s+"L", p.l); System.out.println(s+": "+p.data); show(s+"R", p.r); } void show(){show(" ", top.r);} } public class Main { public static void main(String[] args) { TreeS t = new TreeS(0); t.insert(7); t.insert(3); t.insert(9); t.insert(2); t.insert(5); t.show(); t.search(3); t.delete(3); t.show(); t.search(3); t.insert(3); t.delete(5); t.show(); } } //-------------------------------------------

二分木はリストより少し複雑なデータ構造で，二分 探索木やヒープに使われますが，抽象クラスは後回 しにして，とりあえず P22 の基本クラス を考えま しょう． ・次章で TreeS クラスを変更して，TreeH とともに 抽象クラス Tree のサブクラスにします． show() は Tree で定義します． ・top はダミーです．top.data を二分木のデータの 最小値より小さくすれば insert() は少し簡単に なります． ・data は重複しない（データベースの主キーのよう な）ものを想定しています． ・q2 は q3 の親です．親を q1，子を q2 にして q3 を使わないコードは処理が分かりにくくなります． アルゴリズムは下記の資料をご覧下さい．少々余白 があるので，参考までに progC.pdf の擬似コードを 用いて，delete() の処理内容を示します． void delete(int k) { Node p, q1, q2, q3; ${ p.data == k となる Node を探す． このとき p の親を q1 で覚える．}$ if(${ p の子は１個以下 }$) ${ p の子があれば，q1 の子にする． }$ else ${ p.data の次に大きい q3.data を新しい p.data にして，リンクをつなぎ変える． }$ } ${p.data の次に大きい q3.data を新しい p.data にして，リンクをつなぎ変える． }$ = { q2=p.r; q3 = q2; while(q3.l != null){q2 = q3; q3 = q3.l;} if(q2 == q3) ${ q3 = q3.l; を実行しないときは p.r に左の子 が無いから p.r = q2.r とすればよい． }$ else ${ q3 に左の子が無いから q3.r を q2 に接続． }$ } //------------------------------------------- run: LL: 2 L: 3 LR: 5 : 7 R: 9 3 LL: 2 L: 5 : 7 R: 9 ? L: 2 LR: 3 : 7 R: 9 構築成功 (合計時間: 0 秒) //------------------------------------------- [2-9] 2分探索木 - Wikipedia   http://ja.wikipedia.org/wiki/2%E5%88%86%E6%8E%A2%E7%B4%A2%E6%9C%A8 [2-10] 平衡2分探索木 - Wikipedia   http://ja.wikipedia.org/wiki/%E5%B9%B3%E8%A1%A12%E5%88%86%E6%8E%A2%E7%B4%A2%E6%9C%A8 [2-11] プログラミング/13 - CourseWiki   http://rabbit.media.osaka-cu.ac.jp/course/index.php/%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0/13 [2-12] binary search tree   http://www.geocities.jp/h2fujimura/mutter/tree/binary-search-tree.html [2-13] Javaで二分探索木クラス作成 - 似非学問的な手記   http://d.hatena.ne.jp/g940425/20101211/1292088124 [2-14] 木(1) - クラスライブラリ応用   http://www.mlab.im.dendai.ac.jp/~hsaito/javalib/tree1.html [2-15] ジェネリックス - Java 入門   http://java.keicode.com/lang/generics.php