離散コサイン変換 (5)

sys.pdf sys-s.pdf 記事一覧

DIF アルゴリズム

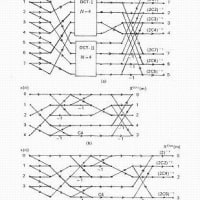
武部先生のゼミで教えて頂いた DCT-Ⅱ の時間間引き法を紹介します．参考資料は
  Rao and Yip, 安田 藤原 訳，画像符号化技術―DCTとその国際標準
  http://www.amazon.co.jp/%E7%94%BB%E5%83%8F%E7%AC%A6%E5%8F%B7%E5%8C%96%E6%8A%80%E8%A1%93%E2%80%95DCT%E3%81%A8%E3%81%9D%E3%81%AE%E5%9B%BD%E9%9A%9B%E6%A8%99%E6%BA%96-K-R-Rao/dp/4274034011
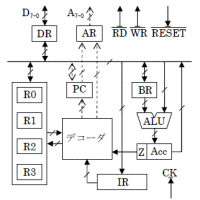
の 4.4節（上図は図4.5）です．これまでと同様に（両側）ｚ変換で考えてみましょう．

※ ｚ変換で考えてもあまり分かり易くなりませんでした --- どうして G(z)，H(z) を思いついたのか（esp.間引き後の後処理の見通し）推測できていません．以下は単なる備忘録です．

    X(z) = X₀(z²) + z^-1 X₁(z²)

に対して

    G(z) = X₀(z²) + z^-2 X₁(z²)
    H(z) = z^-1 X₀(z²) + z^-1 X₁(z²)

を考えると，G(z), z H(z) は z² の関数になり，標本化周期を２倍にできます．

    {X₀(z²) + z^-1 X₁(z²)}(1 + z^-1) = X(z) (1 + z^-1) = H(z) + G(z)

であり，x(n) の DCT-Ⅱ は z X(z^-2) + z^-1 X(z²) で考えるので

    z X(z^-2) + z^-1 X(z²) = z {H(z²) + G(z²)}

を時間間引きした DCT で計算できます．X(W^m)，X(W^N+m) を G(W^2m)，H(W^2m) の線形結合で求める計算は面倒ですが，線形結合の係数部分に現れる W^m は m の2進表示を用いると log₂ m 個の実数の積で表現できることから，変換行列が sparse だということは予想できそうです．