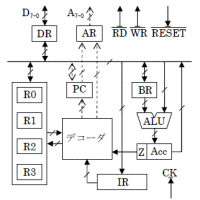
| sys.pdf sys-s.pdf 記事一覧 |
 高速フーリエ変換の原型 |
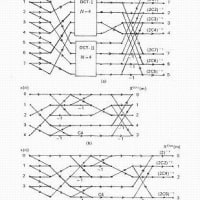
離散フーリエ変換の高速計算法である高速フーリエ変換の原理はz変換で考えると分かり易い[12].
{x0, x1, ・・・・・・ , xN-1} ( N = 2n )
の離散フーリエ変換を (DFTN X)(k) ( 0 ≦ k < N ) で表わすと,上記の式のように変形でき,0 ≦ k' < N/2 に対して
(DFTN X)(k') = (DFTN/2 X0)(k') + WNk (DFTN/2 X1)(k')
(DFTN X)(N/2 + k') = (DFTN/2 X0)(k') - WNk (DFTN/2 X1)(k')
となる.zに直接 WNk を代入して (DFTN X)(k) ( 0 ≦ k < N )を計算するときの乗算回数は (N - 1)2 であるが,(DFTN/2 X0)(k'), (DFTN/2 X1)(k') に分解すれば乗算回数は WNk との積を含めて との積を含めて 2(N/2 -1)2 + (N/2 - 1) に減少する.N = 2n としているので (n - 1) 段に分解でき,必要な乗算回数はほぼ nN に比例する.
蛇足: X0(z2) = X0,0(z4) + z-2 X0,1(z4), etc.
[10] 高速フーリエ変換 - Wikipedia
http://ja.wikipedia.org/wiki/%E9%AB%98%E9%80%9F%E3%83%95%E3%83%BC%E3%83%AA%E3%82%A8%E5%A4%89%E6%8F%9B
[11] 高速フーリエ変換(FFT) - 信州大学
http://laputa.cs.shinshu-u.ac.jp/~yizawa/InfSys1/basic/chap7/index.htm
[12] これなら分かる応用数学教室 ―最小二乗法からウェーブレットまで ...
http://www.kyoritsu-pub.co.jp/kenpon/bookDetail/9784320017382
pp.134-136










※コメント投稿者のブログIDはブログ作成者のみに通知されます