スペクトル分解とは (1)

sys.pdf sys-s.pdf 記事一覧 式の訂正： 2013-03-04

スペクトル分解定理 [7]

武部幹先生の信号処理ゼミに関する話題です．「スペクトル分解」が高校生向けの参考書でも使われているようなので，「スペクトル分解とは」等を Google で検索しました．以下は，工学系（付言すると非理学系）の学生諸君向けの補足ですが，ウソを書いているかも知れません．

(1) まず「スペクトル」とは何かを [0] で復習すると集合の各要素について，実数値で評価できる属性に着目し，その評価値の順に要素を並べたものと考えればよさそうです--- 分光スペクトルは光を波長順に並べる．
(2) 高校生が学ぶスペクトル分解は（当然ながら）行列の固有値分解で，「評価値の順に要素を並べたもの」というイメージは希薄です．
(3) 工学系の学生にとって難解なのは，関数解析で述べられている冒頭の式のような自己共役作用素 T のスペクトル分解です．[8] は [3] と [7] のつなぎとして掲げましたが，固有値の大きさに並べる意味は読み取れません．自己共役作用素は共役転置行列（エルミート行列）を一般化した概念であり，共役転置行列の固有値は実数で，異なる固有値の固有ベクトルが直交することは容易に証明できます．
※ 上図の式の E(λ) は射影行列を一般化した射影作用素で，[8] に合わせて x，y の内積を (y | x) で表わすと dE(λ) x = d(E(λ) x | x)．
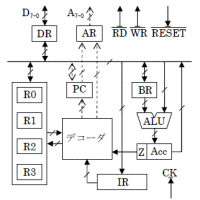
(4) １階の常微分方程式 x'(t) = A x(t) の x(t) ≠ 0 である解は |s I － A| = 0 の解を固有値とする固有関数です．A が線形時不変な回路の状態遷移行列のとき，対称行列やエルミート行列であることは期待できません．
※ A を対称成分と反対称成分に分解すると，反対称成分はエルミート行列の i = √(-1) 倍だから，対称成分を直交行列で，エルミート行列をユニタリ行列を用いて個別に対角化できます（0 でない非対角要素をもつ実対称行列はエルミート行列にならない）．x'(t) = A x(t) の解 x(t) = exp(A t) x(0) を展開して時間領域で計算するときに対角化できれば計算が簡単になります．しかし・・・・・

ここから無責任発言になります．
(5) 学生の (数学, 物理, 英語) の成績ベクトルを x = (x₁, x₂, x₃)^T, メーカ A 社の評価関数を 2 x₁² + 3 x₂² + x₃², 商社 B 社の評価関数を 2 x₁² + x₂² + 3 x₃², とします．これらの評価関数を x^T A x, x^T B x とおくと A = 2 P₁ + 3 P₂ + P₃, B = 2 P₁ + P₂ + 3 P₃ (P_i = e_i e_i^T, e_i は i 番目の要素が 1 の単位ベクトル) です．学生の成績スペクトルとして科目順の (2 x₁, 3 x₂, x₃), (2 x₁, x₂, 3 x₃) の棒グラフと，企業ごとに変わる (3 x₂, 2 x₁, x₃), (3 x₃, 2 x₁, x₂) の棒グラフのどちらが扱いやすいと思いますか？
※ 固有値分解をすべてスペクトル分解と呼ぶから紛らわしい（A社だけで考えるなら固有値の大きさで並べる方が実用的ですが）．
(6) 波長λの単位単色光 e_λ を入射したときの強度が (T e_λ, e_λ) = α_λ である色フィルタ（三原色分解用のどれか）に波長λでの分光スペクトル密度が u(λ) である光が入射したときの強度を固有値 α_λ の大きさの順に並べ替えたいと思いますか？ --- u(λ)はλの連続関数．
(7) インパルス応答が h(t) である線形時不変の回路に信号 x(t) を入力したときの出力 (T x)(t) は
    (T x)(t) = ∫x(t－τ) h(τ) dτ （積分範囲は (－∞, ∞) ）
だから，x(t) = exp(iωt) のときは (T x)(t) = x(t)∫x(－τ) h(τ) dτ = λx(t)，すなわち exp(iωt) は固有値λの固有ベクトルになっています．λ = H(iω) とおくと，実際の回路は実関数の入力 exp(iωt) ＋ exp(iωt) に対する出力 H(ω) exp(iωt) ＋ H(－ω) exp(iωt) も実関数なので，H(－iω) = H(iω)^*，すなわち T はエルミート作用素です．
※ H(iω) の関数表示が不明でも sin ω_kt を入力したときの出力 A_k sin(ω_kt + θ) の A_k，θ_k から H(iω_k) を計算でき，ナイキスト線図を描けます．なお，H(iω) はラプラス変換で求めた回路の伝達関数 H(s) の s に iω を代入したものに一致しています．
(8) 一般の（有限エネルギーの）実信号 x(t) は扱い難いので，まず周期が 2π/ω₀ の周期関数を考えます．このような信号の空間では各信号をフーリエ級数で厳密に表現できます --- 基底となるベクトルは可算個で exp(inω₀t)/√(π/ω₀) (－∞ < n < ∞)．
※ exp(±iωt)/√(π/ω) は固有値 －ω² の（２次元）固有空間の正規直交ベクトルです --- 固有空間は閉じていなければならない．
(9) (3) で述べた dE(λ) x = d(E(λ) x | x) はヒルベルト空間の作用素 T は ベクトル x に対する内積 (y_T | x) で表現できるという Riesz の定理に基づいています --- 内積の記法としては (x, y_T) や山括弧の〈x, y_T〉の方がよく使われます．基底が可算個のときは x = Σx_n e_n と展開できるので λ_n = (T e_n | e_n) とおくと
    (Tx | e_n) = (Σx_n T e_n | e_n) = Σx_n λ_n
すなわち Tx の e_n 成分は x の e_n 成分（フーリエ係数）と作用素 T のe_n に関する固有値（周波数伝達関数のフーリエ係数）の積になります --- おなじみの Y(iω) = H(iω) X(iω)．
(10) 電気工学では気楽に周期 2π/ω₀ の信号の空間に対して ω₀ → 0 とすればフーリエ級数がフーリエ積分になると説明しますが，数学ではこのような乱暴な推論は許されません．そもそも (－∞，∞) で三角関数を積分したときの収束性にしてもきちんと考えねばなりません．気楽にデルタ関数を使うのもご法度です（スティルチェス積分にする）．難しい議論は分かりませんが，関数の定義域を (－∞，∞) にすると，任意の実数 ω について (7) の exp(iωt) を考えることになり，(9) のような可算個の和でなく積分で表現することになります．冒頭の積分は λ の値を －∞ から ∞ まで変化させた形になっていますが「固有値の大きさの順に並べたい」という意思表示ではなく，「可算個の和で表現できないから積分を用いた」と考えればよいと思います．
(11) 冒頭の積分を直観的に理解するには濃淡画像を処理する空間フィルタを考える方が分かりやすいでしょう．空間フィルタの特性は２次元のフーリエ変換を用いて議論できます．時間波形の場合と同様に，空間周波数平面の１点が一つの固有関数に対応しています．各固有関数に対する作用素の固有値を３次元的に表現したものがスペクトル分解であって，空間周波数平面上での積分値を固有値の軸に射影した密度はほとんど使い道がありません --- 空間周波数平面上の（ルベーグ積分的な）２次元の等高線図による近似モデルでいえば，dE(λ) は x を隣接等高線で挟まれた部分に射影する作用素で，各λの値で x をどの辺に射影するかを示しています．

私見： 作用素に依存しないヒルベルト空間の固有ベクトル（高々可算個でもよい）順に並べて考えるのが本来のスペクトル分解であって，主成分分析等で行われるような主軸変換までスペクトル分解と呼ぶのは好ましくない --- 混乱を招くだけ！

[0] スペクトル - Wikipedia
  http://ja.wikipedia.org/wiki/%E3%82%B9%E3%83%9A%E3%82%AF%E3%83%88%E3%83%AB
[1] 固有値、固有ベクトル、スペクトル分解って何ですか？ 数学的な式よりも ...
  http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1340751313
  どなたか猿でもわかるように教えて下さい。
[2] スペクトル分解 | Funeral of vlack jack
  http://stupid-newbie.jugem.jp/?eid=505
[3] 大学入試問題 行列のスペクトル分解とそれに由来する - 数研出版
  http://www.chart.co.jp/subject/sugaku/suken_tsushin/72/72-6.pdf
[4] 演算子のスペクトル分解 - 京都大学OCWへようこそ
  http://ocw.kyoto-u.ac.jp/09-faculty-of-engineering-jp/quantum-theory-for-electrical-and-electronic-engineering/pdf/chap5.pdf
[5] 特異値分解 - Wikipedia
  http://ja.wikipedia.org/wiki/%E7%89%B9%E7%95%B0%E5%80%A4%E5%88%86%E8%A7%A3
  特異値分解は、行列に対するスペクトル分解定理の一般化とも考えられ、正方行列に限らず・・・
[6] 現代解析学基礎論第一講義ノート(pdf)
  http://matha.e-one.uec.ac.jp/~naito/06inkogi.pdf
  ※ 全部で 172 ページ．「4.3 スペクトル分解定理と(λE - A)^-1 の表現」
-----
[7] スペクトル分解定理
  http://www5d.biglobe.ne.jp/~pomath/study/spectrumresolution.pdf
  この怪しげな文書は Hilbert 空間 X 上のユニタリ作用素，自己共役作用素のスペクトル分解を１時間で復習・・・
  http://www5d.biglobe.ne.jp/~pomath/study/spectrumresolution2.pdf
[8] [5/17] 第3講 行列のスペクトル分解[pdf]
  http://www.math.s.chiba-u.ac.jp/~nagisa/lecture04/fa3.pdf
  行列が無限次元になると・・・その準備として行列の場合にも積分形の表示がどうなるかを・・・
[9] 関数解析入門2011 - Nagoya University
  http://www.math.nagoya-u.ac.jp/~yamagami/teaching/functional/hilbert2011.pdf
  ※ 全部で 100 ページ．「10. スペクトル分解定理」