角度が等しい

　また「教えて数学」からの問題。

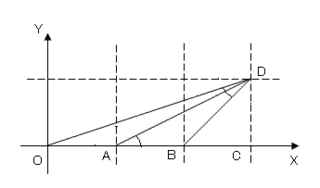
　上図において、∠ＯＤＢ＝∠ＢＡＤを証明せよ。
ただしＡ（１，０），Ｂ（２，０）、Ｃ（３，０）、Ｄ（３，１）とする。

　はて？　考えるのも面倒なので三角関数で解いてしまおう。
△ＡＣＤにおいてtan∠ＣＡＤ＝１／２。
　∠ＯＤＢ＝∠ＯＤＣ－∠ＢＤＣだから加法定理により
tan∠ＯＤＢ＝tan（∠ＯＤＣ－∠ＢＤＣ）
　　＝（tan∠ＯＤＣ－tan∠ＢＤＣ)／（１＋tan∠ＯＤＣtan∠ＢＤＣ)
　tan∠ＯＤＣ＝３、tan∠ＢＤＣ＝１だから
tan∠ＯＤＢ＝（３－１)／（１＋３・１)＝２／４＝１／２
∴tan∠ＯＤＢ＝tan∠ＣＡＤ（＝tan∠ＢＡＤ）

∠ＯＤＢも∠ＢＡＤも鋭角なので∠ＯＤＡ＝∠ＢＡＤ　（証明おわり）

めでたし、めでたしと思ったら、これは中学生むけの問題とのこと。　
むむ、困った。三角関数を使えない。

模範解答（？）
　△ＯＤＡと△ＤＡＢの相似を示す。
　ＯＢ：ＢＤ＝２：√２＝√２：１
　ＤＢ：ＢＡ＝√２：１
　∠ＯＢＤ＝∠ＤＢＡ
　以上より２辺の比とその間の角度が等しいので△ＯＤＡ∽△ＤＡＢ
　∴∠ＯＤＡ＝∠ＢＡＤ　（証明おわり）