定期券

　先日、名古屋市交通局の「虎の巻～定期券編～」を地下鉄の某駅で手に入れた。これを見ていたら、私の知らないことが結構載っていた。

　最大の発見は、同じ駅を２度とおらない一筆書きなら、どこを経由するモノでも買えるということだ（注．ただし経路が長いとそれなりの料金になる）。以前、これに近い（そのものだったかも）定期券を買おうとしたら、「それはダメ。どうしてもというなら全線定期を」といわれたことがある。

　そして２番目。通勤定期は、自宅の最寄駅～勤務先の最寄り駅までしか買えないと思っていた。大阪に住んでいた頃だと思うが「区間が同じだからココまで買わせてくれ」といって断られた経験がある。こんなことが名古屋市交通局では許されるのだ。そういえば、定期券の購入申込書から勤務先の住所を書く欄がいつの間にか消えている。なんとか定期を買ってもらおうという努力が感じられる。

　私は、仕事場から更に４駅さきにあるマンガ喫茶に毎週行く。その交通費＋仕事場までの定期にあと約３０００円たせば全線定期が買える。こうすれば地下鉄のあるところならどこでも行けるから有利だと思い、全線定期を買っていた。実際、全線定期の料金１４５８０円の５０％以上は余分に乗っていたし、多い月は＋１００％近く乗っていたこともある。

　だが上記発見によりマンガ喫茶まで定期（３区）を買うことができるので、安上がりになる。「それでも５割以上余分に乗るなら全線の方が得では？」という意見もありそうだが、実はその経路から外れて乗ることは月に２回程度しかない。その都度、ユリカなどを使った方が安いのだ。

４回目の来場

　この日は火曜日。トヨタ館が狙いで行った（らしい）。この日からサマータイムで開場時間が早くなり、９：１５に入場。整理券を受け取った後、ワンダーサーカス電力館へ。ここは行列が短めなのがいい。子供向けかと思いきや、結構たのしめる。立体的にコースが配置されたライドが凝っている。

　そこから遊びと参加ゾーン（写真）へ。フミコとコイデは無くなっていた。
　この写真は後日、ファミリー愛ランドの観覧車から撮ったものだ。左奥はわんぱく宝島。右に見えるのは地球市民村。この日もアースドリーミングシアターで休憩した。なお、手前に見えるのはレストランと休憩所。

　そこからグローバルコモン６のラオス館とオーストラリア館へ。ここでワニロールを食べる。1100円。

　なおも時間があるので愛・地球広場で休憩。そしてやっとトヨタ館。猜疑心の強い私は、本当にロボットがトランペットを吹いているのか疑ってしまった。

（どうもこの日の記録は順番が怪しい。記録によればオーストラリア館が最後になっている。だがラオス館に行っただけでトヨタ館に行ってオーストラリア館にとんぼ返りするとは考えにくい。トヨタ館のスケジュールの結果、そうなることもあり得るが、そうすると昼食が遅すぎる）

　この日の歩数は15750歩。前回に引き続き少ないが、行ったりきたりした分、前回より多い。

３回目の来場

　一日おいて今日も入場。行った理由は万博の番組で見たフミコとコイデらしい。これは人が乗って足で漕ぐと進む２頭のロボットマンモスだ。

　９：４５ごろ北ゲートから入って、まずは三井東芝館へ。３時間待ちが当たり前の人気施設だが、この頃は大して並ぶこともなく入れた。ここは、自分の顔をスキャンしてグランオデッセイというＣＧアニメに自分を出演させることができるフューチャーキャストシステムが目玉だ。自分を探すのに少し苦労したが、なかなか面白い映像だった。ブレイン、オーソリティ、ガーディアン、レシーバーという４つの役のうち、確か自分はブレインだったと思う。そして「ヘぇー」というエンディング。（今はハウステンボスにあるんですな。知らんかった。）

　そして「遊びと参加ゾーン」へ。この辺の記録・記憶が曖昧なのだが、わんぱく宝島のロボットステーションに入ったらしい。ここでは恐竜の２足歩行ロボットに会える。

それから地球市民村へ。ここにはアースドリーミングシアターという、寝転んで見ることができるシアターがある。コレは格好の休憩所で、のちのち穴場となる。また、ここのアテンダントのコスチュームが私のお気に入りだ（写真）。

　そしてモリゾーキッコロメッセ（モリコロメッセ）へ。ここでモリゾ－とキッコロに遭遇した。会えない人は中々会えないらしいが、私は探していた訳でもないのに、あっさり会えた。

　そしてようやくフミコとコイデにあった（写真左が母のフミコ。右が息子のコイデ）。実によくできている。前後に歩いて鼻も動く。本当は乗りたかったのだが、恥ずかしくて遠慮した。

　ここで食事をしたらしい。プルコギ丼８００円。この頃は平日だったせいもあってか人が少なかった。あっさり注文して好きな席で食べることができた。「愛知万博、大丈夫か?」と思ってしまった。

　それからＪＲ東海館のリニアモーターカーの中に入って帰ってきた。シアターもあるのだが、こちらは行列が長めだったので後日。

　この日の歩数は13550歩。いろいろ行ったにしては少ない。会場に慣れてきて、ほぼ最短距離で移動したから？

２回目の来場

　ようやく２回目の万博会場。あとから考えれば、もっと頻繁に行けばよかったんだけど、株取引をしているから、消極的になったのだろう（自分のことながら今となっては本当の理由を忘れてしまった）。かといって週末はそれなりに混雑するので平日ねらいだ。

　当時のメモによると、マンモス観覧（グローバルハウス：ＧＨ）の予約が取れたことが行った理由らしい。パソコンで予約を取った記憶がある。この日は９：５０に西ゲートから入った（オープニングベルは録画して後で見たらしい）。ただし入場してすぐにＧＨに行ったのではなく、長久手日本館に行ったらしい。ここの売りは３６０°全天球型の映像が楽しめる「地球の部屋」。でも私はそれよりも、日本の時代の流れを懐かしの電化製品などと共に展示したブースが気に入った。

　それからワールドレストラン（愛地球広場の脇にあった食事スペース）で石焼きビビンバを食べた。1300円。ここは後日にもお世話になるのだが、見た目と違って中々美味しい。
　そしてやっとＧＨ（オレンジ）。月の石やトゥマイの頭骨も見た。ユカギルマンモスは意外と小さい印象。

　帰るにはまだ早いので、前回いかなかったグローバルコモン４へ。ここでアイルランド館とイギリス館に入っている。この近くにはロシア館があって、マンモスの骨格やスペースシャトルなど魅力的な展示があったのだが、行列が長めで敬遠した。

　この日の歩数は19800歩。前回とほぼ同じ。

メガマフィン

　先週、メガマフィンを食べてきた。以前、「ソーセージマフィンは好きだがソーセージエッグマフィンは嫌い」と書いた。ではメガマフィンはどうか。

　答えは「Good」。やはりソーセージが２枚ということで、タマゴに勝った感じだ。カロリーが気になるので、ポテトは無し。次回も食べよう。毎週はきついので来週だ。でも期間限定だから、その頃には無いかも。

WINDOWSのゲーム

　1ヶ月ほど前からフリーセルがｍｙブームになっている。以前にもブームはあったのだがここ数年は主にハーツをやっていた。そのせいもあって、フリーセルはルールすら忘れていた。

　なぜまた始めたかと言うと、某ラジオを聴いていたら「妻がフリーセルばかりして困る。ちゃんと仕事をしてくれ」と言う一般参加者のおじさんが出てきたからだ。いいなぁ、フリーセルに夢中になるおばちゃん。パチンコや韓国ドラマにいれこむおばさんより好きだぞ。

　どうみても無理に見えるカードの山がキレイになくなるのが気持ちいい。上図に示した#25392のようなのがキレイになくなる。でもこのブームもいずれ去るんだろう。そしてルールも忘れてしまうんだろう、以前のように。

大翼竜展

　世界最大の翼竜展に行ってきました。ケツァルコアトルスのデカさに仰天したけれど、翼竜といえばプテラノドン（写真）でしょう。
複製ではなく実物化石が多かったのが嬉しかった。

　私は恐竜の名前の意味に興味がある。バリオニクスが「重い爪」、アロサウルスが「ちがうトカゲ」、ベロキラプトルが「すばしこい泥棒」、などなど。翼竜は恐竜じゃないけど、興味深く見せてもらった。プテラノドンが「歯のない翼」という意味だとは知らなかった。

　オマケ的な展示だったワタリアホウドリの大きさにも驚いた。

朝定食

　先日、マンガ喫茶Ｋに行ってきた。初めて朝の定食を食べてみたが、中々いい。見た目、吉野家の特朝定食だが、特朝定食４９０円より少し安い。シャケが小さめだが、十分だ。味噌汁の味は改善の余地ありだ。

　※万博の話題が途切れているが、実は次に行ったのは２０日だ。だからしばらくその話題は扱わない予定だ。最終月を除き、なぜか月の前半はあまり行っていない。

頭の体操

以前にも書いたが、教えてgooに出てくる数学の問題をときどき解いて頭の体操をしている。
私の興味を引くのは、難しい問題よりも、易しそうなのに意外と苦労するとか、エレガントな回答がある問題が多い。

問．図に示す平行四辺形ＡＢＣＤで、ＥＦ//ＡＣのとき、△ＡＥＤ＝△ＣＦＤを証明せよ。

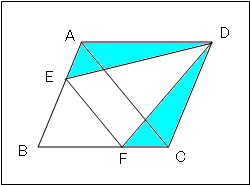
私には「へぇー、そうなの？」って感じの問題だ。

幾何に限らず、ひらめきを要する問題は難しい。
ひらめくのは諦め、ベクトルを使ってガシガシ解くことにした。

→ＡＢ＝→ａ、→ＡＤ＝→ｂとし、→ＡＥ＝ｓ→ａ、→ＡＦ＝→ａ＋ｔ→ｂとする（ｓ、ｔ は定数）。
ＥＦ//ＡＣは　　（→ａ＋ｔ→ｂ）－ｓ→ａ＝ｋ（→ａ＋→ｂ）
と表せる。
整理すると　　　（１－ｓ）→ａ＋ｔ→ｂ＝　ｋ→ａ＋ｋ→ｂ
係数を比較すれば　　　　　　１－ｓ＝ｔ　　・・・（＊）
ここで展望。∠ＥＡＤ＝∠ＦＣＤなので、→ＡＥと→ＡＤの内積が、→ＣＦと→ＣＤの内積に等しければ△ＡＥＤ＝△ＣＦＤが言える。
→ＡＥ・→ＡＤ＝ｓ→ａ・→ｂ
→ＣＦ・→ＣＤ＝（→ＡＦ－→ＡＣ）・→ＣＤ
　　　　　　　＝｛（→ａ＋ｔ→ｂ）－（→ａ＋→ｂ）｝・（－→ａ）
　　　　　　　＝（１－ｔ）→ａ・→ｂ
（＊）より　　＝｛１－（１－ｓ）｝→ａ・→ｂ
　　　　　　　＝ｓ→ａ・→ｂ
∴→ＡＥ・→ＡＤ＝→ＣＦ・→ＣＤ
両辺をｃｏｓ∠ＥＡＤで割り、ｓｉｎ∠ＥＡＤをかけ、１／２にすれば
　　△ＡＥＤ＝△ＣＦＤ　（証明おわり）

いちおう解けたが、エレガントとは言いがたい。それに中学生にこの解法は無理だ。
中学生むけの解等が次だ（一回答者のヒントに基いた）。


上図のように対角線ＤＢを引く。
△ＣＢＤにおいて、△ＦＤＣ：△ＢＤＦ＝ＦＣ：ＢＦ
同様に△ＡＢＤにおいて、△ＡＤＥ：△ＥＤＢ＝ＡＥ：ＥＢ
四角形ＡＢＣＤは平行四辺形なので　△ＣＢＤ＝△ＡＢＤ
ＥＦ//ＡＣより　ＦＣ：ＢＦ＝ＡＥ：ＥＢ
以上より　、△ＡＥＤ＝△ＣＦＤ

うーん、エレガント。ベクトルなんて道具を手に入れちゃうと、ピュアな感性が汚れていくのか。

昨日の追記

　昨日の記事で、愛知万博へは仕事場から行ったのだが、仕事場でキー綴じ込みをしてしまった。本来なら万博会場から仕事場に戻ってクロージングベルなどを見たかったのだが、家に帰る羽目になった（合鍵は家にある）。だが、そのまま帰るには早いので、前に書いたマンガ喫茶Ｆに行った。この後、間もなくＦは閉店してしまい、これがＦに行った最後となった。

　この時は、まさか閉店するとは思わなかった。普段は週末の朝に行っていたので、「夕方はこんな客層なんだ」と雰囲気を楽しんでいた。頼んだメニューはホットコーヒー。３１０円（たぶん価格３６０円に割引券５０円）。後日、閉店を知ったときは落胆したが、愛知万博が無かったら、この日に行くことはなかった。