ジュニア数学オリンピックの簡単な問題（１１４）

こんにちは。東久留米市の学習塾塾長です。

雲が少ない青空で陽射しは強いのですが、ときどき冷たい風がピューピューと鋭い音を立てて、冷え込みの厳しい日になりました。外出の際は、厚手の外套を着て暖かくしましょう。

さて、今回は２０１７年ジュニア数学オリンピック予選に出題された場合の数の問題を取り上げます。

問題は、
「３×３のマス目の各マスに、１以上９以下の相異なる整数を１つずつ書き込む方法であって、次の条件をみたすものは何通りあるか。

　●マス目の各行に書かれている３個の整数の中で、１番右のマスに書かれている整数が最大であり、１番左のマスに書かれている整数が最小である。

　●マス目の１番左の列に書かれている３個の整数の中で、１番上のマスに書かれている整数が最大であり、１番下のマスに書かれている整数が最小である。」

▲問題図

です。

早速、取り掛かりましょう。

まず図１のように、３×３のマス目の各マスをＡから Ｉ としましょう。

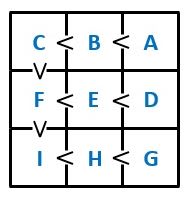
▲図１．各マスをＡから Ｉ としました

図２のように、Ｉ は１から９の整数の中で最小なので、１になります。

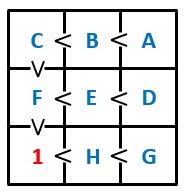
▲図２．Ｉ は１です

次に、Ｆを調べましょう。

Ｆより大きい整数は、少なくともＡ、Ｂ、Ｃ、Ｄ、Ｅの５個はありますから、Ｆが取り得る整数は、２、３、４になります。そこで、Ｆについて場合分けして調べていきましょう。

・Ｆが２の場合
図３のように、Ｃ＜Ｂ＜Ａ、Ｅ＜Ｄ、Ｈ＜Ｇの３つの大小関係になる整数の組合せを作ればＯＫです。

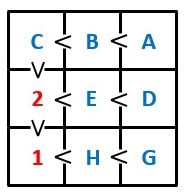
▲図３．Ｆが２の場合です

そこで、３から９までの７個の整数を３つのグループ（各グループの要素の個数は３、２、２個）に分け、それぞれのグループの整数を大きい順に、Ａ、Ｂ、Ｃと、Ｄ、Ｅと、Ｇ、Ｈとすれば条件を満たすＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｇ、Ｈを決めることができます。

そして、このような３つのグループの分け方は、
7Ｃ3×4Ｃ2×2Ｃ2＝７×６×５/（３×２×１）×４×３/（２×１）×２×１/（２×１）＝２１０通り
です。

・Ｆが３の場合
図４のようにＦが３の場合、Ｈは２で、あとはＣ＜Ｂ＜Ａ、Ｅ＜Ｄの２つの大小関係になる整数の組合せを作ればＯＫです。

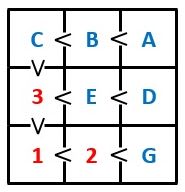
▲図４．Ｆが３の場合、Ｈは２になります

そこで、Ｆが２の場合と同じように、４から９までの６個の整数の３つのグループ（各グループの要素の個数は３、２、１個）への分け方を計算すると、
6Ｃ3×3Ｃ2×1Ｃ1＝６×５×４/（３×２×１）×３×２/（２×１）×１/１＝６０通り
です。

・Ｆが４の場合
図５のように、Ｆが４の場合、Ｈは２、Ｇは３で、あとはＣ＜Ｂ＜Ａ、Ｅ＜Ｄの２つの大小関係になる整数の組合せを作ればＯＫです。

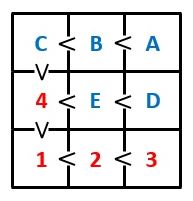
▲図５．Ｆが４の場合、Ｈは２、Ｇは３になります

そこで、Ｆが２、３の場合と同じように、５から９までの５個の整数の２つのグループ（各グループの要素の個数は３、２個）への分け方を計算すると、
5Ｃ3×2Ｃ2＝５×４×３/（３×２×１）×２×１/（２×１）＝１０通り
です。

以上から、条件を満たす書き込み方法は、
２１０＋６０＋１０＝２８０ 通り
で、これが答えです。


簡単な問題です。