なんで三角関数なんて習うんだろう？（その３）『度とラジアン2』

えーと、度(以下、degreeまたはdegとする）とラジアン（以下rad）の安直説明の続き。

まずは角度とはなにか？

iPhoneアプリの大辞泉によれば、『二つの直線や平面が交わって作る角の大きさ』とある。　理化学辞典でも引いてみたが、角度の説明は無かった。

『直線や平面』となっているが、『曲線や曲面』が交わっても角度は定義できる。　これは付けたし。

それから、普通あまり意識しないと思うが、角度はベクトル量である。　大きさだけでなく、方向もある。　X-Yの直交座標系（つまりはグラフ用紙のこと）で横軸にX軸を取って、左から右に向かってプラス方向とし、縦軸にY軸をとって、下から上に向かってプラス方向とすると、一般的には反時計周り方向に角度のプラス方向とし、時計周り方向をマイナス方向とする（下図参照）。　これは、証明されるものではなくて、こう決めたという『定義』である。　こうすると何かと便利なのである。


なお、上図ではX軸から角度を取っているが、向きについてはどこからはじめても反時計周りをプラス、時計回りをマイナスにする。　始点がどこでも良いということ。　

さて、degreeでは円を一周した角度が360degで、それを360等分した角度が1degとなる。1degを高速道路とかの登りの角度で言うと1.75%に相当する。　直角は360degの1/4なので、良く知ってる90degとなる。　これが度（degree）。

一方、同じ角度でもラジアンの定義は下図を見てもらわないと思い出してもらえないかもしれない。



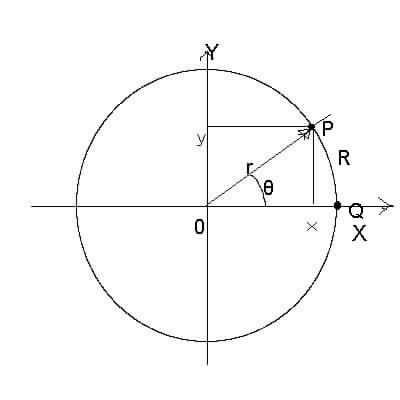
X－Y直交座標系（しつこい言い方だが、数学や物理にとって座標系を定義するというのは非常に重要なことなのだ）において、原点O（ゼロでなくてオー）の周りに半径ｒ（あえて小文字のアールにしています）の円をかいて、円とX軸の交点Qから角度θの円周上の点Pを置いたとき、点Qから点Pまでの円弧の長さをR（このアールはあえて大文字でR、円弧の長さとは扇形の周の長さと言う意味）としたときに、
θ＝R/r
がラジアンの定義となる。

小学校で、円の周の長さは
＜周の長さ＞＝２×＜円周率＞×＜半径＞、
中学校では
＜円周の長さ＞＝2πr
と習うはずであるが、円を一周すると周長は2πrなので、このときの角度θは
θ＝R/r＝2πr/r=2π
となる。
半周なら、
θ＝πr/r＝π
である。
もちろん、π＝3.141592......のこと。

ここまでは、degとradの定義上の話。　

degをradに直すには
θ(deg)→θ×(2π)/360
とすれば変換できる。
θ(deg)→θ×(π)/180
としても良い。

エクセルで=sin( ),=cos( ),tan( )の(　）の中には上記のようにして角度を入力しないといけない。　関数電卓では、いちいちそんな面倒なことをしたくないので、普通はdeg,radのどちらかで計算するための切り替えができるようになっている。

Windowsのアクセサリに電卓があるのは多くの人が知っていると思うが、表示切替で関数電卓にできる。　その関数電卓にもdegとradの切り替えボタンがある。

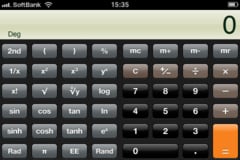
下の図はiPhoneのデフォルトの電卓であるが、左下に『rad』のボタンがあり、数字の表示のところに『deg』の文字がある。　今はdegモードで、radボタンを押すとradモードになる。


なんで、ラジアンなんて単位を数学や物理で使うのか？　それは、上記の角度の定義の仕方の違いによる。

Wilipediaに書かれている角度の定義の由来が本当かどうかわからないが、degreeとは人義的な角度の定義なのである。　円を一周した角度が360にしようと100にしようとどうでもいいのである。現代はほとんどの数字が十進数でかかれるので、今角度の単位を決めるなら、円を一周したときは１００とか１０００にするだろう。　でも、古代は12進数とか60進数とかが一般的であったから、12でも60でも割り切れる360と言う数字は便利であったのであろう。

一方、ラジアンは上記のように＜円弧の長さ＞÷＜半径＞で定義される。　この定義の良いところは、長さと言う人義的で無い物理的な量を基に定義されることにある。　さらに、単位系にもよらない。　＜円弧の長さ＞と＜半径＞の単位がメートル（ミリメートルやキロメートルも含んで）だろうとインチであろうと、尺であろうと同じ単位なら、ラジアンで表した場合の角度は変わらない。

日本では国際的に一般的なSI単位系（メートルｍ、キログラムkg、セカンド＝秒sec、アンペアA）を使うことに法律（計量法）で定められている。　そして、SI単位系で使われる角度単位がラジアンであり、ラジアンは＜メートル＞÷＜メートル＞の代わりに使われる単位なのである。　ちなみに、アメリカは未だにポンド－インチ単位系をつかってるので、ラジアンも＜インチ＞÷＜インチ＞である。　でもradの値は変わらないのである。

ここまでは一般論である。

でもラジアンが物理や数学で常用されるのには、実利的な理由がある。

少し話しが発展してしまうが、読み飛ばして頂きたい。

高校の数学で習っているはずであるが、
sin(x)の一階微分はcos(x)である。



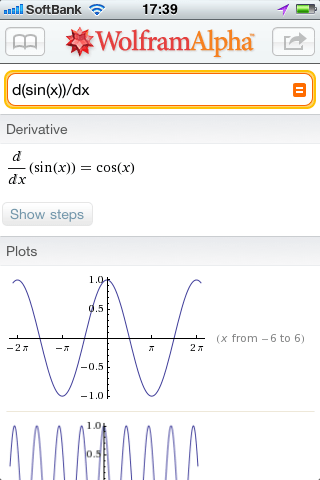
この関係を使うと、x=0で、
sin(X)の傾きは1となる。

さらに、これは、物理で多用される方法なのだが、角度をラジアンで表して、
θが１より十分に小さいときを考える（θ<<１と普通書く）とすると、
θはほとんどsin(θ）と同じ値となる。　傾きが１なのだから当然である。

具体的に見てみよう。θをdegreeで1degとすると、
θ＝1deg=1×π/180(rad)=0.0174532(rad)
一方、
sin(1deg)=0.017452
となる。　よって、radでθ<<1なら、
θ＝sin(θ）
と置き換えできるのである。

ここで、一つ物理的に重要なことがある。

θもsin(θ）も＜長さ＞÷＜長さ＞の量であるということである。　物理的には幾ら数値が近くても、その値が別の量であると同じものとして扱うことはできない。　専門的には『物理量の次元が異なる』と言う。　この事は、強調しておかなければいけないことである。　

この置き換えの最も基本的な応用が、いわゆる単振り子の運動である。


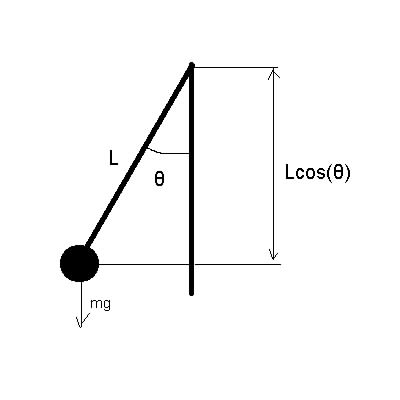
振り子に働く力が重力mg（mは錘の質量、gは重力加速度）だけならば、振り子の運動方程式（微分方程式）は、

θ"+(g/L)sin(θ)=0

となる。　Lは振り子の長さである。　この微分方程式の答えは簡単に求まらない。　なぜなら、sin(θ）の取り扱いが面倒だからである（数学的には非線形だからと言う）。

ここで、θがラジアンのときにθ<<1の場合なら、θ＝sin(θ）の関係を使って、
θ"+(g/L)θ=0
と言う式にすることが出来る。

この微分方程式は簡単に解ける。　そして、振り子は一定の周期Ｔでゆれる。　Tは下の式で決まる。

Ｔ＝２π√(L/g)

これは、小学校と中学校で習う振り子のゆれる周期は錘の質量mに依存せずに、振り子の長さLだけで決まるという、ガリレオが発見した振り子の等時性のことを式で表したことになる。

つまり、振り子の等時性はラジアンで表した角度θが１(≒57.3deg)よりも十分に小さいときのみ成立する関係である。

上記の微分方程式の角度の単位をdegreeで表現すると、どうしたら良いか、私には想像がつかない。

degreeは小学校から習うので非常に身近な単位なのであるが、数学や物理で扱うにはラジアンの方が便利なのである。

ちなみに、ガリレオが振り子の等時性を発見したときには微分・積分が無かったため、上記のような数学的な証明はなされていない。　あくまで、経験と観察に基づくものである。　また、角度変化が非常に大きい振り子の運動を数学的に扱うためには、かなり複雑な手順が必要である。　まぁ、今なら数値計算してしまうが。

度とラジアンの使い方の違いについて、何となくでも分かってもらえたであろうか？