なんで三角関数なんて習うんだろう（その４）

このテーマ、『なんで習うんだろう？』と言う答えを簡単に出せずにいる。　なぜなら、余りに身近すぎて、『なんで？』なんて思ったことが無いから。

で、今回も答えを出せずに、回り道。

例によって、直交座標系と円の図を使って。



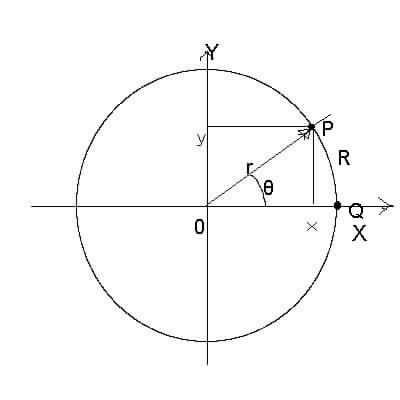
三角関数を幾何学の範疇で考えていると、その応用は非常に狭い。

でも、上の図で、X軸からの角度θで長さｒの線分Ｏ－Ｐを考えると、点ＰのＸ座標は
x=ｒcos（θ）、
Y座標は、
y=rsin(θ）
つまり、点Pの座標(x,y)は、

(x,y)=r(cos(θ),sin(θ)）

となる。

直角三角形で考えるなら、斜辺はO-Pの長さｒで、底辺はｒcos（θ）、高さはrsin(θ）である。

O-Pの傾きはsin(θ)/cos(θ）＝tan(θ）となる。

こう考えると、中学校で習う一次関数、
y=ax+bのaとはtan(θ）であるということである。

この関係は、高速道路や山道の標識によくある傾斜5%とかある、5%とはtan(θ)のことを意味している。　100m前進するのに5m昇るという事だ。

ちなみに、上の図でO-Pの線分ｒが一定で、θをぐるっと一周させると円が描けることになる。　楕円はｒもθも変化する。

さて、角度θが一定の速さで変化していると考えてみる。　たとえば、1秒間に360度つまり2π(rad)の角度が変化するとすると、角度の変化する速さは
2π(rad)/1secとなる。　1秒間に何回θがまわるかを周波数と呼び、普通ｆ(英語のfrequencyの頭文字）で表す。　また、1秒間に変化する角度を角速度といって、普通ギリシャ文字のω（オメガの小文字）で表し、

ω＝2πｆ(単位はrad/sec)

の関係となる。　f=1　ω＝2πで上の関係と同じである。

ここまで書いてくると、色々と書きたくなる。　

最近は余り使われなくなったが、ギターの弦のチューニングに20年以上前までは音叉が一般的に使われていた。　ギターの５弦（上から二本目の太い弦）開放弦（つまりどのフレットも抑えていない状態）の音の高さをAの音（ドレミで言えばラの音）に合わせるのだが、その基準に１秒間に４４０回振動する音叉（ｆが440ヘルツ＝Hz)を使っていた。　最近はチューナーが安くなったので、初心者も音叉なんて使わずにチューナーでチューニングするであろうが、５弦の開放弦は440Hzに合わせるようになっている。

とすると、ω＝２πｆ　の関係を使うと、440ヘルツということは、
ω＝２πかける４４０　の角速度と言うことになる。　ここで、ωの単位はrad/secである。　周波数ｆの単位が1/secなのだ。

この辺りのことを何となく分かろうとすると、上の図が頭の中にあると分かり易いことになる。

ちょっと、一気に飛ばし過ぎたかも知れない。　

三角関数はあと数回続けるつもりである。