二次方程式の話2（大人の数学・物理補習塾）

はじめに、以下にWolframAlphaのプリントスクリーンがいくつも出てくるが、Inputとなっている式だけを見て頂きたい。

サスペンションとは良く言った物で、自動車の車体は空中にサスペンドされている（日本語なら吊られている）。　吊られているというと、上から紐で吊られているイメージになるので、なんとなく車体が吊られているというのは分かりにくい。　それなので、敢えて英語のサスペンド（suspend)されているということにする。ちなみに、サスペンスドラマやサスペンス映画と言うものがあるが、このサスペンスとは気分が不安な状態にされるということで、動詞なら同じサスペンドである。気分が落ちついていない状態にあるということだ。　サスペンドのもう一つの名詞形がサスペンションである。　これは日本語に直すと懸架装置となる。

サスペンションの役割はいくつかあるのであるが、最も基本的な役割は、車体（及び車体に乗っているもの＝エンジンやトランスミッション、人、荷物）を路面がデコボコしていてもそのデコボコが車体に伝わらないようにすることにある。　遠めから走っている車を見たときに、タイヤは上下に動くのだが、車体は一定の高さを維持することが理想である。　サスペンションが無い（＝荷物を運ぶのに使う台車がそうである）と路面のデコボコに応じて車体もガタガタすることになる。　台車で物を運ぶときに、アスファルト舗装された路面でも台車に乗せた荷物がガタカガとする経験は多くの人があると思う。　でも、同じ路面を自動車で走っても、ガタガタはほとんど気にならないはずである。　それは、そう言う風にサスペンションが設計されているからである。

では、それをどうやって設計するか？　もっともシンプルな場合で考えることにしたい。　


図１自動車のポンチ絵

図１の自動車のポンチ絵は自動車を横から見たイメージである（我ながら汚い絵だと思うが）。　路面はデコボコしているが、車体はガタガタしないイメージを描いたつもりである（分かりにくいのは勘弁願いたい）。

乗用車の場合、車体は前後二本、合計4本のバネで車体ととタイヤ（厳密には車軸）が連結されている。　では、そのバネをどうやって設計したらいいだろうか？　難しく考えれば限がないし、ブログで早々細かいこととは書けないので、大雑把に最も基本的な設計手法を書くことにする。　

前置きが長くなったが、下の図２にあるような、車体に相当する物体（質量ｍ）が、フックの法則が適用できるバネ（バネ定数はｋ）で地面とつながっていると考えることにする。


図２　車体の最もシンプルなモデル


実際には路面がデコボコしてるので、路面を変化させるべきなのだが、簡単に考えるために、車体の方が揺れるということにする。　これは、実際になされれるサスペンション設計の検討項目である。

ここまで長々とサスペンションの話をしてきたのだが、実は、図２のバネと箱（厳密には質点）の図を出したかったのである。　図２は高校の物理で単振動として習う図であるが、実際にこの単振動を自動車のサスペンション設計では使っている。　ちなみ、図２でaは箱（質点）の揺れを表す加速度で、ｘは箱の上下の位置を表す。aもxも大きさと向きをもつ。こういうのをベクトル量と言うが、今は二次方程式の話をしようとしているので、読み飛ばして頂きたい。

さて、この辺も読み飛ばして頂きたいのだが、箱（質点）の上下の位置ｘが時間ｔでどのように変化するかを計算で示そうとすると、運動方程式と言う微分方方程式を立てることになる。　上の場合であれば、以下のようになる。


mx''(t)+kx(t)=ma(t)

ここで、mx''(t)はxを時間tの2階微分である。　これは箱（質点ｍ）の実際に発生する加速度である。　a(t)は色んな場合があるので、一番簡単な場合を考える。　それはma(t)=0と考えることである。

そうなると、
mx''(t)+kx(t)=0
となる。

さぁ、問題はここからである。この式をどう解くか？ということだ。

誰が一番最初にしたのかは知らないのだが、先人達はこう言う解き方を見つけた。
x(t)=Csin(ωt)+Dcos(ωt)
としてみた。
そうすると、x(t)の一階微分（速度）は、





x(t)の二階微分（加速度）は





これを、
mx''(t)+kx(t)=0
に代入すると、





となって、ωの二次方程式が出てくる。　mx''(t)+kx(t)=-と言う微分方程式が、いつの間にかωの二次方程式になってしまったのである。

高校の物理の教科書で、単振動の共振周波数fはｆ＝２πω、ω＝√（k/m)と習うのであるが、この関係は上記のような関係からでてくる。

微分方程式は答えがあるとは限らないのだが、この単振動は厳密な答えが求まる稀な例である。そのため、理工系では頻繁に利用される。　その途中で二次方程式を使う。　

結局x(t)は、

となる。　CとDはｔ＝０のときに箱(質点ｍ）がどういう状態（これを初期条件と言う）で決まる。

これは、物理や機械のことを専門に大学で学んだ人ならば常識なのであるので、二次方程式は非常に身近な式である。　ところが、高校までは、二次方程式の解の公式、

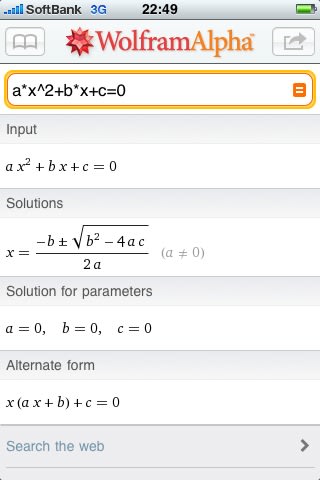
を覚えろとしか言われないので、√や虚数単位iが出てきたりして、何がなんだか分からない。　

ちなみに、これは、二次方程式の最も簡単な応用例である。　

ω＝√(k/m)もどういう性質を持つのかの説明も必要だろう。　これは、いずれするつもりである。

長々と書いて来たが、二次方程式の応用の結果を使って、自動車の基本設計がなされている。　自動車だけでなく、バネやゴムを使って振動を抑える機械は全てそうである。　これから先は専門的になるので、またの機会にする。　

この記事でひとつだけ理解して欲しいのは、機械を作るのに、二次方程式が使えることが必要であるということである。　それ以外は無視して頂いて構わない。

次回は、別の二次方程式の応用を書きたいと思う。　多分、行列とベクトルとの関係になると思う。

最後まで読んで頂いた方、ありがとうございました。

質問があれば、コメントでお願いします。