ここでユークリッド幾何学以外の基本的な2次元の幾何学について簡単に紹介しておきます。それは、ひとつは非ユークリッド幾何学と呼ばれるもので、曲率がゼロではない空間の幾何学です。もうひとつは、合同変換の成り立たない、アフィン幾何学、射影幾何学、位相幾何学(トポロジー)の系列です。実を言うとこのテーマに関する現在の日本語ウェブサイトの情報は貧困の一語に尽きますので、ここを見てくれ、で済ませることができません。しかし例えば後述のRef-3,5-7のような本がありますので参考にして下さい。
まず2次元空間すなわち曲面を考えると、曲率という指標で3種類に分類できます。それぞれの性質は次の表にまとめられます。
図をまとめた、こんなサイトもあります。
http://mathforum.org/mathimages/index.php/Hyperbolic_Geometry
楕円面(ellipsoid)とは楕円体(ellipsoid)の表面ですが、一般の楕円面では場所により曲率が異なります。曲面全体で曲率が等しい場合は球面になり、その幾何学は特に球面幾何学と呼ばれます。球面幾何学では直線に相当するのは、中心を通る平面と球面との交線である大円です。一般の曲面上の幾何学では2点間を結ぶ最短の線が直線に相当します(*1)。一般相対性理論ではこの最短線のことを測地線とも呼びます。
疑球面(pseudosphere)というのは耳慣れない人が多いと思いますが、全ての点で曲率が負の一定値となる曲面で、具体的にはトラクトリックス(tractrix)(牽引線とも訳されている)をその漸近線を軸として回転させた回転面です。残念なことに、ごらんの通り疑球面には鋭い端があり、無限に広がるはずの非ユートクリッド2次元空間の完全なモデルにはなっていません。実はRef-6(p101-2)によれば、「曲率がマイナスの定値をとって、しかも至るところ滑らかな曲面は三次元空間内に存在しない」ということがヒルベルトにより証明されています。
なお、曲率が正の曲面の幾何学は楕円幾何学(Elliptic geometry)、曲率が負の曲面の幾何学は双曲幾何学(hyperbolic geometry)と呼ばれ、双曲線の2次元版である双曲面(Hyperboloid)のうちの一葉双曲面も曲率が負で、その上では双曲幾何学が成り立ちます。しかしもちろん一葉双曲面の曲率は全ての点で同一ではありません。
さてヒルベルトの結合の公理1は「2点と結合する直線がつねにただひとつある」というものですが、球面では直径の両端を通る直線(大円)が無数にありますから、この公理は成立しません。しかし半球を考え、直線(大円)の両端を同一の点だと考えると、結合の公理1が成り立ち平行線の存在しない幾何学のモデルが出来上がります。この半球面を平面に投影して考えると図のようなモデルとなり、この平面を射影平面と呼びます(*2)。
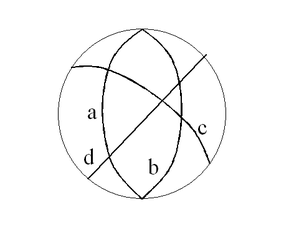
この図では一番外側の円周が境界を成しているように見えますが、直線上を進んでこの円周に達すると、そこの点は反対側の点と同一で、いわば反対の端にワープできるので、射影平面では直線上を進むと元の点に戻ってくるのです。よって、この円内の平面は境界のない有限な平面になります。なお、全球面を考え、直径の両端の点を同一の点と考えても等価なモデルが得られます。この方が全体が一様であることがわかりやすいかも知れません。
次に負の曲率の曲面の幾何学を平面上に表したモデル、すなわち平行線が無数にある平面のモデルとして、クライン平面とポワンカレ平面があります。それぞれ、クライン(Felix C. Klein)およびアンリ・ポワンカレ(Jules-Henri Poincaré)により作られたモデルです。
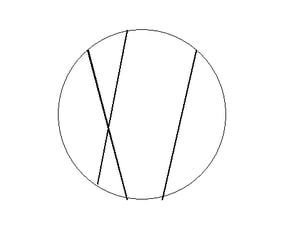
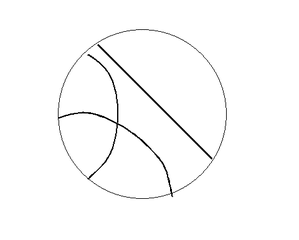
どちらのモデルも円内の距離の定義が通常とは異なっていて、一番外側の円周に近づくほど見かけの距離が小さくなるように定義され、一番外側の円周は無限遠になっています。つまり、円内で交わっていない2つの直線はモデル平面では交点を持たないということになり、平行線となります。両者とも本質的には同じモデルで、違いは直線に相当するものが見かけ上、クライン平面では弦であり、ポワンカレ平面では円弧の場合もあるという点です。Ref-6の第3部と補講3では、半球面上に作った非ユークリッドモデルからクライン平面を具体的に誘導しています。Ref-7では直接的にクライン・モデルとして構成し説明しています。
なお、Ref-3には多くの幾何学モデルが登場しますが、ポワンカレ平面はモデル9(例1.9)としてポワンカレ結合平面という名で、クライン平面はモデル10(例1.10)としてケイレイ=クライン結合平面という名で登場します。それぞれ英語では、"Poincaré disk model"および"Klein-Beltrami model"と呼ばれることが多いようです。
http://www.britannica.com/EBchecked/topic-art/417456/67391/In-the-Klein-Beltrami-model-for-the-hyperbolic-plane-the ブリタニカ
http://www.geom.uiuc.edu/~crobles/hyperbolic/hypr/modl/
ケイレイとは19世紀イギリスの数学者アーサー・ケイリー(Arthur Cayley)のことで、Ref-6(p146)によれば「友人からちょうど噂にのぼり始めたばかりの非ユークリッド幾何の話をきかされた」途端に「前にサーモン(一八一九~一九一四)の円錐曲線論で読んだ覚えのあるケーリー(一八二一~一八九五)の射影的計量というものとどうも関係がありそうだ、と直感した」のだそうです。
参考図書(1-4は01/01記事と同じ)
1) 中村幸四郎、他 『ユークリッド原論』共立出版; 縮刷版(1996/6/1),ISBN-10: 4320015134
2) エウクレイデス(著),斎藤憲(訳),三浦伸夫(訳)『エウクレイデス全集-第1巻(1)』東京大学出版会(2008/01), ISBN-10: 4130653016
3) 溝上武実 『初等幾何入門―公理から考える』日本評論社(2005/09), ISBN-10: 4535784396
4) D.ヒルベルト(David Hilbert),中村幸四郎(訳)『幾何学基礎論 (ちくま学芸文庫)』筑摩書房 (2005/12) ISBN-10: 4480089535
5) 西山享(Kyo Nishiyama)『よくわかる幾何学―複素平面・初等幾何学・射影幾何学をめぐって』丸善 (2004/02) ISBN-10: 4621073702
6) 寺阪英孝『非ユークリッド幾何の世界―幾何学の原点をさぐる(ブルーバックス312)』講談社 (1977/01) ISBN-10: 4061179128
7) 瀬山士郎『幾何物語―現代幾何学の不思議な世界 (ちくま学芸文庫)』筑摩書房(2007/12) ISBN-10: 4480091262
*1) 最短の線を定義するには距離が定義されていなくてはならないが、直線の定義そのものは距離を使わない方法が普通のようだ。
*2) 射影平面というと次回に述べる射影幾何学が成立する平面という意味が強く、そこでは距離が定義されていないのだが、ここでの射影平面は距離が定義された2次元空間であり、位相構造が第一義の射影平面と同じものだと言える。
まず2次元空間すなわち曲面を考えると、曲率という指標で3種類に分類できます。それぞれの性質は次の表にまとめられます。
| 曲率 | 例 | 平行線数 | 三角形の内角の和 |
| 正 | 楕円面 | 0 | 180度より大 |
| ゼロ | 平面 | 1 | 180度 |
| 負 | 疑球面 | 無数 | 180度より小 |
図をまとめた、こんなサイトもあります。
http://mathforum.org/mathimages/index.php/Hyperbolic_Geometry
楕円面(ellipsoid)とは楕円体(ellipsoid)の表面ですが、一般の楕円面では場所により曲率が異なります。曲面全体で曲率が等しい場合は球面になり、その幾何学は特に球面幾何学と呼ばれます。球面幾何学では直線に相当するのは、中心を通る平面と球面との交線である大円です。一般の曲面上の幾何学では2点間を結ぶ最短の線が直線に相当します(*1)。一般相対性理論ではこの最短線のことを測地線とも呼びます。
疑球面(pseudosphere)というのは耳慣れない人が多いと思いますが、全ての点で曲率が負の一定値となる曲面で、具体的にはトラクトリックス(tractrix)(牽引線とも訳されている)をその漸近線を軸として回転させた回転面です。残念なことに、ごらんの通り疑球面には鋭い端があり、無限に広がるはずの非ユートクリッド2次元空間の完全なモデルにはなっていません。実はRef-6(p101-2)によれば、「曲率がマイナスの定値をとって、しかも至るところ滑らかな曲面は三次元空間内に存在しない」ということがヒルベルトにより証明されています。
なお、曲率が正の曲面の幾何学は楕円幾何学(Elliptic geometry)、曲率が負の曲面の幾何学は双曲幾何学(hyperbolic geometry)と呼ばれ、双曲線の2次元版である双曲面(Hyperboloid)のうちの一葉双曲面も曲率が負で、その上では双曲幾何学が成り立ちます。しかしもちろん一葉双曲面の曲率は全ての点で同一ではありません。
さてヒルベルトの結合の公理1は「2点と結合する直線がつねにただひとつある」というものですが、球面では直径の両端を通る直線(大円)が無数にありますから、この公理は成立しません。しかし半球を考え、直線(大円)の両端を同一の点だと考えると、結合の公理1が成り立ち平行線の存在しない幾何学のモデルが出来上がります。この半球面を平面に投影して考えると図のようなモデルとなり、この平面を射影平面と呼びます(*2)。

この図では一番外側の円周が境界を成しているように見えますが、直線上を進んでこの円周に達すると、そこの点は反対側の点と同一で、いわば反対の端にワープできるので、射影平面では直線上を進むと元の点に戻ってくるのです。よって、この円内の平面は境界のない有限な平面になります。なお、全球面を考え、直径の両端の点を同一の点と考えても等価なモデルが得られます。この方が全体が一様であることがわかりやすいかも知れません。
次に負の曲率の曲面の幾何学を平面上に表したモデル、すなわち平行線が無数にある平面のモデルとして、クライン平面とポワンカレ平面があります。それぞれ、クライン(Felix C. Klein)およびアンリ・ポワンカレ(Jules-Henri Poincaré)により作られたモデルです。


どちらのモデルも円内の距離の定義が通常とは異なっていて、一番外側の円周に近づくほど見かけの距離が小さくなるように定義され、一番外側の円周は無限遠になっています。つまり、円内で交わっていない2つの直線はモデル平面では交点を持たないということになり、平行線となります。両者とも本質的には同じモデルで、違いは直線に相当するものが見かけ上、クライン平面では弦であり、ポワンカレ平面では円弧の場合もあるという点です。Ref-6の第3部と補講3では、半球面上に作った非ユークリッドモデルからクライン平面を具体的に誘導しています。Ref-7では直接的にクライン・モデルとして構成し説明しています。
なお、Ref-3には多くの幾何学モデルが登場しますが、ポワンカレ平面はモデル9(例1.9)としてポワンカレ結合平面という名で、クライン平面はモデル10(例1.10)としてケイレイ=クライン結合平面という名で登場します。それぞれ英語では、"Poincaré disk model"および"Klein-Beltrami model"と呼ばれることが多いようです。
http://www.britannica.com/EBchecked/topic-art/417456/67391/In-the-Klein-Beltrami-model-for-the-hyperbolic-plane-the ブリタニカ
http://www.geom.uiuc.edu/~crobles/hyperbolic/hypr/modl/
ケイレイとは19世紀イギリスの数学者アーサー・ケイリー(Arthur Cayley)のことで、Ref-6(p146)によれば「友人からちょうど噂にのぼり始めたばかりの非ユークリッド幾何の話をきかされた」途端に「前にサーモン(一八一九~一九一四)の円錐曲線論で読んだ覚えのあるケーリー(一八二一~一八九五)の射影的計量というものとどうも関係がありそうだ、と直感した」のだそうです。
参考図書(1-4は01/01記事と同じ)
1) 中村幸四郎、他 『ユークリッド原論』共立出版; 縮刷版(1996/6/1),ISBN-10: 4320015134
2) エウクレイデス(著),斎藤憲(訳),三浦伸夫(訳)『エウクレイデス全集-第1巻(1)』東京大学出版会(2008/01), ISBN-10: 4130653016
3) 溝上武実 『初等幾何入門―公理から考える』日本評論社(2005/09), ISBN-10: 4535784396
4) D.ヒルベルト(David Hilbert),中村幸四郎(訳)『幾何学基礎論 (ちくま学芸文庫)』筑摩書房 (2005/12) ISBN-10: 4480089535
5) 西山享(Kyo Nishiyama)『よくわかる幾何学―複素平面・初等幾何学・射影幾何学をめぐって』丸善 (2004/02) ISBN-10: 4621073702
6) 寺阪英孝『非ユークリッド幾何の世界―幾何学の原点をさぐる(ブルーバックス312)』講談社 (1977/01) ISBN-10: 4061179128
7) 瀬山士郎『幾何物語―現代幾何学の不思議な世界 (ちくま学芸文庫)』筑摩書房(2007/12) ISBN-10: 4480091262
*1) 最短の線を定義するには距離が定義されていなくてはならないが、直線の定義そのものは距離を使わない方法が普通のようだ。
*2) 射影平面というと次回に述べる射影幾何学が成立する平面という意味が強く、そこでは距離が定義されていないのだが、ここでの射影平面は距離が定義された2次元空間であり、位相構造が第一義の射影平面と同じものだと言える。

























