ベルトランの箱の逆説に刺激されて3囚人問題やモンティ・ホール問題が生まれたとの話もあり、この3つは関係が深い(数学的構造が似ている)との認識が一般的なようなので、前回述べた「ベルトランの箱は病気検査問題と同じ」という見解は少し異端と言えるかも知れません。なので少ししつこく説明しておきます。
【モンティ問題とベルトランの箱との違い】
3つの箱を使うという共通点のあるモンティ・ホール問題とベルトランの箱のパラドックスを比較して見ます。
モンティ・ホール問題
第1ステップ) 箱をひとつ選択、事前確率を想定
選んだ箱が当たり(賞品入り)である確率、1/3
第2ステップ) 新たな情報を得る
残りの箱の1つが外れと判明
第3ステップ) 事後確率を求める
選んだ箱が当たりである確率
ベルトランの箱
第1ステップ) 箱をひとつ選択、事前確率を想定
選んだ箱が当たり(金金)である確率、1/3
第2ステップ) 新たな情報を得る
選んだ箱に金が1つあることが判明
第3ステップ) 事後確率を求める
選んだ箱が当たりである確率
このように両者の違いは第2ステップで得られる新しい情報の種類です。モンティでは選ばなかった箱についての情報が得られますが、ベルトランでは選んだ箱についての情報が得られます。病気検査で選ばれた人(検査を受けた人)の検査結果がわかるのと同じなのです。これが違うのですから、両者には大きな違いが出てきます。例えば問題を拡張しようとしてみると、よりはっきりと違いが出てきます。
モンティ・ホールで箱の数を増やすと事前確率も事後確率も変化します。
ベルトランの箱では、銀銀の箱の数を変えると事前確率は変化しますが事後確率は変化しません。事後には選んだ箱が銀銀ではないことが判明するからです。これが「引き出しから銀が出た」という設定だと金金の箱の数が無関係になります。
ベルトランの箱は病気検査の問題と対応しており、金金の箱と金銀の箱との比率(感染率に対応)や、各箱の中の金と銀との比率(検査に対する陽性率)が変化すると事後確率が変化します。次のようなモデルは、実は一般的な病気検査とよりよく対応しているのかも知れません。
各箱は千個の引き出しを持ちそれぞれに金または銀が入っている。
(金または空とした方が陽性と陰性のイメージに近いかも)
金入り引き出しを500個以上持つ箱を当たり、500個未満の箱を外れとする。
当たりの箱の引き出し全部のうち、金入り引き出しの比率はわかっている(1-偽陰性率)。
外れの箱の引き出し全部のうち、金入り引き出しの比率はわかっている(偽陽性率)。
3囚人問題とモンティ・ホール問題は箱を人に変えれば上記の3ステップは全く同じです。2つの問題の違いは前者では選んだ箱(自分)を他の箱と交換できないことだけです。
病気検査のベルトランの箱との違いは、箱の数が非常に多く、引き出しの数は実質的に実数である、という点であり、これは他の2つの問題との違いでもあります。モンティ・ホールや3囚人問題で同様な拡張をすると何か実際に当てはめられるでしょうか? 実際の問題があるかどうかはともかく、次のように一般化することはできるでしょう。
【拡張問題】
非常に多くの箱があり、それらが2つのグループGとHに分けられている。箱の中のいくつかに当たり賞品が入っている。
nG:グループGの箱の数 nH:グループHの箱の数 nA:全体の箱の数
nA=nG+nH
mG:グループGの当たりの数 mH:グループHの当たりの数 mA:全体の当たりの数
mA=mG+mH
pG:グループGの当たり頻度 pH:グループHの当たり頻度 pA:全体の当たり頻度
pG=mG/nG pH=mH/nH pA=mA/nA
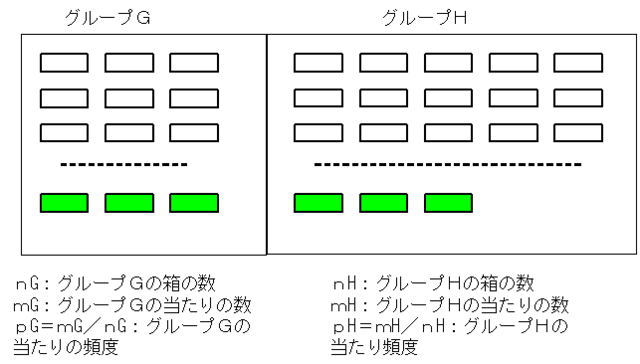
事前にわかっていることは、各箱がどのグループに属しているか、各グループの箱の数(nGとnH)、全体の当たり頻度pA、である。
ゆえに、nA=nG+nH、mA=nA✕pA、もわかっている。
問いは、グループGの当たりの数mG、つまりは当たり頻度pG=mG/nGの値である。
当然、mH=mA-mG、pH=mH/nH、を求めてもよい。
なお各箱が、GおよびHとラベル付けした中の見えない2つの大きな容器に入れてあるという状況なら、手に取った箱がどのグループに属していたかはわかるが、nGとnHはわからない。
第1ステップ) pG=pH=pA、とみなす。つまりグループGとグループHに分布の偏りはないとみなす。事前確率を想定したことになる。
第2ステップ) グループHの箱をsH個開くとtH個が当たりだった。
第3ステップ) pGを推定する。事後確率を求めることになる。

第2ステップで当たりの箱も開く点はモンティ問題や3囚人問題と違って見えるかも知れません。特に、「司会者や看守が当たりの箱を知っていて必ず外れを選ぶ」「司会者や看守が当たりの箱を知っていることを、回答者が知っている」という点も問題のポイントだとの見解もあります。しかし上記のように一般化すれば、もし司会者や看守が箱の中身を知らずにsH個の箱をランダムに選ぶ場合は、単にtH個の数値が異なる問題になるだけです。当然、解答も異なるでしょう。
モンティ問題では、nH=2、sH=1、tH=0ですが、司会者が開いた箱が当たりだった場合(tH=1)は確実にpG=0でmG=0と求められます。つまり、もし司会者が箱の中身を知らずに選ぶなら、1/3の確率でつまらない問題になってショーとしてはおもしろくなくなるだけのことです。3囚人問題では看守が死刑になる者を知らないことは非常に考えにくいですから、モンティ問題に比べるとこの点でも自然に制限が加わっていることになります。
-------追記(2020/05/31) 以上2節は私の間違い。-------
1/3の確率で開けた箱が当たりでつまらなくなり、1/3の確率で開けた箱が外れで且つ選んだ箱が当たり、1/3の確率で開けた箱が外れで且つ選ばなかったもう一つの箱が当たり、となる。ゆえに、交換してもしてなくても当たりの確率は同じ。[*1]でもう少し詳しく。
-------追記終わり-----------------------
ただし箱の数が増えた場合は、ランダムに選んだのか否かを知っているかどうかで、tHとsHの値からグループのまだ閉じている箱のうちで当たりの箱の数を推定する方法に違いが出てきます。それどころか、tHとsHの値から本当にランダムに選んでいた確率を求めることもできそうです。ややこしくなりますね。
以上の考察では確率ではなく頻度を求めることにしてしまいましたが、これは箱の数が多いと、1つの箱を選んだときの当たりの確率が当たりの箱の頻度に等しくなるからです。もしくは等しくなると仮定するのが自然だからです。この辺りの機微は本ブログ「確率を観測する」で少し書きました。これって頻度主義でしょうか?
さてここでグループHがグループH1とグループH2に分かれていて、H1とH2のうちどちらかを選んでそのグループの箱を全て開く、という想定だと、元のモンティ問題に近づくように見えます。でもこれは、開いた箱のグループを例えばH2と名付けたというだけになるでしょう。正確に言うと、一度にsH個の箱を選んで例えばグループH2と名付けて、それらを一斉に開いた場合と同じことになります。1個ずつ開いた場合は開くたびに当たり箱の数という結果が出るので、得られる情報量が増えることになるでしょう、たぶん。

さらに、上記のGやHのグループを瓶などの容器にし、中身の箱を液体にすれば頻度が有理数(整数/整数)ではなく実数になります。この設定だと、例えば瓶をGの他にH1とH2を用意して、H1とH2のどちらかの液量を知らせるという形になるでしょう。液体にすると中身は均一という条件が自動的に入るので大きな違いが出てきますが。

色々な拡張や変形があり奥が深そうですが、これくらいにしましょう。
さてこれらの問題は、事前確率から事後確率を得るという解き方をしないといけないのでベイズ主義の解法になるのでしょうか? でもそれは問題の設定であって、頻度主義だからと文句を言えるものではないでしょう。次回はベイズ主義と頻度主義の違いについて、どんな見解があるのかを調べてみます。
----------------------
*1) 追記(2020/05/31) 同じ数の当たりの箱と外れの箱とで開かれる確率が異なると、事後確率も異なってくるということ。モンティ・ホールでは当たりの箱が開く確率は1でハズレの箱は0、ランダムに開くなら両方とも0.5。開かれる確率が異なる原因はモンティ・ホールでは開く者の意思だが、何らかの自然的原因や自動的原因だとしても数学的には同じである。さらに、この確率の偏りについて知っているかどうかで、予測できる事後確率は異なってくる。
選ばなかった箱の数が多く、少しずつ開いていくごとに当たりの数のデータを取ると、開き方がランダムかどうかも推測ができるようになるのは、元の文でも少し示唆した通り。ただしこれは、当たりの比率がある程度の大きさがないと、ほとんどは外れという結果になりデータが取れない。
----------------------
Ref-1) ベイズ統計概説
Ref-1a) ニュートン別冊「ゼロからわかる統計と確率 ベイズ統計編」
Ref-1b) 松原望「ベイジアンの源流--トーマス・ベイズをめぐって」オベレーションズ・リサーチ(1983/09) p432-438
Ref-2) ベイズ論 vs 頻度論
Ref-2a) Diamond Online『「頻度論」の学者と「ベイズ論」の学者が対談したら』(2015/03/03)
Ref-2b) hidekatsu-izuno 日々の記録「ベイズ統計学に関する議論を整理する」(2020/12/12)
Ref-2c) 。「統計学はなぜ哲学の問題になるのか」 大塚 (2021),『哲學研究』606:1-24. プレプリント版。大塚淳『統計学を哲学する』名古屋大学出版会(2020/10/26) ISBN-13:978-4815810030、リンク先に詳しい目次あり。
Ref-2d) ダレル・P.ロウボトム;佐竹佑介(訳)『現代哲学のキーコンセプト 確率』岩波書店(2019/06/19) ISBN=9-784-00061346-0、リンク先に詳しい目次あり
Ref-2e) 赤池弘次「統計的推論のパラダイムの変遷について」統計数理研究所集報(1980) Vol.27,No.1,p5-12
Ref-3) Avilen「ベイズ統計の記事一覧」。初心者向け解説のベイズ統計学の解説。
Ref-3a) ベイズ統計学とは?初心者向けのやさしい解説
Ref-3b) ベイズ統計学の考え方〜ベイズ論と頻度論の違い〜
Ref-3c) ベイズ推定と最尤推定の違いを例題を用いて解説
Ref-3d) ベイズ推定量の導出!例題と解説(最尤推定量と比較)
Ref-4) 渡辺澄夫(東京工業大学)『ベイズ統計の理論と方法』コロナ社(2012/04/12) ISBN=978-4-339-02462-3、リンク先に詳しい目次あり。最新の良さそうな教科書。
Ref-4a) 著者自身による解説
Ref-4b) 統計学入門「主義」を心配するみなさまに。数理科学に主義なんて不要だよ、という解説。
Ref-5) モンティ・ホール問題・三囚人問題・ベルトランの箱
Ref-5a) モンティ・ホール問題好きのホームページより「Web上のわかりやすい説明」。深すぎて迷いそうです。
Ref-5b) 生きてる感想「モンティ・ホール問題・三囚人問題・ベルトランの箱のパラドクス」(2016/02/16)。必要なことが一番まとまってると、私は思う。
Ref-5c) 菊池耕士「モンティ・ホール問題における最尤法」 目白大学 総合科学研究 06号 (2010/03) p149-158。頻度主義でも解けるよ、という見解のひとつを表明。
【モンティ問題とベルトランの箱との違い】
3つの箱を使うという共通点のあるモンティ・ホール問題とベルトランの箱のパラドックスを比較して見ます。
モンティ・ホール問題
第1ステップ) 箱をひとつ選択、事前確率を想定
選んだ箱が当たり(賞品入り)である確率、1/3
第2ステップ) 新たな情報を得る
残りの箱の1つが外れと判明
第3ステップ) 事後確率を求める
選んだ箱が当たりである確率
ベルトランの箱
第1ステップ) 箱をひとつ選択、事前確率を想定
選んだ箱が当たり(金金)である確率、1/3
第2ステップ) 新たな情報を得る
選んだ箱に金が1つあることが判明
第3ステップ) 事後確率を求める
選んだ箱が当たりである確率
このように両者の違いは第2ステップで得られる新しい情報の種類です。モンティでは選ばなかった箱についての情報が得られますが、ベルトランでは選んだ箱についての情報が得られます。病気検査で選ばれた人(検査を受けた人)の検査結果がわかるのと同じなのです。これが違うのですから、両者には大きな違いが出てきます。例えば問題を拡張しようとしてみると、よりはっきりと違いが出てきます。
モンティ・ホールで箱の数を増やすと事前確率も事後確率も変化します。
ベルトランの箱では、銀銀の箱の数を変えると事前確率は変化しますが事後確率は変化しません。事後には選んだ箱が銀銀ではないことが判明するからです。これが「引き出しから銀が出た」という設定だと金金の箱の数が無関係になります。
ベルトランの箱は病気検査の問題と対応しており、金金の箱と金銀の箱との比率(感染率に対応)や、各箱の中の金と銀との比率(検査に対する陽性率)が変化すると事後確率が変化します。次のようなモデルは、実は一般的な病気検査とよりよく対応しているのかも知れません。
各箱は千個の引き出しを持ちそれぞれに金または銀が入っている。
(金または空とした方が陽性と陰性のイメージに近いかも)
金入り引き出しを500個以上持つ箱を当たり、500個未満の箱を外れとする。
当たりの箱の引き出し全部のうち、金入り引き出しの比率はわかっている(1-偽陰性率)。
外れの箱の引き出し全部のうち、金入り引き出しの比率はわかっている(偽陽性率)。
3囚人問題とモンティ・ホール問題は箱を人に変えれば上記の3ステップは全く同じです。2つの問題の違いは前者では選んだ箱(自分)を他の箱と交換できないことだけです。
病気検査のベルトランの箱との違いは、箱の数が非常に多く、引き出しの数は実質的に実数である、という点であり、これは他の2つの問題との違いでもあります。モンティ・ホールや3囚人問題で同様な拡張をすると何か実際に当てはめられるでしょうか? 実際の問題があるかどうかはともかく、次のように一般化することはできるでしょう。
【拡張問題】
非常に多くの箱があり、それらが2つのグループGとHに分けられている。箱の中のいくつかに当たり賞品が入っている。
nG:グループGの箱の数 nH:グループHの箱の数 nA:全体の箱の数
nA=nG+nH
mG:グループGの当たりの数 mH:グループHの当たりの数 mA:全体の当たりの数
mA=mG+mH
pG:グループGの当たり頻度 pH:グループHの当たり頻度 pA:全体の当たり頻度
pG=mG/nG pH=mH/nH pA=mA/nA

事前にわかっていることは、各箱がどのグループに属しているか、各グループの箱の数(nGとnH)、全体の当たり頻度pA、である。
ゆえに、nA=nG+nH、mA=nA✕pA、もわかっている。
問いは、グループGの当たりの数mG、つまりは当たり頻度pG=mG/nGの値である。
当然、mH=mA-mG、pH=mH/nH、を求めてもよい。
なお各箱が、GおよびHとラベル付けした中の見えない2つの大きな容器に入れてあるという状況なら、手に取った箱がどのグループに属していたかはわかるが、nGとnHはわからない。
第1ステップ) pG=pH=pA、とみなす。つまりグループGとグループHに分布の偏りはないとみなす。事前確率を想定したことになる。
第2ステップ) グループHの箱をsH個開くとtH個が当たりだった。
第3ステップ) pGを推定する。事後確率を求めることになる。

第2ステップで当たりの箱も開く点はモンティ問題や3囚人問題と違って見えるかも知れません。特に、「司会者や看守が当たりの箱を知っていて必ず外れを選ぶ」「司会者や看守が当たりの箱を知っていることを、回答者が知っている」という点も問題のポイントだとの見解もあります。しかし上記のように一般化すれば、もし司会者や看守が箱の中身を知らずにsH個の箱をランダムに選ぶ場合は、単にtH個の数値が異なる問題になるだけです。当然、解答も異なるでしょう。
モンティ問題では、nH=2、sH=1、tH=0ですが、司会者が開いた箱が当たりだった場合(tH=1)は確実にpG=0でmG=0と求められます。つまり、もし司会者が箱の中身を知らずに選ぶなら、1/3の確率でつまらない問題になってショーとしてはおもしろくなくなるだけのことです。3囚人問題では看守が死刑になる者を知らないことは非常に考えにくいですから、モンティ問題に比べるとこの点でも自然に制限が加わっていることになります。
-------追記(2020/05/31) 以上2節は私の間違い。-------
1/3の確率で開けた箱が当たりでつまらなくなり、1/3の確率で開けた箱が外れで且つ選んだ箱が当たり、1/3の確率で開けた箱が外れで且つ選ばなかったもう一つの箱が当たり、となる。ゆえに、交換してもしてなくても当たりの確率は同じ。[*1]でもう少し詳しく。
-------追記終わり-----------------------
ただし箱の数が増えた場合は、ランダムに選んだのか否かを知っているかどうかで、tHとsHの値からグループのまだ閉じている箱のうちで当たりの箱の数を推定する方法に違いが出てきます。それどころか、tHとsHの値から本当にランダムに選んでいた確率を求めることもできそうです。ややこしくなりますね。
以上の考察では確率ではなく頻度を求めることにしてしまいましたが、これは箱の数が多いと、1つの箱を選んだときの当たりの確率が当たりの箱の頻度に等しくなるからです。もしくは等しくなると仮定するのが自然だからです。この辺りの機微は本ブログ「確率を観測する」で少し書きました。これって頻度主義でしょうか?
さてここでグループHがグループH1とグループH2に分かれていて、H1とH2のうちどちらかを選んでそのグループの箱を全て開く、という想定だと、元のモンティ問題に近づくように見えます。でもこれは、開いた箱のグループを例えばH2と名付けたというだけになるでしょう。正確に言うと、一度にsH個の箱を選んで例えばグループH2と名付けて、それらを一斉に開いた場合と同じことになります。1個ずつ開いた場合は開くたびに当たり箱の数という結果が出るので、得られる情報量が増えることになるでしょう、たぶん。

さらに、上記のGやHのグループを瓶などの容器にし、中身の箱を液体にすれば頻度が有理数(整数/整数)ではなく実数になります。この設定だと、例えば瓶をGの他にH1とH2を用意して、H1とH2のどちらかの液量を知らせるという形になるでしょう。液体にすると中身は均一という条件が自動的に入るので大きな違いが出てきますが。

色々な拡張や変形があり奥が深そうですが、これくらいにしましょう。
さてこれらの問題は、事前確率から事後確率を得るという解き方をしないといけないのでベイズ主義の解法になるのでしょうか? でもそれは問題の設定であって、頻度主義だからと文句を言えるものではないでしょう。次回はベイズ主義と頻度主義の違いについて、どんな見解があるのかを調べてみます。
----------------------
*1) 追記(2020/05/31) 同じ数の当たりの箱と外れの箱とで開かれる確率が異なると、事後確率も異なってくるということ。モンティ・ホールでは当たりの箱が開く確率は1でハズレの箱は0、ランダムに開くなら両方とも0.5。開かれる確率が異なる原因はモンティ・ホールでは開く者の意思だが、何らかの自然的原因や自動的原因だとしても数学的には同じである。さらに、この確率の偏りについて知っているかどうかで、予測できる事後確率は異なってくる。
選ばなかった箱の数が多く、少しずつ開いていくごとに当たりの数のデータを取ると、開き方がランダムかどうかも推測ができるようになるのは、元の文でも少し示唆した通り。ただしこれは、当たりの比率がある程度の大きさがないと、ほとんどは外れという結果になりデータが取れない。
----------------------
Ref-1) ベイズ統計概説
Ref-1a) ニュートン別冊「ゼロからわかる統計と確率 ベイズ統計編」
Ref-1b) 松原望「ベイジアンの源流--トーマス・ベイズをめぐって」オベレーションズ・リサーチ(1983/09) p432-438
Ref-2) ベイズ論 vs 頻度論
Ref-2a) Diamond Online『「頻度論」の学者と「ベイズ論」の学者が対談したら』(2015/03/03)
Ref-2b) hidekatsu-izuno 日々の記録「ベイズ統計学に関する議論を整理する」(2020/12/12)
Ref-2c) 。「統計学はなぜ哲学の問題になるのか」 大塚 (2021),『哲學研究』606:1-24. プレプリント版。大塚淳『統計学を哲学する』名古屋大学出版会(2020/10/26) ISBN-13:978-4815810030、リンク先に詳しい目次あり。
Ref-2d) ダレル・P.ロウボトム;佐竹佑介(訳)『現代哲学のキーコンセプト 確率』岩波書店(2019/06/19) ISBN=9-784-00061346-0、リンク先に詳しい目次あり
Ref-2e) 赤池弘次「統計的推論のパラダイムの変遷について」統計数理研究所集報(1980) Vol.27,No.1,p5-12
Ref-3) Avilen「ベイズ統計の記事一覧」。初心者向け解説のベイズ統計学の解説。
Ref-3a) ベイズ統計学とは?初心者向けのやさしい解説
Ref-3b) ベイズ統計学の考え方〜ベイズ論と頻度論の違い〜
Ref-3c) ベイズ推定と最尤推定の違いを例題を用いて解説
Ref-3d) ベイズ推定量の導出!例題と解説(最尤推定量と比較)
Ref-4) 渡辺澄夫(東京工業大学)『ベイズ統計の理論と方法』コロナ社(2012/04/12) ISBN=978-4-339-02462-3、リンク先に詳しい目次あり。最新の良さそうな教科書。
Ref-4a) 著者自身による解説
Ref-4b) 統計学入門「主義」を心配するみなさまに。数理科学に主義なんて不要だよ、という解説。
Ref-5) モンティ・ホール問題・三囚人問題・ベルトランの箱
Ref-5a) モンティ・ホール問題好きのホームページより「Web上のわかりやすい説明」。深すぎて迷いそうです。
Ref-5b) 生きてる感想「モンティ・ホール問題・三囚人問題・ベルトランの箱のパラドクス」(2016/02/16)。必要なことが一番まとまってると、私は思う。
Ref-5c) 菊池耕士「モンティ・ホール問題における最尤法」 目白大学 総合科学研究 06号 (2010/03) p149-158。頻度主義でも解けるよ、という見解のひとつを表明。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます