こんにちは。東久留米市の学習塾塾長です。
教室の掃除をすると汗ばむほど暖かく良い天気になりました。ところが天気図を見ると、西から前線を伴う低気圧が近づいていて、明日からしばらくぱっとしない天気が続くようです。
さて、今回は平成22年度京大入試問題(前期、理系)です。
問題は、
「xを正の実数とする。座標平面上の3点A(0,1)、B(0,2)、P(x,x)をとり、△APBを考える。xの値が変化するとき、∠APBの最大値を求めよ。」
です。
三角関数の余弦定理を使えば簡単に解けそうですが(実際にやってみると結構煩雑です。後半で紹介します)、これは高校で勉強するので、図形を利用して解いてみましょう。
まず図1のように、問題を図に表します。

▲図1.問題を図に表しました
問題は、点Pがy=x(x>0)上を動くとき、θの最大値はいくつかということです。
そこで図2のように、線分ABを弦とし、その円周がy=xと交点を持つ円を描き、交点の一つをPとします。

▲図2.線分ABを弦とする円を描きました
このとき、直線y=xの点A、Bと反対側の円周上に点Qをとることができ、∠APBと∠AQBは弧ABに対しての円周角なので、∠APB=∠AQBです。
次に、点Aと点Qを結んだ直線と直線y=xとの交点をP’とすると、∠AP’B>∠AQB(∠AP’B=∠AQB+∠P’BQ)で、∠AP’B>∠APBになります。
つまり、線分ABを弦とする円の弧が、直線y=xの点A、Bと反対側にあるとき、∠AQB=∠APBとなる点Qをとることができ、そのとき、∠AP’B>∠APBなので、∠APBは最大ではありません。∠APBが最大になるのは、点Qを取れないときで、それは円が直線y=xに接するときになり、このとき接点がPになります。
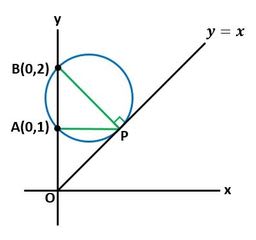
▲図3.線分ABを弦とする円と直線y=xの接点がPのとき、∠APBは最大になります
このとき、直線BPは、傾き-1、切片2の直線で、それはy=-x+2です。これとy=xの交点Pは、(1,1)になります。
したがって、△ABPは、∠BAP=90°の直角二等辺三角形になり、∠APBの最大値は45°=π/4で、これが答えです。
続いて、三角関数を利用して解いてみましょう。
図4の△ABPで、∠APB=θとします。

▲図4.三角関数を利用します
まず初めに、θの範囲を調べましょう。
点Pが直線y=x上を原点に近づいていくと、θは0に近づきます。
また、図5のように線分ABを直径とする円を考えたとき、この円周上の点をQとすると、∠AQB=90°で、さらに、この円周と直線y=xは交点を持たないので、θ<∠AQB=90°です。

▲図5.θ<90°です
以上から、0<θ<90°になります。
次に余弦定理を使って、cosθを表すと、
cosθ=(PA^2+PB^2-AB^2)/(2PA・PB)
です。
これに
PA=√(x^2+(x-1)^2)
PB=√(x^2+(x-2)^2)
AB=1
を代入すると、
cosθ=((x^2+(x-1)^2)+(x^2+(x-2)^2)-1)/2√((x^2+(x-1)^2)(x^2+(x-2)^2)
=(2x^2-3x+2)/√((2x^2-2x+1)(2x^2-4x+4))
=√((4x^4-12x^3+17x^2-12x+4)/(4x^4-12x^3+18x^2-12x+4))
です。
これを見ると大変複雑な式になってしまいましたが、t=x+1/xとすると、x^2+1/x^2=t^2-2なので、
cosθ=√((4t^2-12t+9)/(4t^2-12t+10))
=√(1-1/(4t^2-12t+10))
と簡単な式にすることができます。
ここでちょっと、θとcosθの関係を調べておくと、0<θ<90°でcosθは単調に減少するので、θが最大になるとき、cosθは最小になります。これは、1-1/(4t^2-12t+10)が最小になるとき、つまり、4t^2-12t+10が最小になるとき、θは最大値となるということです。
次に、tの取り得る範囲を調べておくと、t=x+1/xなので、相加相乗平均の関係から、t=x+1/x≧2√(x・1/x)=2(等号はx=1のとき成り立ちます)です。
以上から、t≧2の範囲で、4t^2-12t+10が最小になるとき、θは最大値となるということです。
そこで、
4t^2-12t+10=4(t^2-3)+10
=4((t-3/2)^2-9/4)+10
=4(t-3/2)^2+1
と変形すると、t≧2の範囲で4t^2-12t+10が最小になるのは、t=2のときです。
このとき、
cosθ=√(1-1/(16-24+10))
=√(1-1/2)
=1/√2
なので、θ=45°=π/4で、図形から導いた答えと一致しました。
三角関数は高校で勉強しますが、興味のある人は調べてみてください。
教室の掃除をすると汗ばむほど暖かく良い天気になりました。ところが天気図を見ると、西から前線を伴う低気圧が近づいていて、明日からしばらくぱっとしない天気が続くようです。
さて、今回は平成22年度京大入試問題(前期、理系)です。
問題は、
「xを正の実数とする。座標平面上の3点A(0,1)、B(0,2)、P(x,x)をとり、△APBを考える。xの値が変化するとき、∠APBの最大値を求めよ。」
です。
三角関数の余弦定理を使えば簡単に解けそうですが(実際にやってみると結構煩雑です。後半で紹介します)、これは高校で勉強するので、図形を利用して解いてみましょう。
まず図1のように、問題を図に表します。

▲図1.問題を図に表しました
問題は、点Pがy=x(x>0)上を動くとき、θの最大値はいくつかということです。
そこで図2のように、線分ABを弦とし、その円周がy=xと交点を持つ円を描き、交点の一つをPとします。

▲図2.線分ABを弦とする円を描きました
このとき、直線y=xの点A、Bと反対側の円周上に点Qをとることができ、∠APBと∠AQBは弧ABに対しての円周角なので、∠APB=∠AQBです。
次に、点Aと点Qを結んだ直線と直線y=xとの交点をP’とすると、∠AP’B>∠AQB(∠AP’B=∠AQB+∠P’BQ)で、∠AP’B>∠APBになります。
つまり、線分ABを弦とする円の弧が、直線y=xの点A、Bと反対側にあるとき、∠AQB=∠APBとなる点Qをとることができ、そのとき、∠AP’B>∠APBなので、∠APBは最大ではありません。∠APBが最大になるのは、点Qを取れないときで、それは円が直線y=xに接するときになり、このとき接点がPになります。

▲図3.線分ABを弦とする円と直線y=xの接点がPのとき、∠APBは最大になります
このとき、直線BPは、傾き-1、切片2の直線で、それはy=-x+2です。これとy=xの交点Pは、(1,1)になります。
したがって、△ABPは、∠BAP=90°の直角二等辺三角形になり、∠APBの最大値は45°=π/4で、これが答えです。
続いて、三角関数を利用して解いてみましょう。
図4の△ABPで、∠APB=θとします。

▲図4.三角関数を利用します
まず初めに、θの範囲を調べましょう。
点Pが直線y=x上を原点に近づいていくと、θは0に近づきます。
また、図5のように線分ABを直径とする円を考えたとき、この円周上の点をQとすると、∠AQB=90°で、さらに、この円周と直線y=xは交点を持たないので、θ<∠AQB=90°です。

▲図5.θ<90°です
以上から、0<θ<90°になります。
次に余弦定理を使って、cosθを表すと、
cosθ=(PA^2+PB^2-AB^2)/(2PA・PB)
です。
これに
PA=√(x^2+(x-1)^2)
PB=√(x^2+(x-2)^2)
AB=1
を代入すると、
cosθ=((x^2+(x-1)^2)+(x^2+(x-2)^2)-1)/2√((x^2+(x-1)^2)(x^2+(x-2)^2)
=(2x^2-3x+2)/√((2x^2-2x+1)(2x^2-4x+4))
=√((4x^4-12x^3+17x^2-12x+4)/(4x^4-12x^3+18x^2-12x+4))
です。
これを見ると大変複雑な式になってしまいましたが、t=x+1/xとすると、x^2+1/x^2=t^2-2なので、
cosθ=√((4t^2-12t+9)/(4t^2-12t+10))
=√(1-1/(4t^2-12t+10))
と簡単な式にすることができます。
ここでちょっと、θとcosθの関係を調べておくと、0<θ<90°でcosθは単調に減少するので、θが最大になるとき、cosθは最小になります。これは、1-1/(4t^2-12t+10)が最小になるとき、つまり、4t^2-12t+10が最小になるとき、θは最大値となるということです。
次に、tの取り得る範囲を調べておくと、t=x+1/xなので、相加相乗平均の関係から、t=x+1/x≧2√(x・1/x)=2(等号はx=1のとき成り立ちます)です。
以上から、t≧2の範囲で、4t^2-12t+10が最小になるとき、θは最大値となるということです。
そこで、
4t^2-12t+10=4(t^2-3)+10
=4((t-3/2)^2-9/4)+10
=4(t-3/2)^2+1
と変形すると、t≧2の範囲で4t^2-12t+10が最小になるのは、t=2のときです。
このとき、
cosθ=√(1-1/(16-24+10))
=√(1-1/2)
=1/√2
なので、θ=45°=π/4で、図形から導いた答えと一致しました。
三角関数は高校で勉強しますが、興味のある人は調べてみてください。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます