算額(その521)
岩手県一関市 菅原神社 嘉永3年(1850)
一関市博物館>>和算に挑戦>>平成19年度出題問題&解答例>>平成19年度出題問題(2)[中級問題] https://www.city.ichinoseki.iwate.jp/museum/wasan/h19/normal.html
正方形の中に四分円 3 個と等円 2 個が入っている。等円の直径が 1 のとき,正方形の一辺の長さを求めよ。また,斜線部分の面積を求めよ。
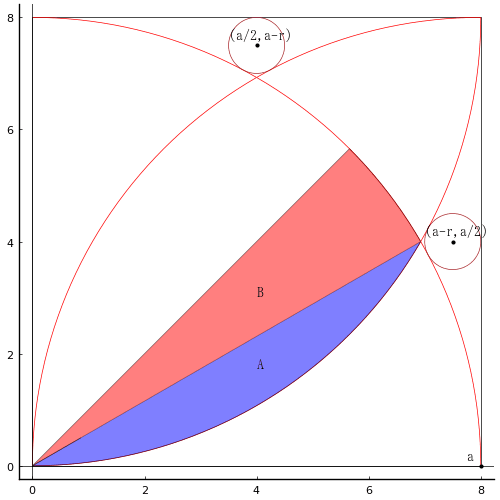
等円の半径と正方形の一辺の長さを r, a とおき,以下の方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, r::positive;
eq = (a/2)^2 + (a - r)^2 - (a + r)^2
solve(eq, a)[1] |> println
16*r
r = 1/2 のとき,正方形の一辺の長さは 8 である。
求めるべき面積は A, B の和の 2 倍である。
A は半径 a の面積の 15/360 である。
B は半径 a の面積の 1/6 から,一辺の長さが a の正三角形の面積を差し引いたものである。
a = 8
A = PI*a^2*(15//360)
B = PI*a^2/6 - a*(a//2)√Sym(3)/2;
求める面積は (80π - 96√3)/3 = 28.3501782535237 である。
2(A + B) |> simplify |> println
-32*sqrt(3) + 80*pi/3
2(A + B).evalf()
28.3501782535237
function fill(a)
x = vcat(a.*cosd.(270:330), [0])
y = vcat(a.*sind.(270:330) .+ a, [0])
plot!(x, y, color=:black, lw=0.5, seriestype=:shape, fillcolor=:blue, alpha=0.5)
x = vcat(a.*cosd.(30:45), [0, cosd(30)])
y = vcat(a.*sind.(30:45), [0, sind(30)])
plot!(x, y, color=:black, lw=0.5, seriestype=:shape, fillcolor=:red, alpha=0.5)
end;
function draw(r, n, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(a, r) = (8, 1//2)
@printf("正方形の一辺の長さ = %g; 等円の半径 = %g\n", a, r)
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:black, lw=0.5)
circle(0, 0, a, beginangle=0, endangle=90)
circle(a, 0, a, beginangle=90, endangle=180)
circle(0, a, a, beginangle=270, endangle=360)
circle(a/2, a-r, r, :brown)
circle(a - r, a/2, r, :brown)
fill(a)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(0.5a, 0.24a, "A", :black, mark=false)
point(0.5a, 0.4a, "B", :black, mark=false)
point(a/2, a - r, " (a/2,a-r)", :black, :center, :bottom, delta=delta/2)
point(a - r, a/2, " (a-r,a/2)", :black, :center, :bottom, delta=delta/2)
point(a, 0, "a ", :black, :right, :bottom, delta=delta/2)
end
end;