算額（その498）

算額（その498）

埼玉県北本市本宿 天神社 明治24年(1891)

北本デジタルアーカイブズ 北本市史 通史編 近世
https://kdas.jp/detail_display.php?t_cd=1&acc_cd=1&aclc_cd=40&chap=3&hp_page=47&bc_cd=1

この算額は，算額（その269）
https://blog.goo.ne.jp/r-de-r/e/1fd7e974eb24c0c5118e308a9e790003
のものと類似している。
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額（260）
長野県下高井郡木島平村 天満宮 推定明治21年(1888)

両者が異なる点は，
天満宮（その269）のものは，小円が中円 2 個と大円 1 個に外接するが
天神社のものは，小円が中円 3 個と外接する点である。

天神社のものは天満宮（その269）のものより3年後のものなので，問の写し間違いがあったのかもしれない。

大円 2 個，中円 5 個，小円 4 個が配置されている。小円は 3 個の中円に外接している。
大円の直径が 2 寸 8 分のとき，小円の直径を求めよ。

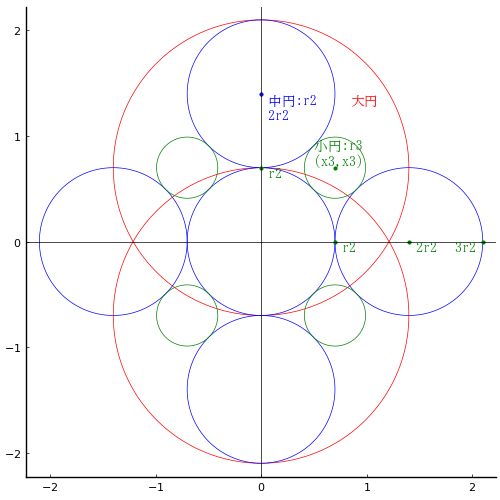
大円，中円の半径を r1, r2 とおく（r2 = r1/2）。小円の直径を r3, 中心座標を (x3, x3) とおき，以下の方程式を解く。条件式が 2 本で，r3, x3 の二変数について解を求める。その解の式には r1 が変数として含まれる。

なお，x3 = r1/2 は図が正しければ自明だが，一応，未知数として解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, r3::positive, x3::positive;

r2 = r1//2
eq1 = 2x3^2 - (r2 + r3)^2
eq2 = (2r2 - x3)^2 + x3^2 - (r2 + r3)^2;

solve([eq1, eq2], (r3, x3))

   1-element Vector{Tuple{Sym, Sym}}:
    (r1*(-1/2 + sqrt(2)/2), r1/2)

ここで面白いことに気づいた。
天満宮の算額（その269）では，SymPy で計算した小円の半径が 「3*r1/14」 になったのに，術では「r1*(sqrt(1/2) - 1/2)」としており不一致であった。
そして，天神社の算額（その498）の術は SymPy で計算した通りの「r1*(sqrt(1/2) - 1/2)」である。
天満宮の算額は，答えも術も正しいが図が間違えていたということで，本来同じ問であった（天神社のものは問，図，答，術すべてが正しい）ということである。

直径が 2.8 寸ならば，小円の直径は (sqrt(1/2) - 1/2)*2.8 = 0.5798989873223331 である。

ここで，今度は天神社の答えが間違っている。(sqrt(1/2) - 1/2)*2.8 を計算した結果が 0.574 に切り捨てられている。

(sqrt(1/2) - 1/2)*2.8

   0.5798989873223331

   r3 = 0.289949;  x3 = 0.700000
   小円の直径 = 2r3 = 0.579899

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 28//20  # 半径が 1.4 寸のとき
   r2 = r1//2
   (r3, x3) = (r1*(-1/2 + sqrt(2)/2), r1/2)
   @printf("r3 = %.6f;  x3 = %.6f\n", r3, x3)
   @printf("小円の直径 = 2r3 = %.6f\n", 2r3)
   plot()
   circle(0, r2, 2r2)
   circle(0, -r2, 2r2)
   circle(0, 0, r2, :blue)
   circle42(0, 2r2, r2, :blue)
   circle4(x3, x3, r3, :green)
   if more
       point(r2, 0, " r2")
       point(0, r2, " r2")
       point(2r2, 0, " 2r2")
       point(0, 2r2, " 中円:r2\n 2r2", :blue)
       point(3r2, 0, "3r2 ", :green, :right)
       point(x3, x3, " 小円:r3\n (x3,x3)", :green, :center, :bottom)
       point(1.2r2, 2r2, "大円", :red, mark=false)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その497）

算額（その497）

埼玉県さいたま市中央区円阿弥 日枝神社 慶応2年(1866) 正野友三郎一門奉納の算額

与野郷土資料館 展示Web解説（その21）
https://www.city.saitama.jp/004/005/004/005/yono/yonokyodo_tenjikaisetsu/p078011.html

外円の中に2個の三角形と甲円が 2 個，乙円が 6 個入っている。乙円の直径が 1 寸のとき，甲円の直径はいかほどか。

外円の半径と中心座標を r0, (0, 0)
甲円の半径と中心座標を r1, (0, r2 + r1)
乙円の半径と中心座標を r2, (x2, y2), (r0 - r2, 0)
とおき，以下の連立方程式を解く。

ただし，一度に解くと solve() の能力的に解けないことと，数値解を求める場合にも収束が不安定になるので，まずは外円と甲円の r0, r1 を先に求める。

include("julia-source.txt");

using SymPy

@syms r0::positive, r1, r2, x2, y2;

x = sqrt(r0^2 - r2^2)
eq1 = r0*x - (r0 - 2r2)sqrt(x^2 + (r0 - r2)^2)
eq2 = (sqrt(r0^2 - r2^2) + sqrt(r0^2 - r2^2 + (r0 - r2)^2))r1 - sqrt(r0^2 - r2^2)*(r0 - r2);
res1 = solve([eq1, eq2], (r0, r1))

   2-element Vector{Tuple{Sym, Sym}}:
    (r2, r1)
    (8*r2, 3*r2)

解は 2 通り求まるが 2 番目のものが適解である。
すなわち，外円の半径は乙円の半径の 8 倍，甲円の半径は乙円の半径の 3 倍である。
乙円の直径が 1 寸のとき，外円の直径は 8 寸，甲円の直径は 3 寸である。

算額の問の答えとしては以上で十分であるが，図形を描くために右上にある乙円の中心座標を求める。

@syms r0, r1, r2, x2, y2;

(r0, r1) = (8r2, 3r2)
eq3 = y2*r0/(x2*sqrt(r0^2 - r2^2)) - 1
eq4 = x2^2 + y2^2 - (r0 - r2)^2
res2 = solve([eq3, eq4], (x2, y2))

   2-element Vector{Tuple{Sym, Sym}}:
    (-56*sqrt(127)*r2^2/(127*sqrt(r2^2)), -21*sqrt(889)*r2/127)
    (56*sqrt(127)*r2^2/(127*sqrt(r2^2)), 21*sqrt(889)*r2/127)

解は 2 通り求まるが 2 番目のものが適解である。

乙円の直径が 1 寸のとき，
甲円の直径 = 3;  外円の直径 = 8
r0 = 4;  r1 = 1.5;  r2 = 0.5;  x2 = 2.4846;  y2 = 2.46511 である。

using Plots

function draw(r2, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, r1) = (8*r2, 3*r2)
   (x2, y2) = (56*sqrt(127)*r2^2/(127*sqrt(r2^2)), 21*sqrt(889)*r2/127)
   @printf("甲円の直径 = %g;  外円の直径 = %g;  r0 = %g;  r1 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n",
       2r1, 2r0, r0, r1, r2, x2, y2)
   x = sqrt(r0^2 - r2^2)
   plot([x, 0, -x, x], [r2, r0, r2, r2], color=:red, lw=0.5)
   plot!([x, 0, -x, x], -[r2, r0, r2, r2], color=:red, lw=0.5)
   circle(0, 0, r0, :gray)
   circle(0, r2 + r1, r1, :blue)
   circle(0, -r2 - r1, r1, :blue)
   circle4(x2, y2, r2, :green)
   circle(r0 - r2, 0, r2, :green)
   circle(r2 - r0, 0, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, r2 + r1, " 甲円:r1\n (0,r2+r1)", :blue, :left, :vcenter)
       point(x2, y2, "乙円:r2,(x2,y2)", :green, :center, :bottom, delta=delta/2)
       point(r0 - r2, 0, "r0-r2", :green, :center, :bottom, delta=delta/2)
       point(r0, 0, " r0", :black, :left, :bottom, delta=delta/2)
       point(r0, 0, " r0", :black, :left, :bottom, delta=delta/2)
       point(x, r2, "(√(r0^2-r2^2),r2)  ", :red, :right, :bottom, delta=delta/2)
       point(0, r2, " r2", :green, :left, :bottom, delta=delta/2)
   else
       plot!(showaxis=false)
   end
end;