ブルー・ムーン

これぞまことのブルー・ムーン

算額（その483）

算額（その483）

宮城県丸森町小斎日向 鹿島神社 明治41年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

団扇形内に甲円 2 個，乙円 5　個が入っている。扇形の直径（外円の直径）を与えて乙円の直径を求めよ。

不思議な問である。甲円や左右にある乙円は何の情報も与えない。外円の直径の上に 6 個の乙円があるので，乙円の直径は外円の直径の 1/6 である。

以下は図を描くためにすべての円の直径および中心座標を連立方程式を立てて解く。
甲円は外円に内接し，真ん中の乙円と外接している。

外円の半径と中心座標を r0, (0, 0); r0 = 6r2
甲円の半径と中心座標を r1, (x1, r1)
乙円の半径と中心座標を r2, (0, 3r2), (x2, -r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r0::positive, r1::positive, x1::positive,
     r2::positive, x2::positive;

r2 = r0//6
eq1 = x1^2 + r1^2 - (r0 - r1)^2
eq2 = x1^2 + (3r2 - r1)^2 - (r1 + r2)^2
eq3 = x2^2 + r2^2 - (r0 - r2)^2
res = solve([eq1, eq2, eq3], (r1, x1, x2))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (11*r0/30, 2*sqrt(15)*r0/15, sqrt(6)*r0/3)

r0 = 3 のとき，乙円の直径は 1，甲円の直径は 2.2

   r0 = 3;  r1 =　1.1;  r2 =　0.5;  x1 =　1.54919;  x2 = 2.44949
   乙円の直径 = 1

using Plots

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r0 = 3
   (r1, x1, x2) = (11*r0/30, 2*sqrt(15)*r0/15, sqrt(6)*r0/3)
   r2 = r0/6
   @printf("r0 = %g;  r1 =　%g;  r2 =　%g;  x1 =　%g;  x2 = %g\n",  r0, r1, r2, x1, x2)
   @printf("乙円の直径 = %g\n", 2r2)
   plot()
   circle(0, 0, r0, :black)
   circle(x1, r1, r1, :blue)
   circle(-x1, r1, r1, :blue)
   circle(0, r2, r2, :green)
   circle(0, 3r2, r2, :green)
   circle(0, 5r2, r2, :green)
   circle(x2, -r2, r2, :green)
   circle(-x2, -r2, r2, :green)
   circle(0, -r0, r0, beginangle=30, endangle=150) 
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(x1, r1, "甲円:r1,(x1,r1)", :blue, :center, :top, delta=-delta)
       point(0, 3r2, " 乙円:r2,(0,3r2)", :green, :left, :vcenter)
       point(x2, -r2, "乙円:r2,(x2,-r2) ", :green, :right, :vcenter)
       point(0, 6r2, " r0=6r2", :green, :left, :bottom, delta=delta/2)
   else
       plot!(showaxis=false)
   end
end;

算額（その482）

算額（その482）

宮城県丸森町小斎日向 鹿島神社 明治13年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

外円内に甲円 1 個と，乙円，大円，小円，1/3 円弧が各 2 個入っている。
小円の直径が 111 寸のときに，乙円の直径を求めよ。

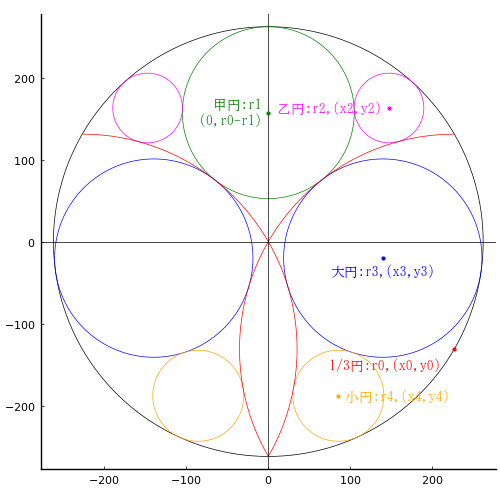
1/3 円の半径は外円の半径と同じ長さである。
外円の半径と中心座標を r0, (0, 0)
甲円の半径と中心座標を r1, (0, r0 - r1)
乙円の半径と中心座標を r2, (x2, y2)
大円の半径と中心座標を r3, (x3,y3)
小円の半径と中心座標を r4, (x4, y4)
1/3円の半径と中心座標を r0, (x0, y0), (-x0, y0); x0 = r0*cosd(30), y0 = -r0*sind(30)
とおき，以下の連立方程式を nlsolve() で解き，数値解を求める。

include("julia-source.txt");

using SymPy

@syms r0::positive, x0::positive, y0::positive, r1::positive,
      r2::positive, x2::positive, y2::positive,
      r3::positive, x3::positive, y3::negative,
      r4::positive, x4::positive, y4::negative;

(x0, y0) = r0 .* (cosd(Sym(30)), -sind(Sym(30)))
eq1 = x2^2 + y2^2 - (r0 - r2)^2
eq2 = x3^2 + y3^2 - (r0 - r3)^2
eq3 = x4^2 + y4^2 - (r0 - r4)^2
eq4 = x2^2 + (r0 - r1 - y2)^2 - (r1 + r2)^2
eq5 = x3^2 + (r0 - r1 - y3)^2 - (r1 + r3)^2
eq6 = (x2 - x0)^2 + (y2 - y0)^2 - (r2 + r0)^2
eq7 = (x0 - x3)^2 + (y0 - y3)^2 - (r0 - r3)^2
eq8 = (x3 + x0)^2 + (y3 - y0)^2 - (r0 + r3)^2
eq9 = (x4 + x0)^2 + (y4 - y0)^2 - (r0 + r4)^2
eq10 = (x3 - x4)^2 + (y3 - y4)^2 - (r3 + r4)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9, eq10], (r0, r1, r2, x2, y2, r3, x3, y3, x4, y4))

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r0, r1, r2, x2, y2, r3, x3, y3, x4, y4) = u
   return [
       x2^2 + y2^2 - (r0 - r2)^2,  # eq1
       x3^2 + y3^2 - (r0 - r3)^2,  # eq2
       x4^2 + y4^2 - (r0 - r4)^2,  # eq3
       x2^2 - (r1 + r2)^2 + (r0 - r1 - y2)^2,  # eq4
       x3^2 - (r1 + r3)^2 + (r0 - r1 - y3)^2,  # eq5
       (r0/2 + y2)^2 - (r0 + r2)^2 + (-sqrt(3)*r0/2 + x2)^2,  # eq6
       (-r0/2 - y3)^2 - (r0 - r3)^2 + (sqrt(3)*r0/2 - x3)^2,  # eq7
       (r0/2 + y3)^2 - (r0 + r3)^2 + (sqrt(3)*r0/2 + x3)^2,  # eq8
       (r0/2 + y4)^2 - (r0 + r4)^2 + (sqrt(3)*r0/2 + x4)^2,  # eq9
       -(r3 + r4)^2 + (x3 - x4)^2 + (y3 - y4)^2,  # eq10
   ]
end;

r4 = 111/2
iniv = [big"262.1", 104.8, 42.5, 147.2, 162.9, 121.0, 139.7, -20.2, 85.4, -188.1] .* (2r4/111)
res = nls(H, ini=iniv);
println(res);

   (BigFloat[262.0833333333333172109930603571207271282688760651230918115043361933301448197767, 104.8333333333333223290545431295149542914840906048369827515914261371678084910254, 42.49999999999999786805343180884086908114509397785038194649776129778549724683521, 147.2243186433545568780056630764879738313623588458994394289193799498887306062796, 162.9166666666666596227807113723227255431557568042764514701570712819220452794033, 120.9615384615384515366858225567229155263396173464548862680437593159638153814604, 139.6743535847209988034369530154419060452378981480626331409871051079048418882699, -20.16025641025639136090801019725193623031123311832732180465654678920082881995361, 85.44783984006462676161828043480466817900534748463440517739428912144201840260664, -188.0833333333333094401143692287399234355784895913830835735564890504723176520062], true)

乙円の直径は 85 寸である。

   r0 = 262.083;  r1 =　104.833
   r2 =　42.5;  x2 =　147.224;  y2 = 162.917
   r3 =　120.962;  x3 =　139.674;  y3 =　-20.1603
   r4 = 55.5;  x4 = 85.4478;  y4 = -188.083
   乙円の直径 = 85

using Plots

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r4 = 111/2
   (r0, r1, r2, x2, y2, r3, x3, y3, x4, y4)  = res[1]
   (x0, y0) = r0 .* (cosd(30), -sind(30))
   @printf("r0 = %g;  r1 =　%g\nr2 =　%g;  x2 =　%g;  y2 = %g\nr3 =　%g;  x3 =　%g;  y3 =　%g\nr4 = %g;  x4 = %g;  y4 = %g\n",  r0, r1, r2, x2, y2, r3, x3, y3, r4, x4, y4)
   @printf("乙円の直径 = %g\n", 2r2)
   plot()
   circle(0, 0, r0, :black)
   circle(0, r0 - r1, r1, :green)
   circle(x2, y2, r2, :magenta)
   circle(x3, y3, r3, :blue)
   circle(-x3, y3, r3, :blue)
   circle(x4, y4, r4, :orange)
   circle(-x4, y4, r4, :orange)
   circle(x0, y0, r0, :red, beginangle=90, endangle=210)
   circle(-x0, y0, r0, :red, beginangle=-30, endangle=90)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, r0 - r1, "甲円:r1 \n(0,r0-r1) ", :green, :right, :vcenter)
       point(x2, y2, "乙円:r2,(x2,y2) ", :magenta, :right, :vcenter)
       point(x3, y3, "大円:r3,(x3,y3)", :blue, :center, :top, delta=-delta)
       point(x4, y4, " 小円:r4,(x4,y4)", :orange, :left, :vcenter)
       point(x0, y0, "1/3円:r0,(x0,y0)  ", :red, :right, :top, delta=-1.5delta)
   else
       plot!(showaxis=false)
   end
end;