算額(その98)
元の「算額その(98)」の改訂版である
東京都渋谷区渋谷 金王八幡神社 安政6年(1859)4月
https://gunmawasan.web.fc2.com/files/konnou-HP.pdf
金王八幡宮③「宝物館」(渋谷散歩③)
https://wheatbaku.exblog.jp/30049403/
一部が欠けている円内に円弧を置き,甲円 1 個,乙円 3 個を入れる。甲円,乙円の直径がそれぞれ 5 寸,4 寸のとき,円弧の弦の長さはいくらか。
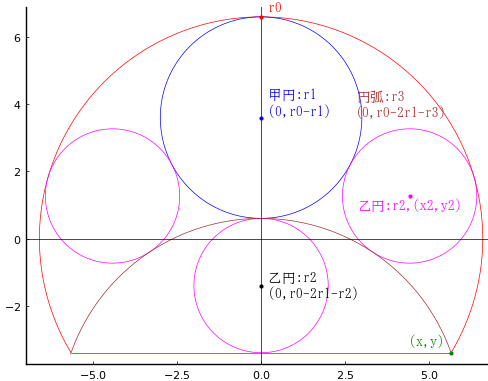
外円の半径と中心座標を r0, (0, 0)
甲円の半径と中心座標を r1, (0, r0 - r1)
乙円の半径と中心座標を r2, (x2, y2)
円弧の一部になる円の半径と中心座標を r3, (0, r0 - 2r1 - r3)
外円と円弧の交点座標を (x, y)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms r0::positive, r1::positive, r2::positive, x2::positive,
y2::positive, r3::positive;
y = r0 - 2r1 - 2r2
x = sqrt(r0^2 - y^2)
eq1 = x2^2 + y2^2 - (r0 - r2)^2
eq2 = x2^2 + (r0 - r1 - y2)^2 - (r1 + r2)^2
eq3 = x2^2 + (y2 -(r0 - 2r1 - r3))^2 - (r2 + r3)^2
eq4 = (r0^2 - y^2) + (r3 - 2r2)^2 - r3^2
res = solve([eq1, eq2, eq3, eq4], (r0, x2, y2, r3))
1-element Vector{NTuple{4, Sym}}:
(r1*(r1^2 + r1*r2 - r2^2)/((r1 - r2)*(r1 + r2)), r2*sqrt(4*r1^2 + 4*r1*r2 - 4*r2^2)/r1, -(r1^4 - 3*r1^2*r2^2 - r1*r2^3 + 2*r2^4)/(r1*(r1 - r2)*(r1 + r2)), r1*r2/(r1 - r2))
x の根号の中身 r0^2 - (r0 - 2*r1 - 2*r2)^2 の x0 に
r0 = r1*(r1^2 + r1*r2 - r2^2)/((r1 - r2)*(r1 + r2))
を代入する。
r0 = r1*(r1^2 + r1*r2 - r2^2)/((r1 - r2)*(r1 + r2))
r0^2 - (r0 - 2*r1 - 2*r2)^2 |> simplify |> println
4*r2^3/(r1 - r2)
甲円と乙円の半径がそれぞれ r1 = 5/2, r2 = 4/2 のとき,弦の長さは 2sqrt(4*r2^3/(r1 - r2)) = 16 である。
draw(5/2, 4/2, true)
r1 = 2.5; r2 = 2; r0 = 8.05556; x2 = 4.30813; y2 = 4.25556; r3 = 10
x = 8; y = -0.944444; 弦の長さ = 2x = 16
2sqrt(4*r2^3/(r1 - r2)) |> simplify |> println
4*r2^(3/2)*sqrt(1/(r1 - r2))
術で言う「弦は 2乙 / sqrt(甲/乙 - 1)」と同じである(甲=2r1, 乙=2r2)。
4r2/sqrt(2r1/2r2 - 1) |> simplify |> println
4*r2^(3/2)/sqrt(r1 - r2)
function draw(r1, r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="")#, fontfamily="IPAMincho")
(r0, x2, y2, r3) = (r1*(r1^2 + r1*r2 - r2^2)/((r1 - r2)*(r1 + r2)), r2*sqrt(4*r1^2 + 4*r1*r2 - 4*r2^2)/r1, -(r1^4 - 3*r1^2*r2^2 - r1*r2^3 + 2*r2^4)/(r1*(r1 - r2)*(r1 + r2)), r1*r2/(r1 - r2))
@printf("r1 = %g; r2 = %g; r0 = %g; x2 = %g; y2 = %g; r3 = %g\n", r1, r2, r0, x2, y2, r3)
y = r0 - 2r1 - 2r2
x = sqrt(r0^2 - y^2)
θ = round(atand(y/x))
yy = y - (r0 - 2r1 - r3)
θ2 = round(atand(yy/x))
@printf("x = %g; y = %g; 弦の長さ = 2x = %g\n", x, y, 2x)
plot()
circle(0, 0, r0, :red, beginangle=θ, endangle=180 - θ)
circle(0, r0 - r1, r1, :blue)
circle(0, r0 - 2r1 - r2, r2, :magenta)
circle(x2, y2, r2, :magenta)
circle(-x2, y2, r2, :magenta)
circle(0, r0 - 2r1 - r3, r3, :brown, beginangle=θ2, endangle=180 - θ2)
segment(-x, y, x, y, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(x, y, "(x,y) ", :green, :right, :bottom, delta=delta)
point(0, r0 - r1, " 甲円:r1\n (0,r0-r1)", :blue, :left, :bottom)
point(x2, y2, "乙円:r2,(x2,y2)", :magenta, :center, :top, delta=-delta/2)
point(0, r0 - 2r1 - r2, " 乙円:r2\n (0,r0-2r1-r2)", :black, :left, :vcenter)
point(0, r0, " r0", :red, :left, :bottom, delta=delta/2)
point(x/2, -1.3y, "円弧:r3\n(0,r0-2r1-r3)", :brown, mark=false)
end
end;
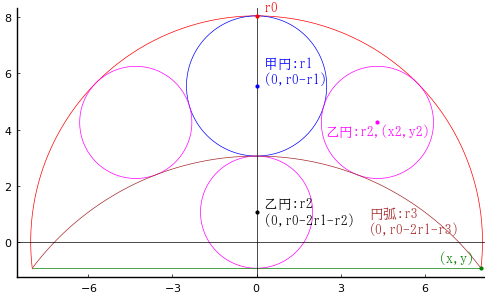
draw(6/2, 4/2, true)
r1 = 3; r2 = 2; r0 = 6.6; x2 = 4.42217; y2 = 1.26667; r3 = 6
x = 5.65685; y = -3.4; 弦の長さ = 2x = 11.3137