マッキーの一問必答（９）：二等辺三角形の性質を利用する問題（１）

ブログ人気投票にクリックいただけると幸いです！


　「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む２６年度の問題を取り上げ、ポイントを解説します。

　前回に引き続いて、中学入試問題の図形問題で、経験的に覚えていなければならない問題を取り上げ解説します。学校では小学４年生で学習する、二等辺三角形の性質を使う問題を、今回と次回の二回に分けて説明しましょう。

　学校で学習する二等辺三角形の性質を問う入試問題は、頻出問題と言えるほど、今回取り上げた学校以外にも多くの学校で出題されています。


【２６年度の入試問題】　（分数の表記および記号が、実際の入試問題と若干異なります。）

　今回は、高輪中学校・品川女子学院中等部・横浜雙葉中学校の入試問題を取り上げます。


１．高輪中学校

下の図のように、正三角形ＡＢＣの辺ＢＣをのばした直線と、頂点Ａを通る直線が、点Ｅで交わっています。また、ＡＣ＝ＣＤ＝ＤＥです。図の（あ）の角の大きさは何度ですか。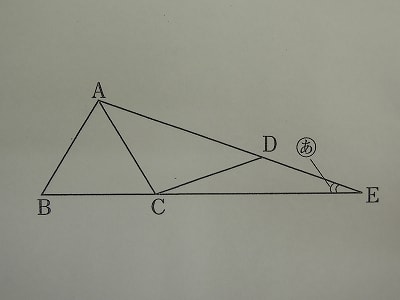




２．品川女子学院中等部

次の図で角アは角イの４倍の大きさで、辺ＢＣ，ＣＤ，ＤＥ，ＥＦの長さは等しいです。三角形ＡＥＦが二等辺三角形であるとき、角ウの大きさは□°です。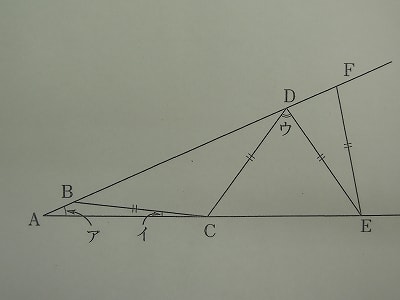




３．横浜雙葉中学校

下の図の三角形ＡＢＣはＡＢ＝ＡＣの二等辺三角形で、角アは７５度、ＢＣ＝ＢＦ＝ＥＦ，ＡＤ＝ＤＥです。イの角度は何度ですか。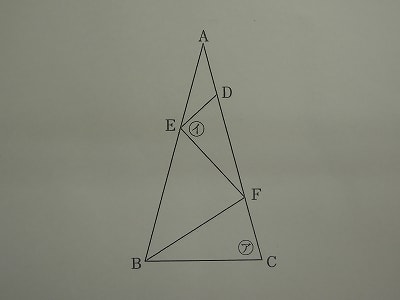




【解答と理解しておくべきポイント】

二等辺三角形の定義は、　「二つの辺の長さが等しい三角形」です。山の形の頂上の角を頂角、下の二つの角を底角と言います。二等辺三角形は、２辺の長さが等しいだけではなく、２つの底角の大きさが等しくなります。

また、頂角の大きさが定まると、残りの底角の大きさが決まり、一つの底角の大きさが定まると、残りの底角および頂角の大きさが決まります。


まず、高輪中学校の問題から解説します。

高輪の算数は、問題１に計算４題、問題２が小問４題、その後それぞれ小問が３つずつある大問が３題出題されました。今回の問題は、問題２の小問の一つです。

この種の問題は、二等辺三角形の底角が等しいという性質と、三角形の外角の定理を上手く使って求める、基本的な問題です。

下の図のように、最も小さな底角Ｅの大きさを①と置きます。三角形ＤＣＥの外角ＡＤＣは、角Ｅと角ＤＣＥの和となりますから、その大きさは②です。

同様に三角形ＡＣＥの外角ＢＣＡは、角Ｅと角ＥＡＣの和ですから、その大きさは③と表すことが出来ます。

三角形ＡＢＣは正三角形ですので、角ＢＣＡ＝６０度＝③

よって求める（あ）の角の大きさは、①ですので、６０÷３＝２０度




次は品川女子の問題です。

品川女子の算数の問題は、問題１が計算２題、問題２が小問６題、それに小問が２題ずつある大きな問題が４題で構成されています。今回の問題は、問題２の小問の一つです。

条件の「角アは角イの４倍の大きさ」から、角イをもとにしていますので、角イの大きさを①と置きます。すると角アの大きさは④となります。

高輪中学と同様に、二等辺三角形の性質と、三角形の外角の定理を使って、それぞれの角の大きさを下の図のように表してみます。

三角形ＡＥＦが二等辺三角形であるなら、頂角の大きさが④で、底角の大きさが⑬と表すことができます。

よって、④＋⑬×２＝１８０という式が出てきます。

マル３０＝１８０度ですので　①＝６度

よって求める角ウの大きさは、
１８０－（⑤＋⑬）＝１８０－⑱＝１８０－６×１８＝７２度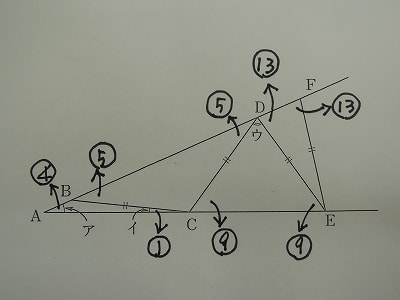




最後は、横浜雙葉の問題です。

横浜雙葉の算数は、問題１が計算を含む小問８題、問題２は小問４題・問題３が小問３題で構成された大問で作られています。

今回問題は、問題１の小問の一つとして出題されています。

条件を図に記入します。まず一番大切なことは、三角形ＡＢＣと三角形ＢＣＦは底角が共通の７５度ですから、相似な二等辺三角形であることに気づくことです。

頂角７５度の二等辺三角形の頂角の大きさは、
１８０－７５×２＝３０度
よって角Ａ＝３０度ですので、外角の定理より角ＥＤＦ＝３０×２＝６０度

また角ＥＢＦ＝角ＡＢＣ－角ＦＢＣ＝７５－３０＝４５度、
角ＢＦＥ＝１８０－４５×２＝９０度

このことから、角ＥＦＤ＝１８０－（７５＋９０）＝１５度
角イ＝１８０－（角ＥＤＦ＋角ＥＦＤ）＝１８０－（６０＋１５）＝１０５度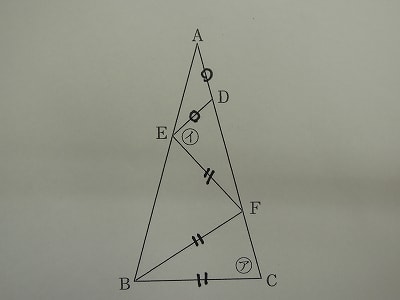



　以上の問題とその解法を理解すると、こうした問題に目が慣れて来るはずで、そうした経験が、新たな問題を考えるときに解き方のヒントになります。

　次回は、今回と同様に二等辺三角形の性質を使う問題ですが、少し変形された問題について考えてみましょう。