二重誤り訂正符号 (7)

記事一覧, sys.pdf, sys-s.pdf,

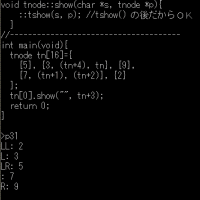
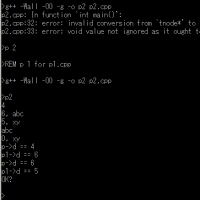
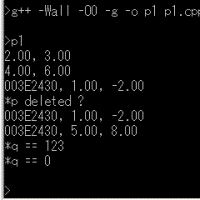
７．ユークリッド復号法

BCH符号のユークリッド復号法に関する解説をWeb上でも閲覧できます．ここでは文献[3]を参照しながら三重誤りを訂正するときの「例1」を簡単に紹介します．なお，文献[3]の記法は上記のものと少し異なりますが，そのまま引用します．「例1」は x⁴ + x + 1 の根αで作られた符号語長15の三重誤り訂正符号で，誤り多項式がe(z) = z + z⁴ + z⁶ の場合の処理を示しています．三重誤り訂正の場合のシンドローム多項式は

        S(z) = s₁ + s₂ z + …… + s₆ zx⁵    ( s_i = S(αⁱ), 1 ≦ i ≦ 6 )

で，誤り位置を調べる多項式は

        σ(z) = (1 - α^i₁ z)(1 - α^i₂ z)(1 - α^i₃ z)

です．ユークリッド復号法では基本方程式

        σ(z) S(z) + φ(z) z⁶ = η(z)

を構成する多項式の次数に着目して，ユークリッドの互除法で次数を削減していきます．例１に数値が詳しく示されていますが，計算内容は漸化式

       

 を用いて

         

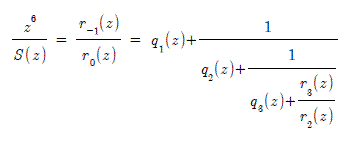
と連分数展開し，

       

と近似したものになっています．γ は γσ(0) = 1 とするための定数です．φ(z) や η(z) が表に出てこないのでよく分かりませんでした．e(z) = z という単一誤りのときのシンドローム多項式はS(z) = α + α² z + …… + α⁶ z⁵ であり

       

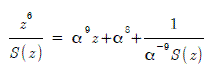
となって r₁(z) で次数が 0 になります．σ(z) = α^-9(α⁹ - α⁸ z) z² としたいのですが，そうではなくてσ(z) = α^-9(α⁹ - α⁸ z) とするのかも知れません．

ユークリッド復号法は[3]で詳しく解説されていますが，上記のような連分数展開による表現の方が覚えやすく，実際，Web上でも「BCH  連分数」や「BCH  continued fraction 」の検索で多数の資料が見つかります．参考までに IEEE Xplore Digital Library に示されている論文のアブストラクトを次に示します．

I. S. Reed and T. K. Truong,  
"Simple proof of the continued fraction algorithm for decoding Reed-Solomon codes"
Proceedings of the Institution of Electrical Engineers, December 1978
Abstract:
It was shown recently that BCH and RS codes can be implemented by Berlekamp's
algorithm using continued fraction approximations. A simple transparent proof
of Berlekamp's algorithm that uses such a development is given in this paper.

この記事は式が多いので B2012-06.odt を作成してから *.txt にコピーしてブログの記事にしました．ときどき式が抜けていたのはこのためです．B2012-06.odt の方がミスが少なく，これを *.pdf に変換して
  http://pulsar.blog.ocn.ne.jp/topics/B2012-06.pdf
に upload しています．