こんにちは。東久留米市の学習塾塾長です。
朝から雲が多く、昼前には雨が降り始めました。気温も16℃までしか上がらず寒い日になりそうです。風邪などひかぬよう暖かくして過ごしましょう。
さて、今回は2003年ジュニア数学オリンピックに出題された約数の問題を取り上げます。
問題は、
「1以上2003以下の整数のうち、正の約数の個数が偶数であるものはいくつあるか。
例えば、6の正の約数は1、2、3、6の4個なので、6はこの条件をみたしている。」
です。
早速、取り掛かりましょう。
ある整数Nが、

と素因数分解されるとき、Nの正の約数の個数は、
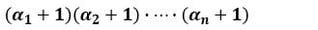 (*)
(*)
になります。(約数と式の展開)
このとき、Nが平方数の場合、α1、α2、・・・、αnは偶数なので、(*)は奇数になり、α1、α2、・・・、αnのなかで少なくとも1つ奇数がある場合(つまり、非平方数)、(*)は偶数になります。
これを利用すれば簡単です。
まず、1以上2003以下の整数のうちの平方数の個数を求めると、√2003=44.7・・・から、それは44個になります。
つまり、1以上2003以下の整数のうち、正の約数の個数が奇数のものは44個あり、それ以外のものは偶数です。
したがって、正の約数の個数が偶数のものは、2003-44=1959個で、これが答えです。
平方数と非平方数の約数の個数が、それぞれ奇数および偶数であることを知っていれば簡単な問題です。
朝から雲が多く、昼前には雨が降り始めました。気温も16℃までしか上がらず寒い日になりそうです。風邪などひかぬよう暖かくして過ごしましょう。
さて、今回は2003年ジュニア数学オリンピックに出題された約数の問題を取り上げます。
問題は、
「1以上2003以下の整数のうち、正の約数の個数が偶数であるものはいくつあるか。
例えば、6の正の約数は1、2、3、6の4個なので、6はこの条件をみたしている。」
です。
早速、取り掛かりましょう。
ある整数Nが、

と素因数分解されるとき、Nの正の約数の個数は、
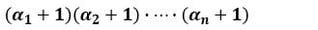 (*)
(*)になります。(約数と式の展開)
このとき、Nが平方数の場合、α1、α2、・・・、αnは偶数なので、(*)は奇数になり、α1、α2、・・・、αnのなかで少なくとも1つ奇数がある場合(つまり、非平方数)、(*)は偶数になります。
これを利用すれば簡単です。
まず、1以上2003以下の整数のうちの平方数の個数を求めると、√2003=44.7・・・から、それは44個になります。
つまり、1以上2003以下の整数のうち、正の約数の個数が奇数のものは44個あり、それ以外のものは偶数です。
したがって、正の約数の個数が偶数のものは、2003-44=1959個で、これが答えです。
平方数と非平方数の約数の個数が、それぞれ奇数および偶数であることを知っていれば簡単な問題です。










