算数においてひらめきと直感を引き出すには？

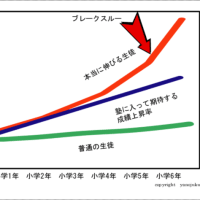
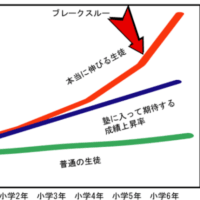
毎日、授業で子供たちの学習を見ていると、

子供たち一人ひとりが持っている個性によって

おおきく学習の結果が違ってくることが

わかります。

一定のレベルまでに

達したいと思ったら、あまりにその個性を

尊重しすぎてもいけません。なによりも

大切なことは、基礎トレーニングをしっかり

積むことです。それが、のちの入試に良い

結果をもたらしてくれます。

 

ＹＡＮＯ塾では小学生のほとんどが

中学受験を目標としています。

どの学年から始めても、

非受験型で基礎をしっかりと

積み上げていきます。

基礎から丁寧に学習を進めるには

訳があります。

 

急がばまわれという諺があるように

基礎、基本の勉強をやりながら、

問題を解くトレーニングをするのです。

 

算数ならば、問題を解くために

考えた式を丁寧に書いて、

さらにそれを式変形して

答えを導き出すことを

体に染み込ませます。

 

これは、いわゆる日本古来の

茶道、花道、武道の指導の仕方と同じです。

まず形がしっかり出来ていると、

そこに心が宿るわけです。

 

これは、学習も同じで、

正しい姿勢、考え方、

正しいノートの取り方、

曖昧さのない完全な理解によって

はじめて入試問題が解けるようなります。

 

その基礎・基本のカリキュラムがスムーズに進んで、

非受験型の模試で偏差値が６０以上、

点数で言うと９０点以上を

取れるようになったら、

受験型の中学受験コースに入っていきます。

 

入試問題にチャレンジするといっても、

最初は単元ごとに理解すべき内容と

解き方の公式をマスターしなければ

なりません。

 

和差算、差集め算、鶴亀算、流水算、比・割合、時計算、

図形問題、ニュートン算など

中学受験に必要な単元はたくさんありますが、

どの分野もつながりを持っています。

とくに線分図や面積図を使って解く問題は

それぞれ関連性を持っています。

 

上記のいくつかの算法の意味を理解し、

繰り返したくさんの問題を解くことが大切です。

ただ、無闇矢鱈にたくさんの問題を解くのではだめで、

徐々に問題の質とレベルを上げていくことが

大切です。

 

（そのあたりの進捗状態は

わたしが見ています。この指導で一番大切なことは

オーバーワーク、つまり問題のやり過ぎは禁物だということです。

あまりに大量の問題は心が折れてしまいます。

最初出来なかった問題が出来るようになれば、

褒めてあげることはとても効果が上がります。）

 

実は、この繰り返しで

身についたことが

入試において、実践的な

入試問題を解く際に大いに役立ちます。

 

入試問題になると、やはりそれを解くための

ひらめきというものが必要になります。

ところが、このひらめきですが、

直感という言葉と混同して使われます。

 

どちらも、日常でよく使う言葉ですが、

直感　と　ひらめき　

実は大きく違います。

 

ひらめきとは　理屈や論理に基づく判断から

考えつくことです。主に大脳皮質が受け持っています。

簡単に言うと、理詰めのことです。

算数・数学の問題を説いていて、

次に何をしていいか行き詰まることがありますね。

これは次の一手がひらめかない状態です。

 

 

詰将棋や算数の問題を解くためのプロセスは

だれでもが説明できることですよね。

一つ一つ、理詰めのステップを進めます。

しかしどこかで飛躍しないといけない局面に

きたとき、橋をかけないと進めない時があります。

その橋が、直感です。

 

この直感を育てるには脳科学者の池谷 裕二が

彼の著書　「「単純な脳、複雑な『私』」に

書いてあるのですが、

とにかく繰り返しが大切と

力説しています。

 

ただ、日常的に　「ひらめき」と

「直感」を同義に使っていることも

多いので、混乱してしまいがちです。

 

 

 

（この「ひらめき」と「直感」の定義は下で紹介している

脳科学の池谷裕二氏の著書

「単純な脳、複雑な『私』」から引用しています。

 

特に、算数・数学の弱い人はこの理詰めに

ついていけない人が多いですね。

もし理詰めに窮しているようでしたら、

ひらめきなどは夢の夢です。

 

どのようにしたらこの理詰めに強くなるかといえば、

結局はこの話の最初に述べましたように

基礎・基本をのところで、しっかりと

理解する。難しすぎる問題をしないで

基礎・基本の問題を１００％出来るようにすることです。

 

 

基礎・基本をしっかり身につけておけば、

簡単なところでのつまづきがなくなり、

きちんと問題を理解して、どうしても

飛躍しないと解けない問題でも

いままでの経験値から「ひらめき」が

働いて問題が解けるようになるのです。

 

こうなったらしめたものです。

ひらめきで問題が

解けるようになると、問題を解くのが

楽しくなります。

あとはこれを繰り返していけば、

「直感力」が育ち、

入試の難問にもひるまない

算数力がついてくるのです。

 

この伸びは生徒によってすごく違います。

もし伸びが良くないということであれば、

小学２年生から４年生にかけての

基礎・基本の習得が確実でないのかもしれません。

 

 

中学受験をすすめているのに、

学習の伸び悩みを抱えている人は

その部分で躓いている人が多いです。

ご心配な方は一度お気軽にご相談ください。

 

池谷さんの著書をご紹介します。

なかなか面白い本ですよ。

多感な小学生でも読めると思いますが、

中高生にもお勧めです。

もちろん子育て中の親御さんにも

とても参考になると思います。

 

	単純な脳、複雑な「私」 (ブルーバックス)
	池谷 裕二
	講談社