算額（その641）

算額（その641）

長野県飯田市 元善光寺 推定天保15年(1844)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

大小 2 個の正方形が接しており，正方形の頂点を結ぶ線分で分割された領域に，甲円，乙円，丙円を入れる。大小の正方形の面積の我が 113 平方寸，線分の長さが 17 寸のとき，2 個の正方形の一辺の長さ，甲円，乙円，丙円の直径を求めよ。

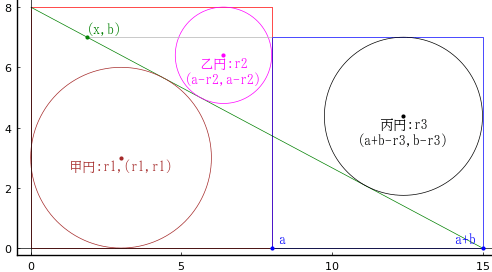
正方形の一辺の長さを a, b とする。
甲円の半径と中心座標を r1, (r1, r1)
乙円の半径と中心座標を r2, (a - r2, a - r2)
丙円の半径と中心座標を r3, (a + b - r3, b - r3)
とおき，以下の連立方程式を解く。なお，x は頂点を結ぶ線分と小さい方の正方形の上辺の延長線の交わる点の座標 (x, b) である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms A::positive, B::positive, a::positive, b::positive, x::positive, r1::positive, r2::positive, r3::positive

(A, B) = (113, 17)
eq1 = a + (a + b) - sqrt(a^2 + (a + b)^2) - 2r1
eq2 = a + (a - a*b/(a + b)) - sqrt(a^2 + (a - a*b/(a + b))^2) - 2r2
eq3 = (a + b - x) + b - sqrt((a + b - x)^2 + b^2) - 2r3
eq4 = a^2 + b^2 - A
eq5 = a^2 + (a + b)^2 - B^2
eq6 = b/(a + b - x) - (b - a*b/(a + b))/(a - x)
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (a, b, r1, r2, r3, x))

   2-element Vector{NTuple{6, Sym}}:
    (8, 7, 3, 8/5, 21/8, 15/8)
    (22*sqrt(5)/5, 9*sqrt(5)/5, -17/2 + 53*sqrt(5)/10, -187/31 + 583*sqrt(5)/155, -153/44 + 477*sqrt(5)/220, 403*sqrt(5)/110)

算額の問題を解くとき，解が複数個あるのは稀であるが，この問題においては，解は 2 組ある。
正方形の一辺の長さは (8, 7) （上図）

a = 8;  b = 7;  r1 = 3;  r2 = 1.6;  r3 = 2.625;  x = 1.875

と (22/√5, 9/√5) （下図）である。

a = 9.8387;  b = 4.02492;  r1 = 3.35116;  r2 = 2.37824;  r3 = 1.37093;  x = 8.19214

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b, r1, r2, r3, x) = res[n]
   @printf("a = %g;  b = %g;  r1 = %g;  r2 = %g;  r3 = %g;  x = %g\n", a, b, r1, r2, r3, x)
   plot()
   rect(0, 0, a, a, :red)
   rect(a, 0, a + b, b, :blue)
   segment(0, a, a + b , 0, :green)
   circle(r1, r1, r1, :brown)
   circle(a - r2, a - r2, r2, :magenta)
   circle(a + b - r3, b - r3, r3, :black)
   segment(x, b, a, b, :gray70)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(r1, r1, "甲円:r1,(r1,r1)", :brown, :center, delta=-delta/2)
       point(a - r2, a - r2, "乙円:r2\n(a-r2,a-r2)", :magenta, :center, delta=-delta/2)
       point(a + b - r3, b - r3, "丙円:r3\n(a+b-r3,b-r3)", :black, :center, delta=-delta/2)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(a + b, 0, "a+b ", :blue, :right, :bottom, delta=delta/2)
       point(x, b, "(x,b)", :green, :left, :bottom, delta=delta/2)
   end
end;

draw(1, true)
savefig("/Users/aoki/Downloads/fig1.png");

   a = 8;  b = 7;  r1 = 3;  r2 = 1.6;  r3 = 2.625;  x = 1.875


draw(2, true)
savefig("/Users/aoki/Downloads/fig2.png");

   a = 9.8387;  b = 4.02492;  r1 = 3.35116;  r2 = 2.37824;  r3 = 1.37093;  x = 8.19214


 

 

算額（その640）

算額（その640）

長野県伊達市羽広 仲仙寺 文政9年(1826)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

直角三角形内に累円（子円，丑円，寅円,…）が逐次内接し，累円と底辺の隙間に逐円（初円，二円，三円，…，終円）が入っている。初円の直径が 4 寸，終円の直径が 0.5 寸，逐円が 4 個（初円から数えて終円が 4 番目）のときに二円の直径はいかほどか。

子円の半径と中心座標を a0, (a0, a0)
丑円の半径と中心座標を a1, (xa1, a1)
寅円の半径と中心座標を a2, (xa2, a2)...
初円の半径と中心座標を b1, (xb1, b1)
二円の半径と中心座標を b2, (xb2, b2)...
とおき，以下の連立方程式により逐次，各円の半径と中心座標を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms 鈎::positive, 股::positive, 弦::positive,
     a0::positive
@syms xai::positive, ai::positive, xai1::positive, ai1::positive, bi1::positive, xbi1::positive

function func(ai, xai, 股)
   eq1 = (xai1 - xai)^2 + (ai - ai1)^2 - (ai + ai1)^2
   eq2 = (xbi1 - xai)^2 + (ai - bi1)^2 - (ai + bi1)^2
   eq3 = (xai1 - xbi1)^2 + (ai1 - bi1)^2 - (ai1 + bi1)^2
   eq4 = ai/(股 - xai) - ai1/(股 - xai1)
   return solve([eq1, eq2, eq3, eq4], (ai1, xai1, bi1, xbi1))
end

(鈎, 股) = (3, 6)
弦 = sqrt(鈎^2 + 股^2)
a0 = (鈎 + 股 - 弦)/2
println("弦 = $弦;  a0 = $a0")

   弦 = 6.708203932499369;  a0 = 1.1458980337503153

a = Vector{Float64}(undef, 10)
xa = Vector{Float64}(undef, 10)
b = Vector{Float64}(undef, 10)
xb = Vector{Float64}(undef, 10);

(a[1], xa[1], b[1], xb[1]) = func(a0, a0, 股)[1]
for i in 2:10
   (a[i], xa[i], b[i], xb[i]) = func(a[i - 1], xa[i -  1], 股)[1]
end

逐円の半径（直径）は初項 b[1]，公比 b[2]/b[1] の等比数列である（各項の対数を取るとすぐわかる）。
n 番目の逐円の半径は b[1]*(b[2]/b[1])^(n-1) である。

逆に，n 番目の逐円の半径がわかっているが公比がわかっていない場合に，公比 c は以下のようにして求めることができる。
逐円の個数を n，初円径を b1, 終円径を bn とする。

@syms b1, bn, n, c
res = solve(b1*c^(n - 1) - bn, c)[1] |> println

   (bn/b1)^(1/(n - 1))

二円の半径は b1*(bn/b1)^(1/(n - 1)) である。

逐円の個数が n = 4，初円径が b1 = 4, 終円径が bn = 0.5 とすると，公比は 0．5 で，二円の径は 2 である。

n = 4
b1 = 4
bn = 0.5
c = (bn/b1)^(1/(n - 1))
(c, b1*c)

   (0.5, 2.0)

function draw(more=false)
   pyplot(size=(700, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鈎, 股) = (4, 7)
   弦 = sqrt(鈎^2 + 股^2)
   a0 = (鈎 + 股 - 弦)/2
   a = Vector{Float64}(undef, 10)
   xa = Vector{Float64}(undef, 10)
   b = Vector{Float64}(undef, 10)
   xb = Vector{Float64}(undef, 10);
   (a[1], xa[1], b[1], xb[1]) = func(a0, a0, 股)[1]
   for i in 2:10
       (a[i], xa[i], b[i], xb[i]) = func(a[i - 1], xa[i -  1], 股)[1]
   end
   @printf("鈎 = %g;  股 = %g;  弦 = %g;  a0 = %g\n", 鈎, 股, 弦, a0)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:magenta, lw=0.5)
   circle(a0, a0, a0)
   for i in 1:10
       circle(xa[i], a[i], a[i])
       circle(xb[i], b[i], b[i], :blue)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       # vline!([0], color=:black, lw=0.5)
       # hline!([0], color=:black, lw=0.5)
       point(a0, a0, "子", :red, :center, :vcenter, mark=false)
       for (i, char) in enumerate(['丑', '寅', '卯', '辰'])
           point(xa[i], a[i], char, :red, :center, :vcenter, mark=false)
       end
       for (i, char) in enumerate(['初', '二', '三'])
           point(xb[i], b[i], char, :blue, :center, :vcenter, mark=false)
       end
   end
end;