算額(その616)
福島県白河市明神 境明神 万延元年(1860)
http://www.wasan.jp/fukusima/sakai1L2.html
団扇の中に小円 1 個と長方形が内接し,長方形の中に大円 2 個,小円 7 個が入っている。
小円の径を 1 としたとき,団扇の径はいかほどか。
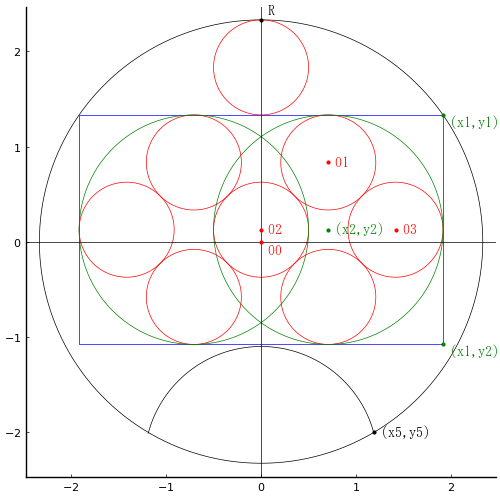
長方形内の小円の入り方で長方形の長辺,短辺の長さおよび小円の中心座標は簡単に計算できる。
小円の半径を r,外円の半径と中心座標を R, (0, 0),長方形の右上の頂点座標を (x1, y1) とする。
(x1, y1) は外円の円周上にあるので,等円の半径,外円の半径を r, R として以下の方程式をとき R = r*(4*sqrt(2) + 13)/4 を得る。
include("julia-source.txt")
using SymPy
@syms r::positive, R::positive, x5::positive, y5::negative
x1 = 2√Sym(2)r + r
y1 = R - 2r
eq = x1^2 + y1^2 - R^2
R = solve(eq, R)[1]
R |> println
r*(4*sqrt(2) + 13)/4
r = 1/2 のとき,R = 2.3321067811865475 で,直径は 4.664213562373095 となる。答えでは 団扇の著系は 5 寸 となっているので,一致しない。
r = 1/2
R = r*(4*sqrt(2) + 13)/4
R, 2R
(2.3321067811865475, 4.664213562373095)
以上で団扇の主要部を描くことができるが追加で,団扇の下部の竹の骨が見えている円弧部分の描画に必要な座標 (x5, y5) を計算する。
@syms r::positive, R::positive, x5::positive, y5::negative
y2 = R - 3r - √Sym(2)r
eq2 = x5^2 + (R + y5)^2 - (R + y2)^2/4
eq3 = x5^2 + y5^2 - R^2
solve([eq2, eq3], (x5, y5))
1-element Vector{Tuple{Sym, Sym}}:
(sqrt(3*R^4/4 - 3*R^3*r/2 - sqrt(2)*R^3*r/2 - 11*R^2*r^2/8 - 3*sqrt(2)*R^2*r^2/4 + 29*sqrt(2)*R*r^3/8 + 45*R*r^3/8 - 193*r^4/64 - 33*sqrt(2)*r^4/16)/R, (-4*R^2 - 12*R*r - 4*sqrt(2)*R*r + 6*sqrt(2)*r^2 + 11*r^2)/(8*R))
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1/2
R = r*(4*sqrt(2) + 13)/4 # R は後々の制約条件から決まる
println("R = $R, $(1 + sqrt(2))")
println("2R = $(2R), $(2(1 + sqrt(2)))")
a = 1 + sqrt(2)
x1 = 2√2r + r
y1 = R - 2r
# (x1, y1) が外円の円周上にあるには x1^2 + y1^2 = R^2 でなければならない。
y2 = R - 3r - √2r
x2 = x1 - r - √2r
y3 = y1 - 2a*r
plot([x1, -x1, -x1, x1, x1], [y1, y1, y3, y3, y1], color=:blue, lw=0.5)
circle(0, 0, R, :black)
circle(0, R - r, r)
circle(x2, y2 + √2r, r)
circle(x2, y2 - √2r, r)
circle(x2 - √2r, y2, r)
circle(x2 + √2r, y2, r)
circle(x2, y2, (√2 + 1)r, :green)
circle(-x2, y2 + √2r, r)
circle(-x2, y2 - √2r, r)
circle(-x2 - √2r, y2, r)
circle(-x2, y2, ( √2 + 1)r, :green)
(x5, y5) = (sqrt(3*R^4/4 - 3*R^3*r/2 - sqrt(2)*R^3*r/2 - 11*R^2*r^2/8 - 3*sqrt(2)*R^2*r^2/4 + 29*sqrt(2)*R*r^3/8 + 45*R*r^3/8 - 193*r^4/64 - 33*sqrt(2)*r^4/16)/R, (-4*R^2 - 12*R*r - 4*sqrt(2)*R*r + 6*sqrt(2)*r^2 + 11*r^2)/(8*R))
θ = atand(y5+R, x5)
println(θ)
circle(0, -R, (R + y2)/2, :black, beginangle=θ, endangle=181-θ)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(x1, y1, " (x1,y1)")
point(x1, y2 - (√2 + 1)r, " (x1,y2)")
point(x2, y2, " (x2,y2)", :green, :left, :vcenter)
point(0, 0, " O0", :red, :left, delta=-delta/2)
point(x2, y2 + √2r, " O1", :red, :left, :vcenter)
point(0, y2, " O2", :red, :left, :vcenter)
point(x2 + √2r, y2, " O3", :red, :left, :vcenter)
point(0, R, " R", :black, :left, :bottom, delta=delta/2)
point(x5, y5, " (x5,y5)", :black, :left, :vcenter)
end
end;



















