算額（その652）

算額（その652）

群馬県吾妻郡東吾妻町 一宮神社 明治5年(1872)3月
http://www.wasan.jp/gunma/itinomiya.html

この算額の問・答・術はほとんど判読できない。図はかろうじて見ることができるので，以下のようなものでもあろうかと推測して問を建ててみた。

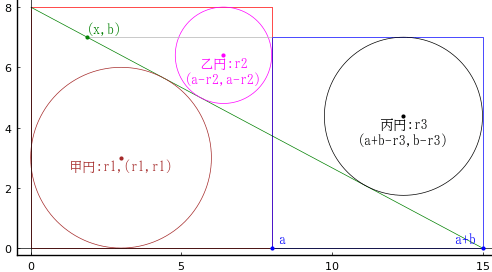
正三角形と甲円，乙円，丙円がある。甲円，乙円はそれぞれ正三角形の斜辺に 2 点で接しており，甲円と乙円は外接している。丙円は甲円と正三角形の底辺が作る弧の中にあり，底辺と甲円に接している。
正三角形の一辺の長さと甲円の直径がわかっているときに，乙円の直径を求めよ。

正三角形の一辺の長さを 2a とする。
甲円の半径と中心座標を r1, (0, y1)
乙円の半径と中心座標を r2, (0, y1 )
丙円の半径と中心座標を r3, (0, y1)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, r1::positive, y1::positive, r2::positive, r3::positive
eq1 = (y1 - r1) + 2r3
eq2 = dist(0, sqrt(Sym(3))a, a, 0, 0, y1) - r1^2
eq3 = r2/(sqrt(Sym(3))a - y1 - r1 - r2) - 1//2
res = solve([eq1, eq2, eq3], (y1, r2, r3))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (sqrt(3)*a - 2*r1, r1/3, -sqrt(3)*a/2 + 3*r1/2)

乙円は甲円の 1/3 の大きさである。
甲円の直径が 150 のとき，乙円の直径は 50 である。

その他のパラメータは以下の通り。

a = 100;  r1 = 75;  y1 = 23.2051;  r2 = 25;  r3 = 25.8975

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 100
   r1 = 75
   (y1, r2, r3) = (√3a - 2r1, r1/3, (3r1 - √3a)/2)
   @printf("a = %g;  r1 = %g;  y1 = %g;  r2 = %g;  r3 = %g\n", a, r1, y1, r2, r3)
   plot([a, 0, -a, a], [0, √3a, 0, 0], color=:black, lw=0.5)
   circle(0, y1, r1)
   circle(0, -r3, r3, :blue)
   circle(0, r2 + r1 + y1, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, y1, " 甲円:r1,(0, y1)", :red, :left, :vcenter)
       point(0, y1 + r1 + r2, " 乙円:r2,(0,y1+r1+r2)", :green, :left, :vcenter)
       point(0, -r3, " 丙円:r3,(0,-r3)", :blue, :left, :vcenter)
       point(0, √3a, " √3a", :black, :left, :vcenter)
       point(a, 0, "a", :black, :left, :bottom, delta=delta/2)
   end
end;

算額（その651）

算額（その651）

長野県飯山市静間大久保 静間観音堂（静観庵）弘化5年(1848)

中村信弥「改訂増補 長野県の算額」県内の算額（177）
http://www.wasan.jp/zoho/zoho.html

日堂薫，宮崎雄也，鷲森勇希，伊藤栄一：「飯山市静間観音堂の算額」の復元
https://sbc21.co.jp/gakkokagaku/2015/27.pdf

直径と2本の弦を隔てて 4 個の等円が外円に内接し，直径と弦に接している。等円の直径を外円の直径で表わせ。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R, r, x, y1, x0, y2
y0 = sqrt(R^2 - x0^2)
eq1 = x^2 + y2^2 - (R - r)^2
eq2 = r^2 + y1^2 - (R - r)^2
eq3 = dist(0, R, x0, -y0, r, y1) - r^2
eq4 = dist(0, R, x0, -y0, x, y2) - r^2
eq5 = y2/x * (y0 + R)/x0 - 1;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r, x, y1, x0, y2) = u
   t = -R - sqrt(R^2 - x0^2)
   t2 = x0^2 + t^2
   return [
       x^2 + y2^2 - (R - r)^2,  # eq1
       r^2 + y1^2 - (R - r)^2,  # eq2
       -r^2 + (r - x0*(r*x0 + (-R + y1)*t)/t2)^2 + (-R + y1 - t*(r*x0 + (-R + y1)*t)/t2)^2,  # eq3
       -r^2 + (x - x0*(x*x0 + (-R + y2)*t)/t2)^2 + (-R + y2 - t*(x*x0 + (-R + y2)*t)/t2)^2,  # eq4
       -1 + y2*(R + sqrt(R^2 - x0^2))/(x*x0),  # eq5
   ]
end;
R = 1
iniv = BigFloat[8, 17, -18, 18, 8] ./26
iniv = BigFloat[0.313, 0.637, -0.612, 0.694, 0.257] .* R
res = nls(H, ini=iniv)

   (BigFloat[0.3129063194259740325268103642250497724124515879919851568449522877018154669364085, 0.6371784719628400853411527943465112615089968502655608047796456430352258943786332, -0.6117085589952554644133700611927907136554589335804161767166315804026984221703721, 0.6940076375173001867788131238285698449294652216735132602273056924441179784109038, 0.2571017711954972908126786596219933186205074882118679191481568858007998140638422], true)

等円の直径は外円の直径の 0.312906 倍である。

   r = 0.3129063194259740325268103642250497724124515879919851568449522877018154669364085
   R = 1;  r = 0.312906;  x = 0.637178;  y1 = -0.611709;  y2 = 0.257102;  x0 = 0.694008

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r, x, y1, x0, y2) = res[1]
   println("r = $r")
   @printf("R = %g;  r = %g;  x = %g;  y1 = %g;  y2 = %g;  x0 = %g\n", R, r, x, y1, y2, x0)
   y0 = -sqrt(R^2 - x0^2) 
   plot([x0, 0, -x0], [y0, R, y0], color=:black, lw=0.5)
   circle(0, 0, R)
   circle(x, y2, r, :blue)
   circle(-x, y2, r, :blue)
   circle(r, y1, r, :blue)
   circle(-r, y1, r, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x, y2, "(x,y2)")
       point(r, y1, "(r,y1)")
       point(x0, y0, " (x0,y0)", :red)
       point(R, 0, "R ", :red, :right, :bottom, delta=delta/2)
   end
end;

『「飯山市静間観音堂の算額」の復元』には，記号を上に合わせると，r について以下の 3 次式が示されている。
R = 1 にして方程式を解くと，実数解 1 つが得られ，
-(1133/8 + 15*sqrt(114))^(1/3)/3 + 71/(12*(1133/8 + 15*sqrt(114))^(1/3)) + 5/3
評価すると上と同じく r = 0.312906319425974 が得られる。

@syms R, r
eq = 4r^3 - 20R*r^2 + 57R^2*r - 16R^3;

res2 = solve(eq(R=>1));
res2[3] |> println

   -(1133/8 + 15*sqrt(114))^(1/3)/3 + 71/(12*(1133/8 + 15*sqrt(114))^(1/3)) + 5/3

res2[3].evalf() |> println

   0.312906319425974

 

算額（その650）

算額（その650）

神壁算法 東都麹町 橘田彌曾八元克 天明九年
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

全円内に 2 本の弦と 2 個の等円が入っている。全円，等円の直径がそれぞれ 697寸，272寸のとき水平の弦の長さはいかほどか。

全円の半径と中心座標を R, (0, 0)
等円の半径と中心座標を r, (x1, y1), (x2, y + r)
水平な弦と y 軸の交点座標を (0, y)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R, r, x1, y1, x2::negative, x::negative, y::negative
eq1 = x1^2 + y1^2 - (R - r)^2
eq2 = x2^2 + (y + r)^2 - (R - r)^2
eq3 = y1/x1 * (sqrt(R^2 - x^2) - y)/(x -sqrt(R^2 - y^2)) + 1
eq4 = distance(x, sqrt(R^2- x^2), sqrt(R^2 - y^2), y, x1, y1) - r^2
eq5 = distance(x, sqrt(R^2- x^2), sqrt(R^2 - y^2), y, x2, y + r) - r^2;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (x1, y1, x2, x, y) = u
   dy = sqrt(R^2 - x^2)
   dx = sqrt(R^2 - y^2)
   return [
       x1^2 + y1^2 - (R - r)^2,  # eq1
       x2^2 - (R - r)^2 + (r + y)^2,  # eq2
       1 + y1*(dy - y)/(x1*(-dx + x)),  # eq3
       -r^2 + (x1 - (x1*(dx^2 - 2*dx*x + dy^2 - 2*dy*y + x^2 + y^2) + (dy - y)*(dx*dy - dx*y1 - dy*x1 - x*y + x*y1 + x1*y))/(dx^2 - 2*dx*x + dy^2 - 2*dy*y + x^2 + y^2))^2 + (y1 - (y1*(dx^2 - 2*dx*x + dy^2 - 2*dy*y + x^2 + y^2) + (dx - x)*(dx*dy - dx*y1 - dy*x1 - x*y + x*y1 + x1*y))/(dx^2 - 2*dx*x + dy^2 - 2*dy*y + x^2 + y^2))^2,  # eq4
       -r^2 + (x2 - (x2*(dx^2 - 2*dx*x + dy^2 - 2*dy*y + x^2 + y^2) + (dy - y)*(dx*dy - dx*r - dx*y - dy*x2 + r*x + x2*y))/(dx^2 - 2*dx*x + dy^2 - 2*dy*y + x^2 + y^2))^2 + (r + y - ((dx - x)*(dx*dy - dx*r - dx*y - dy*x2 + r*x + x2*y) + (r + y)*(dx^2 - 2*dx*x + dy^2 - 2*dy*y + x^2 + y^2))/(dx^2 - 2*dx*x + dy^2 - 2*dy*y + x^2 + y^2))^2,  # eq5
   ]
end;

(R, r) = (697, 272) .// 2
iniv = BigFloat[110, 180, -200, -250, -90]
res = nls(H, ini=iniv)

   (BigFloat[99.9999999999999999999999999999999999999999999999999999999999999999999970530364, 187.5000000000000000000000000000000000000000000000000000000000000000000016344705, -208.0000000000000000000000000000000000000000000000000000000000000000000319742255, -264.0000000000000000000000000000000000000000000000000000000000000000000687439946, -92.5000000000000000000000000000000000000000000000000000000000000000000529196718], true)

水平な弦の長さは 672 寸である。

その他のパラメータは以下の通り。
x1 = 100;  y1 = 187.5;  x2 = -208;  x = -264;  y = -92.5

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r) = (697, 272) .// 2
   (x1, y1, x2, x, y) = res[1]
   弦 = 2sqrt(R^2 - y^2)
   @printf("弦 = %g;  x1 = %g;  y1 = %g;  x2 = %g;  x = %g;  y = %g\n",
       弦, x1, y1, x2, x, y)
   plot()
   circle(0, 0, R, :magenta)
   circle(x1, y1, r)
   circle(x2, y + r, r)
   segment(x, sqrt(R^2 - x^2), sqrt(R^2 - y^2), y, :green)
   segment(-sqrt(R^2 - y^2), y, sqrt(R^2 - y^2), y, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(R, 0, " R", :magenta, :left, :bottom, delta=delta/2)
       point(x1, y1, " 等円:r\n (x1,y1)", :red, :left, :vcenter)
       point(x2, y + r, " (x2,y+r)", :red, :left, :vcenter)
       point(0, y, " y", :blue, :left, delta=-delta/2)
       point(x, sqrt(R^2-x^2), " (x,sqrt(R^2-x^2)", :green, :left, :bottom, delta=-delta/2)
       point(sqrt(R^2-y^2), y, "(sqrt(R^2-y^2),y) ", :blue, :right, :top, delta=-delta/2)
   end
end;

算額（その649）

算額（その649）

神壁算法 筑後州久留米 城崎庄右衛門方弘 天明八年
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

大円内に互いに外接する小円が入っている。それぞれの小円は大円に内接している。小円の直径と，小円に囲まれた中央部の面積（黒積と呼ぶ）が与えられたとき，小円の個数を求めよ。

小円の個数を n，大円と小円の半径を R, r とする。
黒積を bとして，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms b, R, r, n
eq1 = sin(PI/n) - r/(R-r)
eq2 = 2n*(sqrt((R - r)^2 - r^2)*r/2 - PI*r^2*(90 - 360/2n)/360) - b |> simplify
res = solve([eq1, eq2], (b, R))

   1-element Vector{Tuple{Sym, Sym}}:
    (r*(-pi*n*r + 2*n*sqrt(r^2/tan(pi/n)^2) + 2*pi*r)/2, r + r/sin(pi/n))

小円の個数と直径と黒積の関係を表す関数は以下のようなものになる。
この式を n について解くことができれば，解はすぐに求まるが，SymPy では解けないので，n, r について黒積を計算し，適切な n を知ることはできる。

fb(r, n) = r*(-pi*n*r + 2*n*sqrt(r^2/tan(pi/n)^2) + 2*pi*r)/2;

たとえば，小円の直径が 3 で，与えられた黒積が約 123.6 のとき，小円の個数 n が特定の値をとるときの黒積のリストを計算すると以下のようになる。
小円の個数は 9 個であると推定される。

for n in 6:12
   println("n = $n;  黒積 = $(fb(3, n))")
end

   n = 6;  黒積 = 36.9820758441031
   n = 7;  黒積 = 60.13501327828686
   n = 8;  黒積 = 89.00037484393842
   n = 9;  黒積 = 123.58550238774589
   n = 10;  黒積 = 163.8941828165403
   n = 11;  黒積 = 209.92853417964912
   n = 12;  黒積 = 261.68981780589803

fb(3, 7)

   60.13501327828686

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   n = 7
   r = 3
   R = r + r/sin(pi/n)
   黒積 = r*(-pi*n*r + 2*n*sqrt(r^2/tan(pi/n)^2) + 2*pi*r)/2
   @printf("小円の直径 = %g;  黒積 = %g;  n = %g; R = %g\n", 2r, 黒積, n, R)
   plot()
   circle(0, 0, R)
   circlef(0, 0, (R - r)cosd(180/n), :black)
   rotatef(0, R - r, r, :white, angle=360/n)
   rotate(0, R - r, r, :blue, angle=360/n)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       # vline!([0], color=:black, lw=0.5)
       # hline!([0], color=:black, lw=0.5)
   end
end;

算額（その648）

算額（その648）

岐阜県不破郡垂井町宮代 南宮大社奉納算額 天保13年
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF

楕円の中に大，中，小の正方形を入れる。大正方形の一辺の長さが与えられたとき，小正方形の一辺の長さを求めよ。

楕円の長径，短径を a, b
大正方形の一辺の長さを '大'
小正方形の一辺の長さを '小'
中正方形の楕円の周上の座標を (b + y1, y1)
小正方形の楕円の周上の座標を (b, y2)
とおき，以下の連立方程式を解く。
eq5 は'大'を求めてから単純に計算するだけであるが，面倒くさいので入れておく。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms 大::positive, 小::positive, a::positive, b::positive, y1::positive, y2::positive

eq1 = b + 2y1 - a
eq2 = b^2/a^2 + y2^2/b^2 - 1
eq3 = (b + y1)^2/a^2 + y1^2/b^2 - 1
eq4 = b - 大/sqrt(Sym(2))
eq5 = y2/sqrt(Sym(2)) - 小;
res = solve([eq1, eq2, eq3, eq4, eq5], (小, a, b, y1, y2))

   1-element Vector{NTuple{5, Sym}}:
    (大*sqrt(-2 + 2*sqrt(2))/2, 大*(sqrt(2) + 2)/2, sqrt(2)*大/2, 大/2, 大*sqrt(-1 + sqrt(2)))

小正方形の一辺の長さは，大正方形の一辺の長さの √(2√2 - 2)/2 倍である。
大正方形の一辺の長さを 1 とすると，小正方形の一辺の長さは 0.455089860562227 である。

その他のパラメータは以下の通り。

a = 1.70711;  b = 0.707107;  y1 = 0.5; y2 = 0.643594

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   大 = 1
   (小, a, b, y1, y2) = (大*sqrt(-2 + 2*sqrt(2))/2, 大*(sqrt(2) + 2)/2, sqrt(2)*大/2, 大/2, 大*sqrt(-1 + sqrt(2)))
   @printf("小正方形の一辺の長さ = %g;  a = %g;  b = %g;  y1 = %g; y2 = %g\n",
      小, a, b, y1, y2)
   plot([a, b + y1, 0, -b - y1, -a, -b - y1, 0, b + y1, a],
       [0, y1, -b, y1, 0, -y1, b, -y1, 0], color=:red, lw=0.5)
   x = [b - y2/2, b, b + y2/2]
   y = [y2/2, y2, y2/2]
   plot!(x, y, color=:red, lw=0.5)
   plot!(x, -y, color=:red, lw=0.5)
   plot!(-x, y, color=:red, lw=0.5)
   plot!(-x, -y, color=:red, lw=0.5)
   ellipse(0, 0, a, b, color=:blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, b, " b", :blue, :left, :bottom, delta=delta/2)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(b, y2, "(b, y2)", :red, :left, :bottom, delta=delta/2)
       point(b + y1, y1, "(b+y1,y1)", :red, :left, :bottom, delta=delta/2)
   end
end;

算額（その647）

算額（その647）

長野県長和町 駒形神社 明治8年(1875)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

5 個の等円が隣の等円と外接し円弧に外接している。両端の等円は弦の延長線に接している。
矢が 8 寸，弦が 24 寸のとき，等円の直径を求めよ。

円弧が一部である円の半径と中心座標を R, (0, 0)
等円の半径と中心座標を r, (0, R + r), (x1, y1), (x2, y + r)
弦と y 軸の交点座標を (0, y)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r::positive, y::positive,
     x1::positive, y1::positive, x2::positive, y2::positive

eq1 = x1^2 + y1^2 - (R + r)^2
eq2 = x2^2 + (y + r)^2 - (R + r)^2
eq3 = x1^2 + (R + r - y1)^2 - 4r^2
eq4 = (x2 - x1)^2 + (y1 - y - r)^2 - 4r^2
eq5 = y - sqrt(R^2 - 12^2)
eq6 = y - (R - 8)

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (R, r, y, x1, y1, x2) = u
   return [
       x1^2 + y1^2 - (R + r)^2,  # eq1
       x2^2 - (R + r)^2 + (r + y)^2,  # eq2
       -4*r^2 + x1^2 + (R + r - y1)^2,  # eq3
       -4*r^2 + (-x1 + x2)^2 + (-r - y + y1)^2,  # eq4
       y - sqrt(R^2 - 144),  # eq5
       -R + y + 8,  # eq6
   ]
end;
g = 12
iniv = BigFloat[13, 4.3, 5, 8.3, 15, 14.6]
res = nls(H, ini=iniv)

   (BigFloat[13.0, 4.292842863236655796258424878247800048144346796834551378448796255304952228172366, 5.0, 8.316932815223808406463820238890995876085407092697237813856266028198192952429316, 15.16149870031483123032399683773288234968648696208586379659490076589161640834934, 14.58374046024498108560260206110599459102827635604655955326101083845210751031903], true)

等円の直径は約 8.58569 となるが，中村も指摘しているように，題意が不明瞭であることと，原問題の条件と答えに合う図にならない。

その他のパラメータは以下の通り。
R = 13;  r = 4.29284; y = 5;  x1 = 8.31693;  y1 = 15.1615;  x2 = 14.5837

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r, y, x1, y1, x2) = res[1]
   @printf("等円の直径 = %g;  R = %g;  r = %g; y = %g;  x1 = %g;  y1 = %g;  x2 = %g\n",
       2r, R, r, y, x1, y1, x2)
   plot()
   circle(0, 0, R, :blue, beginangle=0, endangle=180)
   circle(0, R + r, r, :red)
   circle(x1, y1, r, :red)
   circle(-x1, y1, r, :red)
   circle(x2, y + r, r, :red)
   circle(-x2, y + r, r, :red)
   hline!([y], color=:gray80)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, y, " y", :black, :left, delta=-delta/2)
       point(0, R, " R", :blue, :left, delta=-delta/2)
       point(0, R + r, " R+r", :red, :left, :vcenter)
       point(x1, y1, "(x1,y1)", :red, :center, delta=-delta/2)
       point(x2, y + r, "(x2,y+r)", :red, :center, delta=-delta/2)
   end
end;

算額（その646）

算額（その646）

長野県東御市 大日如来堂（長命寺） 嘉永6年(1853)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

二等辺三角形に初円は底辺と斜辺に接している。順次，第n円は (n - 1) 円と斜辺に接している。
二等辺三角形の高さを h，底辺の長さを 2a，斜辺の長さを b とする。

初円の半径と中心座標を r1, (0, r1)
二円の半径と中心座標を r2, (0, 2r1 + r2)
とおき，以下の連立方程式を解き r1, r2 を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, b::positive, h::positive, r1::positive, r2::positive, b1::positive, b2::positive

h = sqrt(b^2 - a^2)
sinθ = a/sqrt(a^2 + h^2)
eq1 = r1/(h - r1) - sinθ
eq2 = r2/(h - 2r1 - r2) - sinθ;
res = solve([eq1, eq2], (r1, r2))

   Dict{Any, Any} with 2 entries:
     r2 => a*(-a + b)*sqrt(-a^2 + b^2)/(a^2 + 2*a*b + b^2)
     r1 => a*sqrt(-a^2 + b^2)/(a + b)

r1 = a*sqrt(-a^2 + b^2)/(a + b)
r2 = a*(-a + b)*sqrt(-a^2 + b^2)/(a^2 + 2*a*b + b^2);

これらの円は互いに相似なので，半径は初項が r1，公比が r2/r1 の等比数列になる。
n 番目の円（最終の円）の半径は以下の式で表される。

@syms n
eq11 = r1*(r2/r1)^(n - 1) |> simplify
eq11 |> println

   a*(a + b)*(-a^2 + b^2)^(n - 1/2)/(a^2 + 2*a*b + b^2)^n

この半径が最大になるときの底辺の長さは，eq11 を a で偏微分し，導関数が　0 になるときの a を求めればよい。

eq12 = diff(eq11, a) |> simplify
eq12 |> println

   (-a^2 + b^2)^(n - 1/2)*(a^2 + 2*a*b*n - a*b - b^2)/((a - b)*(a^2 + 2*a*b + b^2)^n)

SymPy は「この式 = 0」をそのまま解くことができない。

式の項を検討すると，a^2 + 2*a*b*n - a*b - b^2 = 0 を解けばよいことがわかる。
式を直接書いてもよいが，args で取り出す。

eq12.args

   (1/(a - b), (-a^2 + b^2)^(n - 1/2), (a^2 + 2*a*b + b^2)^(-n), a^2 + 2*a*b*n - a*b - b^2)

eq12.args[4] |> println

   a^2 + 2*a*b*n - a*b - b^2

res = solve(eq12.args[4], a)
res |> println

   Sym[b*(-2*n - sqrt(4*n^2 - 4*n + 5) + 1)/2, b*(-2*n + sqrt(4*n^2 - 4*n + 5) + 1)/2]

2 番目のものが適解である。

底辺の長さは b*(-2*n + sqrt(4*n^2 - 4*n + 5) + 1) である。

2res[2] |> println

   b*(-2*n + sqrt(4*n^2 - 4*n + 5) + 1)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (n, b) = (4, 15)
   println("n = $n;  b = $b")
   a = b*(sqrt(4n^2 - 4n + 5) - 2n + 1)
   println("a = $a")
   h = sqrt(b^2 - a^2)
   println("h = $h")
   r1 = a*sqrt(-a^2 + b^2)/(a + b)
   r2 = a*(-a + b)*sqrt(-a^2 + b^2)/(a^2 + 2*a*b + b^2)
   plot([a, 0, -a, a], [0, h, 0, 0], color=:gray80, lw=0.5)
   circle(0, r1, r1, :blue)
   circle(0, 2r1 + r2, r2, :red)
   r = zeros(n)
   r[1] = r1
   r[2] = r2
   y = zeros(n)
   for i = 3:n
       r[i] = r1*(r2/r1)^(i - 1)
       y[i] = 2sum(r[1:i]) - r[i]
       circle(0, y[i], r[i], i)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, r1, " (0,r1)", :blue, :left, :vcenter)
       point(0, 2r1 + r2, " (0,2r1+r2)", :red, :left, :vcenter)
       point(0, y[3], " (0,2r1+2r2+r3)", :green, :left, :vcenter)
       point(0, y[4], " (0,2r1+2r2+2r3+r4)", :purple, :left, :vcenter)
   end
end;

 

算額（その645）

算額（その645）

長野県小諸市八幡町 八幡神社 寛政11年(1799)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

鈎股弦（直角三角形）内に内接円があり，中鈎（直角の頂点から斜辺（弦）への垂線）を引く。短弦と円の直径の積が 3.6 平方寸，中鈎と円の直径の積が 4.8 平方寸のとき，円の直径を求めよ。

直角三角形の 3 辺を鈎，股，弦，弦 = 短弦 + 長弦，中鉤と弦の交点座標を (x, y)，円の直径を円径として以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
     中鈎::positive, 短弦::positive, 長弦::positive,
     円径::positive, x::positive, y ::positive

eq1 = 短弦^2 + 中鈎^2 - 鈎^2
eq2 = 短弦 * 円径 - 3.6
eq3 = 中鈎 * 円径 - 4.8
eq4 = 鈎 + 股 - 弦 - 円径
eq5 = 鈎^2 + 股^2 - 弦^2
eq6 = 長弦^2 + 中鈎^2 - 股^2
eq7 = 長弦 + 短弦 - 弦
eq8 = (x^2 + y^2) + (x^2 + (鈎 - y)^2) - 鈎^2
eq9 = (x^2 + y^2) + ((股 - x)^2 + y^2) - 股^2
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (円径, 鈎, 股, 弦, 中鈎, 短弦, 長弦, x, y))

   1-element Vector{NTuple{9, Sym}}:
    (2.00000000000000, 3.00000000000000, 4.00000000000000, 5.00000000000000, 2.40000000000000, 1.80000000000000, 3.20000000000000, 1.44000000000000, 1.92000000000000)

円の直径は 2 寸である。

その他のパラメータは以下の通りである。

鈎 = 3;  股 = 4;  弦 = 5;  中鈎 = 2.4;  短弦 = 1.8;  長弦 = 3.2;  x = 1.44;  y = 1.92

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (円径, 鈎, 股, 弦, 中鈎, 短弦, 長弦, x, y) = res[1]
   @printf("円径 = %g;  鈎 = %g;  股 = %g;  弦 = %g;  中鈎 = %g;  短弦 = %g;  長弦 = %g;  x = %g;  y = %g\n",
       円径, 鈎, 股, 弦, 中鈎, 短弦, 長弦, x, y)
   r = 円径/2
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:black, lw=0.5)
   circle(r, r, r, :blue)
   segment(0, 0, x, y, :red)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x, y, " (x,y)", :red, :left, :vcenter)
       point(0, 鈎, " 鈎", :black, :left, :vcenter)
       point(股, 0, "股", :black, :left, :bottom, delta=delta/2)
       point(r, r, " (r,r)", :blue, :left, :vcenter)
       point(0.6, 2.7, "短弦", mark=false)
       point(2.8, 1.05, "長弦", mark=false)
       point(0.75, 1.5, "中鈎", mark=false)
   end
end;

算額（その644）

算額（その644）

長野県軽井沢町峠 熊野神社 安政4年(1857)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

二等辺三角形の中に大円，中円，荘園が入っている。中円は大円と等辺の接点を結ぶ直線に接している。また，小円は沖苑に内接し，大円に外接している。小円の直径が 1 寸のとき，中円の直径を求めよ。

二等辺三角形の底辺の長さを 2a，高さを h とする。また，大円と等辺の接点座標を (c, h) とする。
大円の半径と中心座標を r1, (0, r1)
中円の半径と中心座標を r2, (0, b + r2)
小円の半径と中心座標を r3, (0, 2r1 + r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r1::positive, r2::positive, r3::positive, a::positive, b::positive, c::positive, h::positive

r3 = 1//2
eq1 = r1/(h - r1) - a/sqrt(a^2 + h^2)
eq2 = r2/(h - b - r2) - a/sqrt(a^2 + h^2)
eq3 = c/(h - b) - a/h
eq4 = r2/r1 - a/h
eq5 = b^2 + (a - c)^2 - a^2
eq6 = b + 2r2 - (2r1 + 2r3)using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r1, r2, a, b, c, h) = u
   return [
       -a/sqrt(a^2 + h^2) + r1/(h - r1),  # eq1
       -a/sqrt(a^2 + h^2) + r2/(-b + h - r2),  # eq2
       -a/h + c/(-b + h),  # eq3
       -a/h + r2/r1,  # eq4
       -a^2 + b^2 + (a - c)^2,  # eq5
       b - 2*r1 + 2*r2 - 1,  # eq6
   ]
end;

iniv = BigFloat[1.67, 1.1, 2.42, 2.14, 2.2, 6.43]
res = nls(H, ini=iniv)

   (BigFloat[1.883203505913525864168947465362055090560951328672239179557958847642330007152124, 0.9999999999999999999999999999999999999999999999999999999915012754481286025568294, 3.132241882311900195655072338157300657084786186095832984118051754533183394146556, 2.766407011827051728337894930724110181121902657344478359132915144388402809190606, 1.663251938771469380287813597004943645093506732800541877736976628888590678029407, 5.898648894138951923992967268881410838206688843440311343250654955537926982258505], true)

中円の半径は 1寸（直径は 2 寸）である。
その他のパラメータは以下の通り。
r1 = 1.8832;  r2 = 1;  a = 3.13224;  b = 2.76641;  c = 1.66325;  h = 5.89865

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1//2
   (r1, r2, a, b, c, h) = res[1]
   @printf("r1 = %g;  r2 = %g;  a = %g;  b = %g;  c = %g;  h = %g\n", r1, r2, a, b, c, h)
   plot([a, 0, -a, a], [0, h, 0, 0], color=:black, lw=0.5)
   circle(0, r1, r1, :blue)
   circle(0, b + r2, r2)
   circle(0, 2r1 + r3, r3, :green)
   segment(c, b, -c, b)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(c, b, " (c,b)", :black, :left, :vcenter)
       point(0, r1, " 大円:r1,(0, r1)", :blue, :left, :vcenter)
       point(0, b + r2, " 中円:r2\n (0,b+r2)", :red, delta=-2delta)
       point(0, 2r1 + r3, " 小円:r3\n (0,2r1+r3)", :black, :left, :vcenter)
       point(0, h, " h", :black, :left, :vcenter)
       point(a, 0, " a", :black, :left, :bottom, delta=delta/2)
   end
end;

算額（その643）

算額（その643）

長野県軽井沢町峠 熊野神社 安政4年(1857)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

外円の中に 4 つの円弧と 2 つの等円が入っている。等円は互いに外接し円弧とも外接している。
大矢，小矢がそれぞれ 49寸，36.75寸のとき，等円の直径を求めよ。

外円の半径と中心座標を r0, (0, 0)
等円の半径と中心座標を r1, (r1, y1)
上部の円弧を構成する円の半径と中心座標を r2, (r2, r0)
下部の円弧を構成する円の半径と中心座標を r3, (r3, -r0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r0::positive, r1::positive, y1::positive, r2::positive, r3::positive

eq1 = (r2 - r1)^2 + (r0 - y1)^2 - (r1 + r2)^2
eq2 = r2^2 + r0^2 - (r0 + r2 - 3675//100)^2
eq3 = r3^2 + r0^2 - (r0 + r3 - 49)^2
eq4 = r0 - sqrt(r2*r3)
eq5 = 1/sqrt(r2) + 1/sqrt(r3) - 1/sqrt(r1);

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r0, r1, y1, r2, r3) = u
   return [
       (r0 - y1)^2 + (-r1 + r2)^2 - (r1 + r2)^2,  # eq1
       r0^2 + r2^2 - (r0 + r2 - 147/4)^2,  # eq2
       r0^2 + r3^2 - (r0 + r3 - 49)^2,  # eq3
       r0 - sqrt(r2)*sqrt(r3),  # eq4
       1/sqrt(r3) + 1/sqrt(r2) - 1/sqrt(r1),  # eq5
   ]
end;

iniv = BigFloat[73.5, 20, 10, 54, 97]
res = nls(H, ini=iniv)

   (BigFloat[73.49999999999999999999999999999999999999999999999999999999999999999999999999889, 17.99999999999999999999999999999999999999999999999999999999999999999999511910947, 10.50000000000000000000000000000000000000000000000000000000000000000000678816348, 55.12500000000000000000000000000000000000000000000000000000000000000000000000055, 97.99999999999999999999999999999999999999999999999999999999999999999999999999779], true)

等円の半径は 18 寸である（直径 36寸 ）。
その他のパラメータは以下の通りである。

r0 = 73.5;  r1 = 18;  y1 = 10.5;  r2 = 55.125;  r3 = 98

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, r1, y1, r2, r3) = res[1]
   @printf("r0 = %g;  r1 = %g;  y1 = %g;  r2 = %g;  r3 = %g\n", r0, r1, y1, r2, r3)
   plot()
   circle(0, 0, r0, :blue)
   circle(r1, y1, r1)
   circle(-r1, y1, r1)
   circle(r2, r0, r2, :green)
   circle(-r2, r0, r2, :green)
   circle(r3, -r0, r3, :magenta)
   circle(-r3, -r0, r3, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(r1, y1, "(r1,y1)",)
       point(r2, r0, "(r2,r0)")
       point(r3, -r0, "(r3,-r0) ", :magenta, :right, :bottom, delta=delta/2)
       point(r0, 0, " r0", :blue, :left, :bottom, delta=delta/2)
       fr3 = Float64(r3)
       fr0 = Float64(r0)
       rect(-fr3, -fr0, fr3, fr0)
       plot!(xlims=(-fr3 - 5, fr3 + 5), ylims=(-fr0 - 5, fr0 + 5))
       θ = atand(r0/r2)
       (px1, py1, px2, py2) = (r0*cosd(θ), r0*sind(θ), 2(r0 - r2)*cosd(θ), 2(r0 - r2)*sind(θ))
       segment(0, 0, r2, r0, :gray60)
       segment(px1, py1, px2, py2, lw=1)
       segment(-px1, py1, -px2, py2, lw=1)
       point((px1 + px2)/2, (py1 + py2)/2, " 小矢", mark=false)
       θ = atand(-r0/r3)
       (px1, py1, px2, py2) = (r0*cosd(θ), r0*sind(θ), -(r0 - r3)*cosd(θ), -(r0 - r3)*sind(θ))
       segment(0, 0, r3, -r0, :gray60)
       segment(px1, py1, px2, py2, lw=1)
       segment(-px1, py1, -px2, py2, lw=1)
       point((px1 + px2)/2, (py1 + py2)/2, " 大矢", mark=false, delta=2delta)
   end
end;

算額（その642）

算額（その642）

長野県飯田市八幡町 松尾八幡神社（鳩ヶ嶺八幡宮） 明治6年(1873)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

外円に二等辺三角形が内接し，金円，銀円が入っている。
外円の直径が 10 寸のとき，金円，銀円の直径を求めよ。

外円の半径と中心座標を R, (0, 0)
金円の半径と中心座標を r1, (0, R - r1)
銀円の半径と中心座標を r2, (r2, R - 2r1 -r2), (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r1::positive, r2::positive, 弦::positive, x::positive, x::negative, x2::positive, y2::negative

y = 2R - 2r1
x = sqrt(R^2 - (R - 2r1)^2)
弦 = sqrt(y^2 + x^2)
eq1 = y + sqrt(R^2 - (R - 2r1)^2) - 弦 - 2r2
eq2 = sqrt(R^2 - 弦^2/4) + 2r2 - R |> simplify  # -R + 2*r2 + sqrt(R*r1)
eq3 = y2/x2 * y/x + 1
eq4 = 2sqrt(x2^2 + (y2 + R)^2 - r2^2) - 弦;
res = solve([eq1, eq2, eq3, eq4], (r1, r2, x2, y2))

   2-element Vector{NTuple{4, Sym}}:
    (R*(4 - sqrt(7))/8, R*(4 - sqrt(8 - 2*sqrt(7)))/8, R*(6 - sqrt(-16*sqrt(2)*sqrt(4 - sqrt(7)) - 4*sqrt(14)*sqrt(4 - sqrt(7)) + 8*sqrt(7) + 41))/16, R*(-24 - sqrt(-112*sqrt(2)*sqrt(4 - sqrt(7)) - 28*sqrt(14)*sqrt(4 - sqrt(7)) + 56*sqrt(7) + 287) + 6*sqrt(7) + 4*sqrt(-16*sqrt(2)*sqrt(4 - sqrt(7)) - 4*sqrt(14)*sqrt(4 - sqrt(7)) + 8*sqrt(7) + 41))/48)
    (R*(4 - sqrt(7))/8, R*(4 - sqrt(8 - 2*sqrt(7)))/8, R*(sqrt(-16*sqrt(2)*sqrt(4 - sqrt(7)) - 4*sqrt(14)*sqrt(4 - sqrt(7)) + 8*sqrt(7) + 41) + 6)/16, R*(-24 - 4*sqrt(-16*sqrt(2)*sqrt(4 - sqrt(7)) - 4*sqrt(14)*sqrt(4 - sqrt(7)) + 8*sqrt(7) + 41) + sqrt(-112*sqrt(2)*sqrt(4 - sqrt(7)) - 28*sqrt(14)*sqrt(4 - sqrt(7)) + 56*sqrt(7) + 287) + 6*sqrt(7))/48)

2 組の解が得られるが，2 番目のものが適解である。また，それぞれのパラメータの式は簡約化できる。

res[2][1] |> println
res[2][2] |> sympy.sqrtdenest |> simplify |> println
res[2][3] |> sympy.sqrtdenest |>  simplify |> println
res[2][4] |> sympy.sqrtdenest |>  simplify |> println

   R*(4 - sqrt(7))/8
   R*(5 - sqrt(7))/8
   R*(5 + 2*sqrt(7))/16
   -R*(2 + sqrt(7))/16

金円，銀円の直径は外円の直径の (4 - √7)/8 倍と (5 - √7)/8 倍である。
外円の直径が 10 寸のとき，金円，銀円の直径は 1.6928108611692616寸と 2.942810861169262寸である。

10*(4 - √7)/8, 10*(5 - √7)/8

   (1.6928108611692616, 2.942810861169262)

その他のパラメータは以下の通りである。

   r1 = 0.846405;  r2 = 1.47141;  x2 = 3.21609;  y2 = -1.4518

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 10//2
   (r1, r2, x2, y2) = (R/16) .* (8 - 2√7, 10 - 2√7, 5 + 2√7, -2 - √7)
   y1 = R - 2r1
   x1 = sqrt(R^2 - y1^2)
   弦 = sqrt((2R - 2r1)^2 + (R^2 - y1^2))
   @printf("金円の直径 = %g;  銀円の直径 = %g\n", 2r1, 2r2)
   @printf("r1 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n", r1, r2, x2, y2)
   plot()
   circle(0, 0, R)
   circle(0, R - r1, r1, :blue)
   circle(r2, R - 2r1 - r2, r2, :green)
   circle(-r2, R - 2r1 - r2, r2, :green)
   circle(x2, y2, r2, :green)
   circle(-x2, y2, r2, :green)
   plot!([0, x1, -x1, 0], [-R, y1, y1, -R], color=:black, lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, R, " R", :red, :left, :bottom, delta=delta/2)
       point(0, R - r1, " 金円:r1,(0,R-r1)", :blue, :left, :vcenter)
       point(0, R - 2r1, " R-2r1", :blue, :left, delta=-delta/2)
       point(r2, R - 2r1 - r2, "銀円:r2\n(r2,R-2r1-r2)", :green, :center, delta=-delta/2)
       point(x2, y2, "銀円:r2\n(x2,y2)", :green, :center, delta=-delta/2)
   end
end;

算額（その641）

算額（その641）

長野県飯田市 元善光寺 推定天保15年(1844)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

大小 2 個の正方形が接しており，正方形の頂点を結ぶ線分で分割された領域に，甲円，乙円，丙円を入れる。大小の正方形の面積の我が 113 平方寸，線分の長さが 17 寸のとき，2 個の正方形の一辺の長さ，甲円，乙円，丙円の直径を求めよ。

正方形の一辺の長さを a, b とする。
甲円の半径と中心座標を r1, (r1, r1)
乙円の半径と中心座標を r2, (a - r2, a - r2)
丙円の半径と中心座標を r3, (a + b - r3, b - r3)
とおき，以下の連立方程式を解く。なお，x は頂点を結ぶ線分と小さい方の正方形の上辺の延長線の交わる点の座標 (x, b) である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms A::positive, B::positive, a::positive, b::positive, x::positive, r1::positive, r2::positive, r3::positive

(A, B) = (113, 17)
eq1 = a + (a + b) - sqrt(a^2 + (a + b)^2) - 2r1
eq2 = a + (a - a*b/(a + b)) - sqrt(a^2 + (a - a*b/(a + b))^2) - 2r2
eq3 = (a + b - x) + b - sqrt((a + b - x)^2 + b^2) - 2r3
eq4 = a^2 + b^2 - A
eq5 = a^2 + (a + b)^2 - B^2
eq6 = b/(a + b - x) - (b - a*b/(a + b))/(a - x)
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (a, b, r1, r2, r3, x))

   2-element Vector{NTuple{6, Sym}}:
    (8, 7, 3, 8/5, 21/8, 15/8)
    (22*sqrt(5)/5, 9*sqrt(5)/5, -17/2 + 53*sqrt(5)/10, -187/31 + 583*sqrt(5)/155, -153/44 + 477*sqrt(5)/220, 403*sqrt(5)/110)

算額の問題を解くとき，解が複数個あるのは稀であるが，この問題においては，解は 2 組ある。
正方形の一辺の長さは (8, 7) （上図）

a = 8;  b = 7;  r1 = 3;  r2 = 1.6;  r3 = 2.625;  x = 1.875

と (22/√5, 9/√5) （下図）である。

a = 9.8387;  b = 4.02492;  r1 = 3.35116;  r2 = 2.37824;  r3 = 1.37093;  x = 8.19214

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b, r1, r2, r3, x) = res[n]
   @printf("a = %g;  b = %g;  r1 = %g;  r2 = %g;  r3 = %g;  x = %g\n", a, b, r1, r2, r3, x)
   plot()
   rect(0, 0, a, a, :red)
   rect(a, 0, a + b, b, :blue)
   segment(0, a, a + b , 0, :green)
   circle(r1, r1, r1, :brown)
   circle(a - r2, a - r2, r2, :magenta)
   circle(a + b - r3, b - r3, r3, :black)
   segment(x, b, a, b, :gray70)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(r1, r1, "甲円:r1,(r1,r1)", :brown, :center, delta=-delta/2)
       point(a - r2, a - r2, "乙円:r2\n(a-r2,a-r2)", :magenta, :center, delta=-delta/2)
       point(a + b - r3, b - r3, "丙円:r3\n(a+b-r3,b-r3)", :black, :center, delta=-delta/2)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(a + b, 0, "a+b ", :blue, :right, :bottom, delta=delta/2)
       point(x, b, "(x,b)", :green, :left, :bottom, delta=delta/2)
   end
end;

draw(1, true)
savefig("/Users/aoki/Downloads/fig1.png");

   a = 8;  b = 7;  r1 = 3;  r2 = 1.6;  r3 = 2.625;  x = 1.875


draw(2, true)
savefig("/Users/aoki/Downloads/fig2.png");

   a = 9.8387;  b = 4.02492;  r1 = 3.35116;  r2 = 2.37824;  r3 = 1.37093;  x = 8.19214


 

 

算額（その640）

算額（その640）

長野県伊達市羽広 仲仙寺 文政9年(1826)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

直角三角形内に累円（子円，丑円，寅円,…）が逐次内接し，累円と底辺の隙間に逐円（初円，二円，三円，…，終円）が入っている。初円の直径が 4 寸，終円の直径が 0.5 寸，逐円が 4 個（初円から数えて終円が 4 番目）のときに二円の直径はいかほどか。

子円の半径と中心座標を a0, (a0, a0)
丑円の半径と中心座標を a1, (xa1, a1)
寅円の半径と中心座標を a2, (xa2, a2)...
初円の半径と中心座標を b1, (xb1, b1)
二円の半径と中心座標を b2, (xb2, b2)...
とおき，以下の連立方程式により逐次，各円の半径と中心座標を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms 鈎::positive, 股::positive, 弦::positive,
     a0::positive
@syms xai::positive, ai::positive, xai1::positive, ai1::positive, bi1::positive, xbi1::positive

function func(ai, xai, 股)
   eq1 = (xai1 - xai)^2 + (ai - ai1)^2 - (ai + ai1)^2
   eq2 = (xbi1 - xai)^2 + (ai - bi1)^2 - (ai + bi1)^2
   eq3 = (xai1 - xbi1)^2 + (ai1 - bi1)^2 - (ai1 + bi1)^2
   eq4 = ai/(股 - xai) - ai1/(股 - xai1)
   return solve([eq1, eq2, eq3, eq4], (ai1, xai1, bi1, xbi1))
end

(鈎, 股) = (3, 6)
弦 = sqrt(鈎^2 + 股^2)
a0 = (鈎 + 股 - 弦)/2
println("弦 = $弦;  a0 = $a0")

   弦 = 6.708203932499369;  a0 = 1.1458980337503153

a = Vector{Float64}(undef, 10)
xa = Vector{Float64}(undef, 10)
b = Vector{Float64}(undef, 10)
xb = Vector{Float64}(undef, 10);

(a[1], xa[1], b[1], xb[1]) = func(a0, a0, 股)[1]
for i in 2:10
   (a[i], xa[i], b[i], xb[i]) = func(a[i - 1], xa[i -  1], 股)[1]
end

逐円の半径（直径）は初項 b[1]，公比 b[2]/b[1] の等比数列である（各項の対数を取るとすぐわかる）。
n 番目の逐円の半径は b[1]*(b[2]/b[1])^(n-1) である。

逆に，n 番目の逐円の半径がわかっているが公比がわかっていない場合に，公比 c は以下のようにして求めることができる。
逐円の個数を n，初円径を b1, 終円径を bn とする。

@syms b1, bn, n, c
res = solve(b1*c^(n - 1) - bn, c)[1] |> println

   (bn/b1)^(1/(n - 1))

二円の半径は b1*(bn/b1)^(1/(n - 1)) である。

逐円の個数が n = 4，初円径が b1 = 4, 終円径が bn = 0.5 とすると，公比は 0．5 で，二円の径は 2 である。

n = 4
b1 = 4
bn = 0.5
c = (bn/b1)^(1/(n - 1))
(c, b1*c)

   (0.5, 2.0)

function draw(more=false)
   pyplot(size=(700, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鈎, 股) = (4, 7)
   弦 = sqrt(鈎^2 + 股^2)
   a0 = (鈎 + 股 - 弦)/2
   a = Vector{Float64}(undef, 10)
   xa = Vector{Float64}(undef, 10)
   b = Vector{Float64}(undef, 10)
   xb = Vector{Float64}(undef, 10);
   (a[1], xa[1], b[1], xb[1]) = func(a0, a0, 股)[1]
   for i in 2:10
       (a[i], xa[i], b[i], xb[i]) = func(a[i - 1], xa[i -  1], 股)[1]
   end
   @printf("鈎 = %g;  股 = %g;  弦 = %g;  a0 = %g\n", 鈎, 股, 弦, a0)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:magenta, lw=0.5)
   circle(a0, a0, a0)
   for i in 1:10
       circle(xa[i], a[i], a[i])
       circle(xb[i], b[i], b[i], :blue)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       # vline!([0], color=:black, lw=0.5)
       # hline!([0], color=:black, lw=0.5)
       point(a0, a0, "子", :red, :center, :vcenter, mark=false)
       for (i, char) in enumerate(['丑', '寅', '卯', '辰'])
           point(xa[i], a[i], char, :red, :center, :vcenter, mark=false)
       end
       for (i, char) in enumerate(['初', '二', '三'])
           point(xb[i], b[i], char, :blue, :center, :vcenter, mark=false)
       end
   end
end;

微妙に危うい統計学ページ

この作者のページは，微妙に危ういところが多い。
コメントを付ける手立てがない（ような）ので，ここで指摘する。

【回帰分析】単回帰モデル⑥　Rを利用した分析
https://df-learning.com/regression_model_6

Windows プラットフォームのようで，ファイルを読み込むのに

> #データを読みこむ
> data <- read.csv("D:\\data1.csv")

としているが，"D:/data1.csv" で読み込めるのではないかな?

R スクリプトであるが，注釈行や区切り記号の前後に適切に空白を置くことをおすすめする

> #単回帰モデルの実行
> res=lm(y~x)

以下のように

# 単回帰モデルの実行
res = lm(y ~ x)

> 単回帰直線は𝑦=β1𝑥+β0

β1, β0 は母数で，推定されたのは推定値なので b1, b0 などと書くほうが妥当。

> Prが検定統計量ｔより大きくなる確率を表している。
> 𝐻0:β0=0と仮定したとき
> 𝐵̂ 0=−8.23以下になる確率は0.082
> 𝐻1:β1=0と仮定したとき
> 𝐵̂ 0=0.01以上になる確率は0.00253

これらはすべて誤り。特に H0, H1 の使い方は常軌を逸している。
H0 は帰無仮説，H1 は対立仮説を表す。添字は帰無仮説の順番を表すのではない。

> 𝐻0:β0=0と仮定したとき
> b0=−8.23「よりも極端な値を取る」確率は0.082

> 𝐻0:β1=0と仮定したとき
> b0=0.01「よりも極端な値を取る」確率は0.00253

> β0は　.　なので有意水準0.1つまり10%で有意である

「10％有意」などというのは使わないほうがよい。

> 特性値yと焼成温度xの関係性はないとは否定できない

二重否定をするのは，「帰無仮説を棄却できるとは言えない」というとき。

特性値yと焼成温度xの関係性はない（帰無仮説が棄却される場合）

特性値yと焼成温度xの関係性はないとはいえない（二重否定。帰無仮説を棄却できない場合）

どなたか，件のページ（作者）に直接コメントする手立てをご存じの方は教えてください。

 

算額（その639）

算額（その639）

長野県伊那市羽広 仲仙寺 文政9年(1826)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

長方形内に長さ 45 寸の甲弦（赤），長さ 36 寸の乙弦（青）がある。これらが交差してできる三角形の辺（大斜，中斜，小斜）の長さを求めよ。

長方形の長辺と短辺を a, b とする。
小斜の両端の座標を (x1, y1), (x2, y2) として，以下の連立方程式を解く。

本質的には eq1, eq2 で a, b を求めれば，eq3 〜 eq6 は使わなくても大斜，中斜，小斜を求める事ができるし，eq7 〜 eq8 は不要である。
条件として与えられる 2 つの数値を A，B として一般解を求めてみる。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms x1::positive, y1::positive, x2::positive, y2::positive, a::positive, b::positive,
     大斜, 中斜, 小斜, A, B

eq1 = a^2 + b^2 - A^2
eq2 = a^2 + (b/2)^2 - B^2
eq3 = (b - y1)/x1 - b/a
eq4 = (y1 - b/2)/x1 - (b - y1)/(a - x1)
eq5 = (b - y2)/x2 - (b/2)/a
eq6 = (b - y1)/(a - x1) - (b - y2)/(a - x2)
eq7 = 大斜 - sqrt(x2^2 + (b - y2)^2)
eq8 = 中斜 - sqrt(x1^2 + (b - y1)^2)
eq9 = 小斜 - sqrt((x2 - x1)^2 + (y2 - y1)^2)

res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (大斜, 中斜, 小斜, a, b, x1, y1, x2, y2))

   4-element Vector{NTuple{9, Sym}}:
    (sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, -sqrt(-3*A^2 + 12*B^2)/3, -2*sqrt(3*A^2 - 3*B^2)/3, -sqrt(-3*A^2 + 12*B^2)/9, -4*sqrt(3*A^2 - 3*B^2)/9, -sqrt(-3*A^2 + 12*B^2)/6, -sqrt(3*A^2 - 3*B^2)/2)
    (sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, -sqrt(-3*A^2 + 12*B^2)/3, 2*sqrt(3*A^2 - 3*B^2)/3, -sqrt(-3*A^2 + 12*B^2)/9, 4*sqrt(3*A^2 - 3*B^2)/9, -sqrt(-3*A^2 + 12*B^2)/6, sqrt(3*A^2 - 3*B^2)/2)
    (sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, sqrt(-3*A^2 + 12*B^2)/3, -2*sqrt(3*A^2 - 3*B^2)/3, sqrt(-3*A^2 + 12*B^2)/9, -4*sqrt(3*A^2 - 3*B^2)/9, sqrt(-3*A^2 + 12*B^2)/6, -sqrt(3*A^2 - 3*B^2)/2)
    (sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, sqrt(-3*A^2 + 12*B^2)/3, 2*sqrt(3*A^2 - 3*B^2)/3, sqrt(-3*A^2 + 12*B^2)/9, 4*sqrt(3*A^2 - 3*B^2)/9, sqrt(-3*A^2 + 12*B^2)/6, sqrt(3*A^2 - 3*B^2)/2)

4 番目のものが適解である。

大斜，中斜，小斜は B/2 = 18, A/3 = 15, B/6 = 6 である。

他のパラメータは以下の通り。

(A, B) = (45, 36)
(sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, sqrt(-3*A^2 + 12*B^2)/3, 2*sqrt(3*A^2 - 3*B^2)/3, sqrt(-3*A^2 + 12*B^2)/9, 4*sqrt(3*A^2 - 3*B^2)/9, sqrt(-3*A^2 + 12*B^2)/6, sqrt(3*A^2 - 3*B^2)/2)

   (18.0, 15.0, 6.0, 32.449961479175904, 31.176914536239792, 10.816653826391967, 20.784609690826528, 16.224980739587952, 23.382685902179844)

大斜 = 18;  中斜 = 15;  小斜 = 6
a = 32.45;  b = 31.1769;  x1 = 10.8167;  y1 = 20.7846;  x2 = 16.225;  y2 = 23.3827

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (A, B) = (45, 36)
   (大斜, 中斜, 小斜, a, b, x1, y1, x2, y2) = (sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, sqrt(-3*A^2 + 12*B^2)/3, 2*sqrt(3*A^2 - 3*B^2)/3, sqrt(-3*A^2 + 12*B^2)/9, 4*sqrt(3*A^2 - 3*B^2)/9, sqrt(-3*A^2 + 12*B^2)/6, sqrt(3*A^2 - 3*B^2)/2)
   plot([0, a, a, 0, 0], [0, 0, b, b, 0], color=:green, lw=0.5)
   segment(0, b, a, 0, :red)
   segment(0, b/2, a, b, :blue)
   segment(0, b, a, b/2, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x1, y1, "  (x1,y1)", :black, :left, :vcenter)
       point(x2, y2, "  (x2,y2)", :black, :left, :vcenter)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, b/2, " b/2", :blue, :left, :top, delta=-delta/2)
       point(a, b/2, "", :blue, :left, :top, delta=-delta/2)
       point(0, b, " b", :blue, :left, :bottom, delta=delta/2)
   end
end;