算額(その639)
長野県伊那市羽広 仲仙寺 文政9年(1826)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
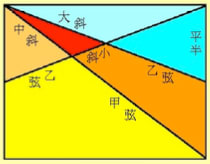
長方形内に長さ 45 寸の甲弦(赤),長さ 36 寸の乙弦(青)がある。これらが交差してできる三角形の辺(大斜,中斜,小斜)の長さを求めよ。
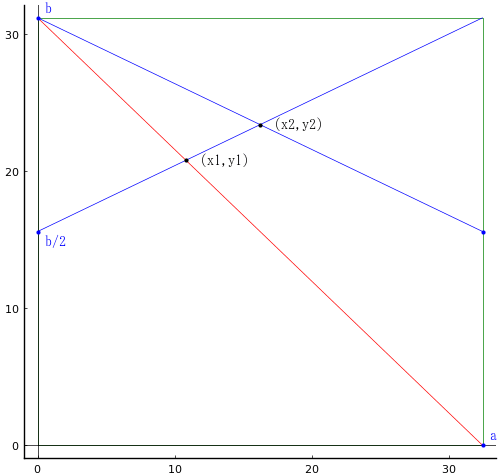
長方形の長辺と短辺を a, b とする。
小斜の両端の座標を (x1, y1), (x2, y2) として,以下の連立方程式を解く。
本質的には eq1, eq2 で a, b を求めれば,eq3 〜 eq6 は使わなくても大斜,中斜,小斜を求める事ができるし,eq7 〜 eq8 は不要である。
条件として与えられる 2 つの数値を A,B として一般解を求めてみる。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms x1::positive, y1::positive, x2::positive, y2::positive, a::positive, b::positive,
大斜, 中斜, 小斜, A, B
eq1 = a^2 + b^2 - A^2
eq2 = a^2 + (b/2)^2 - B^2
eq3 = (b - y1)/x1 - b/a
eq4 = (y1 - b/2)/x1 - (b - y1)/(a - x1)
eq5 = (b - y2)/x2 - (b/2)/a
eq6 = (b - y1)/(a - x1) - (b - y2)/(a - x2)
eq7 = 大斜 - sqrt(x2^2 + (b - y2)^2)
eq8 = 中斜 - sqrt(x1^2 + (b - y1)^2)
eq9 = 小斜 - sqrt((x2 - x1)^2 + (y2 - y1)^2)
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (大斜, 中斜, 小斜, a, b, x1, y1, x2, y2))
4-element Vector{NTuple{9, Sym}}:
(sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, -sqrt(-3*A^2 + 12*B^2)/3, -2*sqrt(3*A^2 - 3*B^2)/3, -sqrt(-3*A^2 + 12*B^2)/9, -4*sqrt(3*A^2 - 3*B^2)/9, -sqrt(-3*A^2 + 12*B^2)/6, -sqrt(3*A^2 - 3*B^2)/2)
(sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, -sqrt(-3*A^2 + 12*B^2)/3, 2*sqrt(3*A^2 - 3*B^2)/3, -sqrt(-3*A^2 + 12*B^2)/9, 4*sqrt(3*A^2 - 3*B^2)/9, -sqrt(-3*A^2 + 12*B^2)/6, sqrt(3*A^2 - 3*B^2)/2)
(sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, sqrt(-3*A^2 + 12*B^2)/3, -2*sqrt(3*A^2 - 3*B^2)/3, sqrt(-3*A^2 + 12*B^2)/9, -4*sqrt(3*A^2 - 3*B^2)/9, sqrt(-3*A^2 + 12*B^2)/6, -sqrt(3*A^2 - 3*B^2)/2)
(sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, sqrt(-3*A^2 + 12*B^2)/3, 2*sqrt(3*A^2 - 3*B^2)/3, sqrt(-3*A^2 + 12*B^2)/9, 4*sqrt(3*A^2 - 3*B^2)/9, sqrt(-3*A^2 + 12*B^2)/6, sqrt(3*A^2 - 3*B^2)/2)
4 番目のものが適解である。
大斜,中斜,小斜は B/2 = 18, A/3 = 15, B/6 = 6 である。
他のパラメータは以下の通り。
(A, B) = (45, 36)
(sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, sqrt(-3*A^2 + 12*B^2)/3, 2*sqrt(3*A^2 - 3*B^2)/3, sqrt(-3*A^2 + 12*B^2)/9, 4*sqrt(3*A^2 - 3*B^2)/9, sqrt(-3*A^2 + 12*B^2)/6, sqrt(3*A^2 - 3*B^2)/2)
(18.0, 15.0, 6.0, 32.449961479175904, 31.176914536239792, 10.816653826391967, 20.784609690826528, 16.224980739587952, 23.382685902179844)
大斜 = 18; 中斜 = 15; 小斜 = 6
a = 32.45; b = 31.1769; x1 = 10.8167; y1 = 20.7846; x2 = 16.225; y2 = 23.3827
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(A, B) = (45, 36)
(大斜, 中斜, 小斜, a, b, x1, y1, x2, y2) = (sqrt(B^2)/2, sqrt(A^2)/3, sqrt(B^2)/6, sqrt(-3*A^2 + 12*B^2)/3, 2*sqrt(3*A^2 - 3*B^2)/3, sqrt(-3*A^2 + 12*B^2)/9, 4*sqrt(3*A^2 - 3*B^2)/9, sqrt(-3*A^2 + 12*B^2)/6, sqrt(3*A^2 - 3*B^2)/2)
plot([0, a, a, 0, 0], [0, 0, b, b, 0], color=:green, lw=0.5)
segment(0, b, a, 0, :red)
segment(0, b/2, a, b, :blue)
segment(0, b, a, b/2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(x1, y1, " (x1,y1)", :black, :left, :vcenter)
point(x2, y2, " (x2,y2)", :black, :left, :vcenter)
point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
point(0, b/2, " b/2", :blue, :left, :top, delta=-delta/2)
point(a, b/2, "", :blue, :left, :top, delta=-delta/2)
point(0, b, " b", :blue, :left, :bottom, delta=delta/2)
end
end;




















