算額（その658）

算額（その658）

埼玉県東松山市岩殿 正法寺（岩殿観音） 明治11年(1878)
山口正義：毛呂周辺の算額
https://yamabukiwasan.sakura.ne.jp/22moroshuuhen.pdf
山口正義：やまぶき，和算と歴史随想 からリンク
https://yamabukiwasan.sakura.ne.jp/page3.html

大円の中に 4 本の斜線を引き，分割された領域に甲円 2 個，乙円 2 個，丙円 4 個を入れる。乙円の直径がわかっているときに丙円の直径を求めよ。

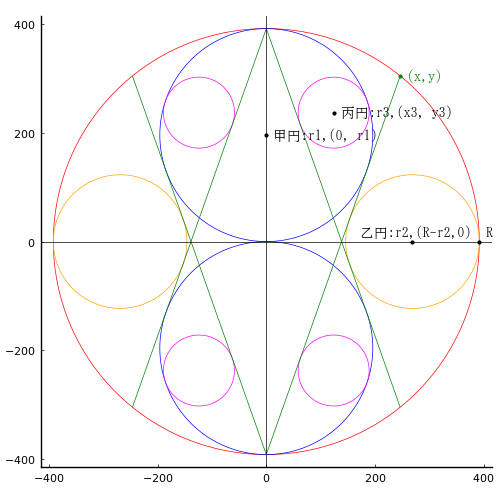
大円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - r1), (0, r1 - R)
乙円の半径と中心座標を r2, (R - r2, 0)
丙円の半径と中心座標を r3, (x3, y3)
とおき以下の連立方程式を解く。

未知数は R, r3, x3, y3, x で，以下の 5 個の方程式を立てる。連立方程式を解いた式には r2 が含まれる（任意の r2 でそれぞれのパラメータが計算できる）。

SymPy の性能上，連立方程式を一度に解くことができないが，個々の方程式の独立性を考えて以下のように順次といてゆく。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, y3::positive,
     x, y
# r2 = 1　最終的な未知数として，解に含まれる
r1 = R/2
y = sqrt(R^2 - x^2)

eq1 = x3^2 + (y3 - r1)^2 - (r1 - r3)^2
eq2 = dist(0, -R, x, y, 0, R - r1) - r1^2
eq3 = dist(0, -R, x, y, R - r2, 0) - r2^2
eq4 = 2*sqrt(r1^2 - (r1 - 2r3)^2) - sqrt((2r1)^2 - (2r1/3)^2)
eq5 = (y3 - r1)/x3 - 1//3;

まず最初に R と x を求めるために eq2, eq3 の連立方程式を解くが，これも SymPy の性能上解けないので，まず eq2 を x について解く。

res1 = solve(eq2, x) |>  println  # x

   Sym[-4*sqrt(2)*R/9, 4*sqrt(2)*R/9]

2 番目のものが適解である。x, およびそれにより計算される y を用いて eq3 を書き直す。

x = 4*sqrt(Sym(2))*R/9
y = sqrt(R^2 - x^2)
eq3 = dist(0, -R, x, y, R - r2, 0) - r2^2;

R について解く。2 番目の解が適解である。

res2 = solve(eq3, R)
res2 |> println

   Sym[-3*r2/sqrt(9 - 4*sqrt(2)) + 2*r2*(-4 + sqrt(2))/(-9 + 4*sqrt(2)), 2*r2*(-4 + sqrt(2))/(-9 + 4*sqrt(2)) + 3*r2/sqrt(9 - 4*sqrt(2))]

res2[1](r2 => 1).evalf(), res2[2](r2 => 1).evalf()  # 2 番目が適解

   (-0.0938363213560543, 3.18767264271211)

2 番目の解を簡約化する。

res2[2] |> sympy.sqrtdenest |> simplify |> println  # R

   11*r2/7 + 8*sqrt(2)*r2/7

R, x, y を書き直す。なお，r1 は R の 1/2 である。

R = 11*r2/7 + 8*sqrt(Sym(2))*r2/7
x = 4*sqrt(Sym(2))*R/9
y = 7*R/9
r1 = R/2;

ここまでで，r3 は以下のように単純に求めることができるようになる。最初の解が適解である。r3 は 大円の半径の 1/ 6 である

res3 = solve(eq4, r3)[1]  # r3
res3 |> println

   R/6

eq1, eq5 の連立方程式を解けば乙円の中心座標 (x3, y3) が求まる。
2 組の解が求まるが，2 番目のものが適解である。

eq1 = x3^2 + (y3 - r1)^2 - (r1 - r3)^2
eq5 = (y3 - r1)/x3 - 1//3;
res4 = solve([eq1, eq5], (x3, y3))

   1-element Vector{Tuple{Sym, Sym}}:
    (3*sqrt(1760*sqrt(2)*r2^2 + 2490*r2^2 - 2240*sqrt(2)*r2*r3 - 3080*r2*r3 + 1960*r3^2)/140, r2*(11 + 8*sqrt(2))/14 + sqrt(1760*sqrt(2)*r2^2 + 2490*r2^2 - 2240*sqrt(2)*r2*r3 - 3080*r2*r3 + 1960*r3^2)/140)

以上をまとめると，
乙円の半径を r2 とする。
大円の半径 R が決まる。R = 11*r2/7 + 8*sqrt(2)*r2/7
(x, y) が決まる。x = 4*sqrt(2)*R/9，y = 7*R/9
丙円の半径が決まる。r3 = R/6
丙円の中心座標が決まる。(x3, y3) = (3*sqrt(10)*(R - 2*r3)/20, R/2 + sqrt(10)*(R - 2*r3)/20)

r2 = 1
R = 11*r2/7 + 8*sqrt(2)*r2/7
r1 = R/2
(x, y) = (4*sqrt(2)*R/9, 7*R/9)
r3 = R/6
(x3, y3) = (3*sqrt(10)*(R - 2*r3)/20, R/2 + sqrt(10)*(R - 2*r3)/20)
@printf("r2 = %g;  R = %g;  r3 = %g;  x3 = %g;  y3 = %g;  x = %g;  y = %g\n", r2, R, r3, x3, y3, x, y)

   r2 = 1;  R = 3.18767;  r3 = 0.531279;  x3 = 1.00803;  y3 = 1.92985;  x = 2.00358;  y = 2.4793

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 123
   R = 11*r2/7 + 8*sqrt(2)*r2/7
   r1 = R/2
   (x, y) = (4*sqrt(2)*R/9, 7*R/9)
   r3 = R/6
   (x3, y3) = (3*sqrt(10)*(R - 2*r3)/20, R/2 + sqrt(10)*(R - 2*r3)/20)
   @printf("r2 = %g;  R = %g;  r3 = %g;  x3 = %g;  y3 = %g;  x = %g;  y = %g\n", r2, R, r3, x3, y3, x, y)
   plot()
   circle(0, 0, R)
   circle(0, r1, r1, :blue)
   circle(0, -r1, r1, :blue)
   circle(R - r2, 0, r2, :orange)
   circle(r2 - R, 0, r2, :orange)
   circle4(x3, y3, r3, :magenta)
   plot!([-x, 0, x], [-y, R, -y], color=:green, lw=0.5)
   plot!([-x, 0, x], [y, -R, y], color=:green, lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x, y, " (x,y)", :green, :left, :vcenter)
       point(0, r1, " 甲円:r1,(0, r1)", :black, :left, :vcenter)
       point(R - r2, 0, " 乙円:r2,(R-r2,0)", :black, :center, :bottom, delta=delta/2)
       point(x3, y3, " 丙円:r3,(x3, y3)", :black, :left, :vcenter)
       point(R, 0, " R", :black, :left, :bottom, delta=delta/2)
   end
end;