算額（その868）

算額（その868）

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究-算額を―算額を用いた課題学習とそのフィールドワークの実践から―，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

"たばや"の算額
https://www.libe.nara-k.ac.jp/~yano/ketcindy/sangaku_tabaya.html

大円の中に，甲円と乙円を入れる。大円に接し，甲円と乙円に外接する丙円を描く。次に，大円に接し，甲円と丙円に外接する丁円を描く。同じ手順で，戊円，己円...を描くことができる。大円，甲円の直径がそれぞれ 16 寸，9.6 寸のとき，乙円，丙円，丁円の直径を求めよ。

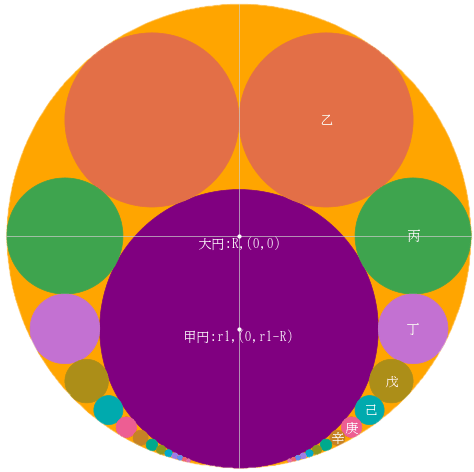
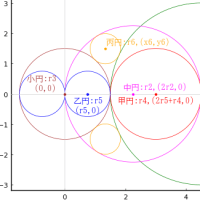
大円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, r1 - R)
乙円の半径と中心座標を r2, (x2, y2); x2 = r2
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (x4, x5)
とおき，以下のように方程式を解いてゆく。

1.　乙円の半径と中心座標を求める

大円と甲円の半径が既知なので，乙円の半径と中心座標は次の二元連立方程式を解けばよい。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive,
     r2::positive, x2::positive, y2::positive

x2 = r2
eq1 = r2^2 + y2^2 - (R - r2)^2
eq2 = r2^2 + (y2 - r1 + R)^2 - (r1 + r2)^2
res1 = solve([eq1, eq2], (r2, y2))[1]

   (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))

2.　丙円の半径と中心座標を求める

乙円までは半径と中心座標が決まったので，次の累円（丙円）の半径と中心座標は次の三元連立方程式を解けばよい。

@syms r3::positive, x3::positive, y3::real

eq3 = x3^2 + y3^2 - (R - r3)^2
eq4 = x3^2 + (y3 - r1 + R)^2 - (r1 +r3)^2
eq5 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2;
res2 = solve([eq3, eq4, eq5], (r3, x3, y3));
# res2[1]

2 組の解が得られるが，2 番目のものが適解である。
求める累円の前にある累円（甲円）の半径と中心座標から，求めるべき累円（乙円）の半径と中心座標が得られる。
この関係式は前の累円と次の累円の関係式なので，次々に適用することで，累円の半径と中心座標を決定していくことができる。

3.　丙円以降の半径と中心座標を求める

これを関数にすると以下のようなものになる。

nextcircle(R, r1, r2, x2, y2) = ((R^6 - R^5*r1 + R^5*r2 + 3*R^5*y2 - R^4*r1^2 - R^4*r1*r2 - R^4*r1*y2 - R^4*r2^2 + 2*R^4*r2*y2 + R^4*x2^2 + 3*R^4*y2^2 + R^3*r1^3 - R^3*r1^2*r2 - 3*R^3*r1^2*y2 + R^3*r1*r2^2 - 2*R^3*r1*r2*y2 + 3*R^3*r1*x2^2 + R^3*r1*y2^2 - R^3*r2^3 - R^3*r2^2*y2 + R^3*r2*x2^2 + R^3*r2*y2^2 + R^3*x2^2*y2 + R^3*y2^3 - 2*R^2*sqrt(r1)*x2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + R^2*r1^3*r2 + R^2*r1^3*y2 + R^2*r1^2*r2^2 - 2*R^2*r1^2*r2*y2 - R^2*r1^2*x2^2 - 3*R^2*r1^2*y2^2 + R^2*r1*r2^3 - R^2*r1*r2^2*y2 - R^2*r1*r2*x2^2 - R^2*r1*r2*y2^2 + R^2*r1*x2^2*y2 + R^2*r1*y2^3 - R*r1^3*r2^2 + 2*R*r1^3*r2*y2 - 3*R*r1^3*x2^2 - R*r1^3*y2^2 + R*r1^2*r2^3 + R*r1^2*r2^2*y2 - R*r1^2*r2*x2^2 - R*r1^2*r2*y2^2 - R*r1^2*x2^2*y2 - R*r1^2*y2^3 + 2*r1^(5/2)*x2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) - r1^3*r2^3 + r1^3*r2^2*y2 + r1^3*r2*x2^2 + r1^3*r2*y2^2 - r1^3*x2^2*y2 - r1^3*y2^3)/(2*(R^5 - R^4*r1 + 2*R^4*r2 + 2*R^4*y2 - R^3*r1^2 - 2*R^3*r1*r2 + 2*R^3*r1*y2 + R^3*r2^2 + 2*R^3*r2*y2 + R^3*y2^2 + R^2*r1^3 - 2*R^2*r1^2*r2 - 2*R^2*r1^2*y2 - R^2*r1*r2^2 + 2*R^2*r1*r2*y2 + 4*R^2*r1*x2^2 + 3*R^2*r1*y2^2 + 2*R*r1^3*r2 - 2*R*r1^3*y2 - R*r1^2*r2^2 - 2*R*r1^2*r2*y2 + 4*R*r1^2*x2^2 + 3*R*r1^2*y2^2 + r1^3*r2^2 - 2*r1^3*r2*y2 + r1^3*y2^2)), (R^3*sqrt(r1)*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R^3*r1^2*x2 - 2*R^3*r1*r2*x2 + 2*R^3*r1*x2*y2 + R^2*sqrt(r1)*r2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + R^2*sqrt(r1)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R^2*r1^3*x2 - 2*R^2*r1*r2^2*x2 + 2*R^2*r1*x2^3 + 2*R^2*r1*x2*y2^2 - R*r1^(5/2)*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R*r1^(3/2)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R*r1^3*r2*x2 - 2*R*r1^3*x2*y2 - 2*R*r1^2*r2^2*x2 + 2*R*r1^2*x2^3 + 2*R*r1^2*x2*y2^2 - r1^(5/2)*r2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + r1^(5/2)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)))/(R^5 - R^4*r1 + 2*R^4*r2 + 2*R^4*y2 - R^3*r1^2 - 2*R^3*r1*r2 + 2*R^3*r1*y2 + R^3*r2^2 + 2*R^3*r2*y2 + R^3*y2^2 + R^2*r1^3 - 2*R^2*r1^2*r2 - 2*R^2*r1^2*y2 - R^2*r1*r2^2 + 2*R^2*r1*r2*y2 + 4*R^2*r1*x2^2 + 3*R^2*r1*y2^2 + 2*R*r1^3*r2 - 2*R*r1^3*y2 - R*r1^2*r2^2 - 2*R*r1^2*r2*y2 + 4*R*r1^2*x2^2 + 3*R*r1^2*y2^2 + r1^3*r2^2 - 2*r1^3*r2*y2 + r1^3*y2^2), -sqrt(r1)*x2*sqrt(-R*(-R^2 - 2*R*r2 - r2^2 + x2^2 + y2^2)*(R^2 - 2*R*r1 + 2*R*y2 + 2*r1*r2 - 2*r1*y2 - r2^2 + x2^2 + y2^2))*(R + r1)/(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 + R^2*r1^2 - 4*R^2*r1*r2 + R^2*r2^2 + 2*R^2*r2*y2 + R^2*y2^2 + 2*R*r1^2*r2 - 2*R*r1^2*y2 - 2*R*r1*r2^2 + 4*R*r1*x2^2 + 2*R*r1*y2^2 + r1^2*r2^2 - 2*r1^2*r2*y2 + r1^2*y2^2) + (-R^5 + 4*R^4*r1 - 3*R^4*r2 - R^4*y2 - 3*R^3*r1^2 + 8*R^3*r1*r2 + 2*R^3*r1*y2 - 3*R^3*r2^2 - 2*R^3*r2*y2 + R^3*x2^2 + R^3*y2^2 - 5*R^2*r1^2*r2 + 3*R^2*r1^2*y2 + 4*R^2*r1*r2^2 - 4*R^2*r1*x2^2 - R^2*r2^3 - R^2*r2^2*y2 + R^2*r2*x2^2 + R^2*r2*y2^2 + R^2*x2^2*y2 + R^2*y2^3 - R*r1^2*r2^2 + 2*R*r1^2*r2*y2 + 3*R*r1^2*x2^2 - R*r1^2*y2^2 - 2*R*r1*r2^2*y2 + 2*R*r1*x2^2*y2 + 2*R*r1*y2^3 + r1^2*r2^3 - r1^2*r2^2*y2 - r1^2*r2*x2^2 - r1^2*r2*y2^2 + r1^2*x2^2*y2 + r1^2*y2^3)/(2*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 + R^2*r1^2 - 4*R^2*r1*r2 + R^2*r2^2 + 2*R^2*r2*y2 + R^2*y2^2 + 2*R*r1^2*r2 - 2*R*r1^2*y2 - 2*R*r1*r2^2 + 4*R*r1*x2^2 + 2*R*r1*y2^2 + r1^2*r2^2 - 2*r1^2*r2*y2 + r1^2*y2^2)));

順次適用した結果を表示すると以下のようになる。
大円，甲円の直径がそれぞれ 16 寸，9.6 寸 なので，乙円の，半径と中心座標は以下のようになる。

res1

   (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))

res1[1](R => 16/2, r1 => 9.6/2) |> N  # r2 = x2

   3.0

res1[2](R => 16/2, r1 => 9.6/2) |> N  # y2

   3.999999999999999

nextcircle(16/2, 9.6/2, 3, 3, 4)  # r3, x3, y3

   (2.0000000000000004, 5.999999999999999, 0.0)

nextcircle(16/2, 9.6/2, 2, 6, 0)  # r4, x4, y4

   (1.2000000000000002, 6.000000000000001, -3.2000000000000006)

nextcircle(16/2, 9.6/2, 1.2, 6, -3.2) # r5, x5, y5

   (0.7499999999999988, 5.250000000000001, -4.999999999999999)

nextcircle(16/2, 9.6/2, 0.75, 5.25, -5)  # r6, x6, y6

   (0.5000000000000001, 4.499999999999999, -6.000000000000001)

乙円，丙円，丁円の直径は 2r2 = 6 寸, 2r3 = 4　寸, 2r4 = 2.4 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r1) = (160, 96) .// 20
   (r2, y2) = (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))
   x2 = r2
   plot(showaxis=false)
   delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
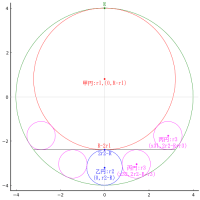
   circlef(0, 0, R, :orange)
   circlef(0, r1 - R, r1, :purple)
   names = Char["甲乙丙丁戊己庚辛壬癸"...]
   @printf("%g %g %g %g\n", 1, r1, 0, r1 - R)
   for i = 2:15
       @printf("%g %g %g %g\n", i, r2, x2, y2)
       if i <= 8
           notation = @sprintf("%s円:r%g,(x%g,y%g)", names[i], i, i, i)
           point(x2, y2, names[i], :white, :center, :vcenter)
       end
       circlef(x2, y2, r2, i)
       circlef(-x2, y2, r2, i)
       r2, x2, y2 = nextcircle(R, r1, r2, x2, y2)
   end

   if more        
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 0, "大円:R,(0,0)", :white, :center, delta=-2delta)
       point(0, r1 - R, "甲円:r1,(0,r1-R)", :white, :center, delta=-2delta)
   end
end;

   1 4.8 0 -3.2
   2 3 3 4
   3 2 6 0
   4 1.2 6 -3.2
   5 0.75 5.25 -5
   6 0.5 4.5 -6
   7 0.352941 3.88235 -6.58824
   8 0.26087 3.3913 -6.95652
   9 0.2 3 -7.2
   10 0.157895 2.68421 -7.36842
   11 0.12766 2.42553 -7.48936
   12 0.105263 2.21053 -7.57895
   13 0.0882353 2.02941 -7.64706
   14 0.075 1.875 -7.7
   15 0.0645161 1.74194 -7.74194

4.　直径だけを求める場合

累円の直径（半径）だけを逐次求めるには，算法助術の公式55 を使えばよい。

using SymPy
@syms d1, d2, d3, d4, R, r1, r2, r3, r4
(d1, d2, d3) = (R, r1, r2)
eq55 = d1^2*d2^2*d3^2 + d1^2*d4^2*(d2 - d3)^2 + 2*d1*d2^2*d3^2*d4 - 2*d1*d2*d3*d4*(d1 - d4)*(d2 + d3) + d2^2*d3^2*d4^2;

外円 R に内接し，甲円 r1 と i 番目の累円 r(i)に接する r(i+1) 番目の累円の半径 d4 は，eq55 を 解けば求めることができる。

res = solve(eq55, d4)[1]
res |> println

   (R*r1*r2*(R*r1 + R*r2 - r1*r2) - 2*sqrt(-R^3*r1^3*r2^3*(-R + r1 + r2)))/(R^2*r1^2 - 2*R^2*r1*r2 + R^2*r2^2 + 2*R*r1^2*r2 + 2*R*r1*r2^2 + r1^2*r2^2)

これを関数にすれば，（外円，甲円と）乙円を初期値として，次の円の半径を求めることができる。

nxt(R, r1, r2) = (R*r1*r2*(R*r1 + R*r2 - r1*r2) - 2*sqrt(-R^3*r1^3*r2^3*(-R + r1 + r2)))/(R^2*r1^2 - 2*R^2*r1*r2 + R^2*r2^2 + 2*R*r1^2*r2 + 2*R*r1*r2^2 + r1^2*r2^2);

(R, r1) = (160, 96) .// 20
r = 3  # r2 から始める
for i = 2:15
   @printf("%g %g\n", i, r)
   r = nxt(R, r1, r)  # i = 2 のとき r3 が求まる
end

   2 3
   3 2
   4 1.2
   5 0.75
   6 0.5
   7 0.352941
   8 0.26087
   9 0.2
   10 0.157895
   11 0.12766
   12 0.105263
   13 0.0882353
   14 0.075
   15 0.0645161