2月23日 白夜と極夜(太陽が空に出ない日)について
2006年9月21日に発表致しました記事(機械工学関連>第3角法による作図の効用>例2)は、少し判然としないところが有りましたので、以下に補記します。
これは、緯度80°の地帯一帯- -即ち曲線の円(Aとする)- -を1つの物体と認めたもので、円周上を運行する、地球の中心と、太陽との中心角(春分点を基準とした中心角)をαとして
、プラスの方向は反時計方向とする。
次に、地球については、1ページの様に座標を採用している。地球のZ軸周りの回転方向φは、プラスの方向は、上から見て、反時計方向とする。(上から見た地球の自転方向と同じ)
キーポイントは以下
7/10ページの直線(OA’)は、3ページのy1に相当する。 (白夜に対応-4月23日に相当)
―> α=25.816°の線はx1軸に相当する
7/10ページの直線(OA’')は、同様に
―> α=-25.816°の線はx1軸に相当する。(極夜に対応-2月25日に相当)
以下の説明で、明確になります。

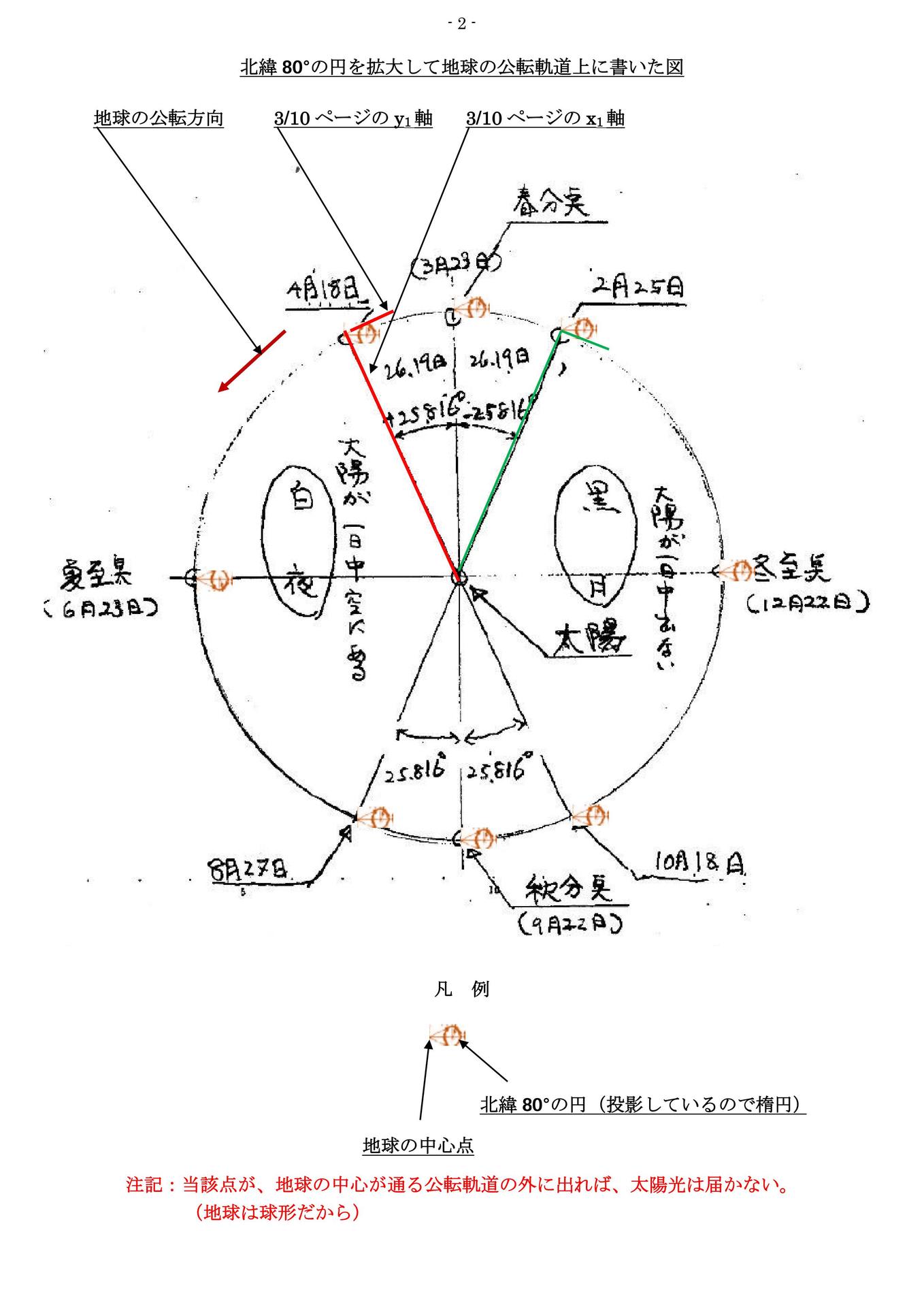

上図の4月18日の時点で、緯度80°の点は全て、白夜になっています。また地球の公転周期は365.25日ですから、1年に1/4日分ほどずれますから、閏年の前などは3/4日違っています。それは、基準となる春分の日の差になってきます。地球は約26,000年周期で歳差運動をしていますが、これは、春分点がごく僅かづつ、公転軌道上で移動していくことなので、白夜や極夜の日付けへの影響は無いのです。実際にはwikipediaによれば、北緯78°のsvalbard諸島では白夜は、4月20日に始まり、8月22日に終わるとなっています。これは私が春分点を3月23日(実際は3月21日とすべき)と設定している(これを考慮すると、私の計算では、白夜は4月16日に始まり、8月25日に終わることになります)のと緯度を78°として、この方法で計算すると、4月22日に始まり、8月20日に終わることになります。この計算と実際の2日の差の中の0.5日は、光の屈折によるものです。角度でも0.5°です。また0.25日は太陽の大きさの影響で、角度で約0.25°です。日に直すと同じく0.25日となります。(地球の公転軌道の半径は約1億5千万km、太陽の直径は約140万km、地球の直径は、約12,750 kmです)他には、地球はほぼ回転楕円体であること、当該地の地形や、測定地点(svalbard諸島のどの地点か)が丁度緯度78°であったのか、等にもよります。緯度が2°低くなったために、白夜の期間は6日遅く始まり、5日早く終わりことになります。
合掌
南無阿弥陀仏 南無阿弥陀仏
追記
1.厳密に、数学的に解くのであれば、下図に示す、POWER(X,2)+POWER(Y,2)=POWER((2.3*POWER(10,4)),2)- - -の地球の公転軌道円)と
POWER((X+a*cosθ),2)/POWER(0.17365,2)+POWER((Y+a:sinθ-0.39269),2)/POWER(0.15925,2)=1の楕円とが接するときの θ の値を求めることですが、この解は非常に計算が面倒である。それよりも、このようにしても十分な精度の計算が出来る。何故かというと、地球の半径を1とすると、地球が太陽の周りを回る公転軌道の半径は2.3*POWER(10,4)となり、上の様に円周を直線と考えても良いからです。これらの円と楕円が接する厳密解は θ=25.817°であり0.001°だけ増加しているだけなのです。
また、ここでのφは、地球の自転角度ではなく、緯度80°の各点の位相角だと考えて下さい。地球の自転の位相角度と公転の位相角度とは、関数関係にあるから、θ=一定ならば、φも一定であるからです。φを各点の位相角と考えれば、θとφは関数関係にはなく、任意の角度を取り得るからです。

2. 以上は地球は等速で公転軌道を動くとして計算しましたが、実際は、下図の様に公転軌道は楕円ですから、また公転速度はケプラーの面積法則によって、等しい時間で、動径が描く面積は等しくなるように公転しますので、春分点は以下の様な点にあると考えられます。これ以上、現実に近い計算をするには、実際の楕円の公転軌道を使い、今年は、春分点が公転軌道のどこにあるかを決定し、公転速度もケプラーの面積法則を使う、厳密解をしなければならないかも知れません。

2006年9月21日に発表致しました記事(機械工学関連>第3角法による作図の効用>例2)は、少し判然としないところが有りましたので、以下に補記します。
これは、緯度80°の地帯一帯- -即ち曲線の円(Aとする)- -を1つの物体と認めたもので、円周上を運行する、地球の中心と、太陽との中心角(春分点を基準とした中心角)をαとして
、プラスの方向は反時計方向とする。
次に、地球については、1ページの様に座標を採用している。地球のZ軸周りの回転方向φは、プラスの方向は、上から見て、反時計方向とする。(上から見た地球の自転方向と同じ)
キーポイントは以下
7/10ページの直線(OA’)は、3ページのy1に相当する。 (白夜に対応-4月23日に相当)
―> α=25.816°の線はx1軸に相当する
7/10ページの直線(OA’')は、同様に
―> α=-25.816°の線はx1軸に相当する。(極夜に対応-2月25日に相当)
以下の説明で、明確になります。



上図の4月18日の時点で、緯度80°の点は全て、白夜になっています。また地球の公転周期は365.25日ですから、1年に1/4日分ほどずれますから、閏年の前などは3/4日違っています。それは、基準となる春分の日の差になってきます。地球は約26,000年周期で歳差運動をしていますが、これは、春分点がごく僅かづつ、公転軌道上で移動していくことなので、白夜や極夜の日付けへの影響は無いのです。実際にはwikipediaによれば、北緯78°のsvalbard諸島では白夜は、4月20日に始まり、8月22日に終わるとなっています。これは私が春分点を3月23日(実際は3月21日とすべき)と設定している(これを考慮すると、私の計算では、白夜は4月16日に始まり、8月25日に終わることになります)のと緯度を78°として、この方法で計算すると、4月22日に始まり、8月20日に終わることになります。この計算と実際の2日の差の中の0.5日は、光の屈折によるものです。角度でも0.5°です。また0.25日は太陽の大きさの影響で、角度で約0.25°です。日に直すと同じく0.25日となります。(地球の公転軌道の半径は約1億5千万km、太陽の直径は約140万km、地球の直径は、約12,750 kmです)他には、地球はほぼ回転楕円体であること、当該地の地形や、測定地点(svalbard諸島のどの地点か)が丁度緯度78°であったのか、等にもよります。緯度が2°低くなったために、白夜の期間は6日遅く始まり、5日早く終わりことになります。
合掌
南無阿弥陀仏 南無阿弥陀仏
追記
1.厳密に、数学的に解くのであれば、下図に示す、POWER(X,2)+POWER(Y,2)=POWER((2.3*POWER(10,4)),2)- - -の地球の公転軌道円)と
POWER((X+a*cosθ),2)/POWER(0.17365,2)+POWER((Y+a:sinθ-0.39269),2)/POWER(0.15925,2)=1の楕円とが接するときの θ の値を求めることですが、この解は非常に計算が面倒である。それよりも、このようにしても十分な精度の計算が出来る。何故かというと、地球の半径を1とすると、地球が太陽の周りを回る公転軌道の半径は2.3*POWER(10,4)となり、上の様に円周を直線と考えても良いからです。これらの円と楕円が接する厳密解は θ=25.817°であり0.001°だけ増加しているだけなのです。
また、ここでのφは、地球の自転角度ではなく、緯度80°の各点の位相角だと考えて下さい。地球の自転の位相角度と公転の位相角度とは、関数関係にあるから、θ=一定ならば、φも一定であるからです。φを各点の位相角と考えれば、θとφは関数関係にはなく、任意の角度を取り得るからです。

2. 以上は地球は等速で公転軌道を動くとして計算しましたが、実際は、下図の様に公転軌道は楕円ですから、また公転速度はケプラーの面積法則によって、等しい時間で、動径が描く面積は等しくなるように公転しますので、春分点は以下の様な点にあると考えられます。これ以上、現実に近い計算をするには、実際の楕円の公転軌道を使い、今年は、春分点が公転軌道のどこにあるかを決定し、公転速度もケプラーの面積法則を使う、厳密解をしなければならないかも知れません。
















