ガウスと言えば、自ら”黄金の定理”と自画自賛した「平方剰余の相互法則」に代表される整数論や”驚異の定理”と呼ばれた「ガウス曲率」に代表される曲面論(微分幾何学)。それに、ケレス惑星の発見を導いた「最小二乗法」に代表される本職の天文学に、「ガウス分布」へと繋がる測地学や確率論。
更に実験物理学者としてのガウスの地位を広く知らしめたウェーバーとの共同研究による電信機の発明(1833)による電磁気学など・・・ガウスの役割は非常に広範囲で多岐に渡り、今もなお大きな威力を持つものである。
「その4」ではガウスの楕円関数論を概略のみでしたが、以下、「数学のアイデア」(トード・ハッル著、山下純一訳)と「近世数学史談」(高木貞治著)及び「ガウスの算術幾何平均を巡って」(PDF版、西和田公正)を参考に、少し踏み込んで紹介します。
ガウスの楕円関数論
意外にも思えるが、ガウスの関数論となるとそれ程の影響を跡づけるものが見つかりそうもない。しかし、22歳(1799)の時の楕円関数論の発見も含め、非常に若い時から数多くの新しいアイデアを発芽させていた。
事実、友人シュマッハーへの手紙(1808)には”三角関係や対数関数などの<初等関数>には既に興味がなく、楕円関数などの初等関数には変換できない<超越関数>に大きな感心があります。この分野は未開なままですが、私は以前かなり頑張って研究を進めた事がありました。「整数論考究」にヒントを書いてた様に、これら大きな仕事をいつか発表するつもりでいます。多くの数学者たちは、この未開の新しい(超越)関数に立ち向かう事なく、只々恐れているようです・・・”
つまり、ガウスが”未開の領域”と呼んだものは、楕円の弧長の計算の際に出現する楕円積分(後の楕円関数)の事である。
「その4」でも述べたが、アーベルもヤコビもガウスの「整数論考究」をヒントにして楕円積分に取り組み、数学史上最も有名な研究闘争に突入する。
ただ、これにガウスが沈黙を守ってたという事実はとても残念で不可解でならないが、ガウスは非ユークリッド幾何学の時の大騒ぎの時も、同じく無関心を通し続けた。
ヤコビが楕円関数の「逆問題」で有名になるのは、ガウスの宿敵であるルジャンドルのお陰でもある。
この楕円関数論が日の目を浴びるには長い時間が掛かり過ぎる事になるが、ヤコビはあえてガウスとは接触を試みなかったようである。事実、ガウスの学位50周年を祝う式典に参加したヤコビは”ガウスは20年間も私や弟子のディリクレを無視し続けています。全く我々の仕事を無視するよう企んでいる様です”と露骨に不満を述べている。
一方で、アーベルの運命はもっと悲劇的なもので、彼の天才には貧困や孤独がつきまとった。アーベルは僅か21歳の時、当時は未解決何代だった”5次方程式が四則とルートのみでは解き得ない”事を証明したが、すぐには評価されないどころか、期待してたガウスから”証明になっとらん”と手厳しく突っぱねられる。
アーベルは更に代数関数論に関する”パリの論文”をパリアカデミーに送るが、審査委員長のコーシーによって無視される。これは、ガウスもコーシーも自らの研究に追われ、読む暇がなかったとされるが、これら天才青年の論文に目を通してた事が明らかになっている。
事実ガウスは、アーベルがクレレ誌に発表した「楕円関数研究」(1827)にては目を通したらしく、”1798年以来考察を続けてる楕円関数の研究成果を他のやるべき仕事に追われ、完成できずにいます。しかし、アーベル氏がエレガントで明晰な方法によって私に追いついてきました。故に私の予定の1/3は不要になった。
アーベル氏は1798年に私が辿った全く同じ道を歩んでますから、私と同じ結果になったとしても驚きません。でも全てがコピーみたいで(誤解を招かない為にも)この事は誰にも話したりはしません”と、言い訳がましくも聞こえなくもない。
因みにアーベルは、23歳のガウスが初めて楕円積分を∫dx/√(1−αx²)(1−βx²)という形(第一種楕円積分)に書いたのを知る由もないが、全く同じ表記を提示していた。完全な偶然の一致だが、実に不思議な事でもある。
しかしガウスは1832年にも、(双曲幾何学を発表した)ボヤイに対し非ユークリッド幾何学に対する自らの優先権を確認するような手紙を書いている。いずれの場合も”神の様な高み”から、その冷酷さによって他者の心を凍りつかせる様なガウスの行為は褒められたものではない。
算術幾何平均と楕円関数
ガウスは15歳(1791)の時すでに「算術幾何平均」(相加相乗平均)について実験を試みている。
「その4」で書いた様に、a₀=a,b₀=bから出発し、a₁=(a₀+b₀)/2を算術平均、b₁=√(a₀b₀)を幾何平均として、a₂,b₂,a₃,b₃、、、aₙ,bₙを次々と求める。この時、a=a₀>a₁>a₂>aₙ>・・・>bₙ>・・・>b₂>b₁>b₀=bとなり、かつlim[n→∞]aₙ=lim[n→∞]bₙとなる事が解る。
この共通の極限値を”aとbの算術幾何平均”と呼び、M(a,b)と書く。この簡単な性質として、①M(a,b)=M(b,a)②M(a,b)=M(a₁,b₂)=・・・M(aₙ,bₙ)③M(λa,λb)=λM(a,b)がある。
M(a,b)自体はルジャンドルの研究で知られてはいたが、15歳の少年は、幾つかの例を計算する事で、これらの法則に気づいたとされる。更に、M(a,b)=aM(1,b/a)=bM(a/b,1)となるので、a又はbを1とすれば、ずっと計算が楽になる。
特にガウスは、M(1,0.2)やM(1,0.6)やM(√2,1)について詳しく計算した。
例えば、M(1,0.2)では、a₀=1とb₀=0.2から始め、僅かn=4項目で、a₄=0.5208016381…、b₄=0.5208016380…とほぼ同じになる。
この様に、算術幾何平均を与える数列は非常に速く収束する事が分かる。
更に、1/M(1+x,1−x)=1+(1/2)²x+(1・3/2・4)⁴x²+(1・3・5/2・4・6)²x⁶+…という自ら試みた級数展開式で、これをyとした時、(x³−x)d²y/dx²+(3x²−1)dy/dx+xy=0という微分方程式が導ける事に気付いた。
ガウス少年はこの一般解を考察する事で、1/M(1+x,1−x)=∑[0,∞](1・3・5・・・(2n−1)/2・4・6・・・(2n))²x²ⁿ=(2/π)∫[0,θ]dφ/√(1−x²sin²φ)―⑴という(算術幾何平均と級数展開と楕円積分関数を繋ぐ)興味深い関係式を発見する。
因みに、(1)式の最初の等号ですが、これは、1/M(1+x,1−x)=1+c₂x²+c₄x⁴+…とおき、変数変換x=2t/(1+t²)を行うと、1/M(1+x,1−x)=1/M(1,√(1−x²))={2t/(1+t²)}{(1+t²)/M(1+t²,1−t²)}=2t/M(1+t²,1−t²)となる。ここで、両端の項の級数展開を比べると、{2t/(1+t²)}{1+(2t/(1+t²))²+(2t/(1+t²))⁴+…}=2t(1+c₂x²+c₄x⁴+…)を得る。
そこで、更に左辺を展開し、未定係数法に持ち込めば、規則性がハッキリし、cₙ={(2n−1)!!/(2n)!!}²となり、一般項の級数展開を求める事が出来る。
一方で、2番目の等式ですが、左辺の第3項の被積分関数をxで級数展開し、項別積分すれば第2項と一致するとあるが、アホな私には??である。
そこで、u=sinφとおき、du/dφ=cosφ=√(1−u²)を(1)式の右辺に代入すると、θ=π/2→u=1より、(2/π)∫[0,π/2]dφ/√(1−x²cos²φ)=(2/π)∫[0,1]du/√((1−u²)(1−x²u²))を得る。
この式は、xを定数(モジュラ)とする(今で言う)第一種楕円積分の(2/π)倍となってる事がわかる。
因みに、これと全く同じ結果が1818年に発表した天文学の論文の中で述べられてる。これはガウスが楕円関数について発表した唯一の印刷物でもある。
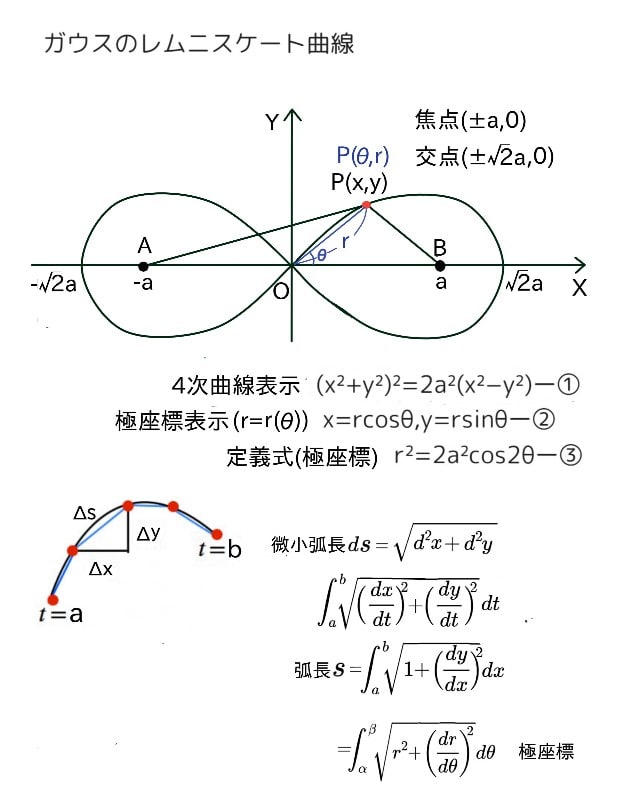
ガウスのレムニスケート曲線
「その4」でも書いた様に、19歳(1797)の冬にガウスは、レムニスケートの弧長に関する問題を起点にし、楕円関数の研究を始めます。
この曲線は、(x²+y²)²=2a²(x²−y²)ー①により定まる平面上(直交座標系)の4次曲線で、2つの焦点A(a,0)とB(−a,0)からの距離の積がa²となる曲線上の点P(x,y)の軌跡と言える。この時、曲線とx軸との2交点は(±√2a,0)となる(上図参照)。
但し、ループ1つで囲まれる面積もa²であり、OP間の曲線の弧長Sは(以下で説明する)楕円積分により表される。
一方で、曲線上の点P(x,y)を直交座標から極座標系のP(θ,r)に変換すれば、線分OPはr=r(θ)となり、x=rcosθ,y=rsinθー②とおける。これを①式に当てはめると、レムニスケートの(極座標での)定義式は、r²=2a²cos2θー③となる。
結論から言えば、原点から第一象限内(x,y≥0)にあるレムニスケート曲線上の点P(θ,r)までの弧長Sは(ガウスがした様に)2a²=1とすれば、S=∫[0,r]dr/√(1−r⁴)ー④で表せる。
一般に、y=f(x)のx=a~bの弧長はS=∫[a,b]√(1+f’(x)²)dxで表せる。
これは、ds=√(d²x+d²y)から、両辺を媒体変数tを使い、a~bの範囲で積分すれば、S=∫[a,b]√((dx/dt)²+(dy/dt)²)dtとなり、x=tとおけば、S=∫[a,b]√(1+(dy/dx)²)dxが得られる。dsという曲線上の微小距離の総和(積分)と考えれば、理解が早い(図参照)。
一方で、レムニスケート曲線(極座標表示)の時は、dx/dθ=drcosθ/dθ−r(θ)sinθ、dy/dθ=drsinθ/dθ+r(θ)cosθとなり、(dx/dθ)²+(dy/dθ)²=r²+(dr/dθ)²と変形できる。故に、0~θまでの弧長積分は(上と同様にして)、S=∫[0,θ]√(r²+(dr/dθ)²)dθー⑤となる。
ここで、√(r²+(dr/dθ)²)dθ=√((rdθ)²+(dr)²)より(θ→rとおき)、S=∫[0,r]√(1+r²(dθ/dr)²)drと変形。定義式r²=cos2θからdθ/dr=sin2θ/rを代入すれば、S=∫[0,r]√{(sin²(2θ)+r²)/sin²(2θ)}dr=∫[0,r]dr/√(1−r⁴)と④式を得る。
因みに、⑤式に定義式:r²=2a²cos2θを代入すれば、S=√2a∫[0,θ]dθ√(cos2θ)=√2a∫[0,θ]dθ/(1−2sin²θ}の一般式⑥を得る。
ここで、t=tanθ(0≤θ≤4/π)とおくとdθ=(1−sinθ)dtとsinθ=t²/1+t²を得て、S=√2a∫[0,t]dt/√(1−t⁴)を得る。また、レムニスケートの全周の長さをLとすれば、L/4=√2a∫[0,4/π]dθ/(1−2sin²θ}=√2a∫[0,1]dt/√(1−t⁴)となる事がわかる。
更に⑥式で、cos2θ=cos²φとおけば、dθ=(cosφsinφ)dφ/√(1−cosφ)と1−2sin²θ=cosφを得て、S=a∫[0,φ]dφ/√(1−sin²φ/2}が導ける。故にφ=π/2の時、L/4=√2a∫[0,1]dt/√(1−t⁴)=a∫[0,π/2]dφ/√(1−sin²φ/2}を得る。
但し、上式の積分∫dφ/√(1−sin²φ/2}は、今では第一種積分表示と呼ぶF(μ,θ)=∫[0,θ]dφ/√(1−μ²sin²φ/2}で記されるが、μ=1/√2,θ=π/2とすれば、L/4=aF(1/√2,π/2)と記せる。
次回でも述べるが、ガウスはa=1/√2として上式の(L/4の長さの)弧長積分をωとおき、ω=∫[0,1]dx/√(1−x⁴)=(1/√2)∫[0,π/2]dφ/√(1−sin²φ/2)を導き、M(1,√2)=π/2ωなる事を発見する。
実際にはガウスはω=ω’/2と記し、これはω’=2ωがレムニスケートの周期がπになる事を示す。但し、円では2πが周期になる事に注意です。
長くなったので、今日はここまでです。
次回は、楕円関数論におけるガウスの実験的手法について述べたいと思います。











楕円関数論に関しては、ガウス自身も相当に混乱したらしく、日記にはその軌跡も垣間見れるらしいです。
アーベルの論文を、約30年の歳月を経て”エレガント”と評した辺りは、ガウスの無念も含まれてるように思えます。
ガウスの数学は帰納的手法にその本性があるとされますが、楕円関数(積分)という超越関数をレムニスケートの等分理論を通じ、算術幾何平均という級数論に帰着させ、更にはモジュラー関数論に発展させる辺りは、驚異であり、他の数学者達には脅威に映った筈です。
PDFを少し読みましたが
曲線上の点Pと2定点A,Bの距離をr₁,r₂とすると、r₁+r₂=定数の時は楕円で、r₁−r₂=定数の時は双曲線で、r₁/r₂=定数の時は円(または直線)で、r₁r₂=定数(a²)の時はレムニスケートとの所が興味深くもありました。
言われる通り、級数展開を用いて導くんですが、凡人にはとても付いていけないレヴェルでした。
証明の概略だけは、次の記事で紹介するつもりですが、その雰囲気だけは何とか感じ取る事は出来たでしょうか。
”特殊から一般化へ”
これこそがガウスの口癖ですが、楕円関数を級数展開を用いて一般化し、更にモジュラ関数に昇華させるガウス流の帰納法にはホント頭が下がりますね。
今日のpaulさんのコメントにも脱帽ですよ。
ありがとうございます。