バベッジは暗号の上に卵を産む〜暗号の仕組み”その５”

　前回｢その4｣はRSA暗号の仕組みと起源について詳しく述べましたが､今回は少し寄り道して､エニグマやRSA暗号以前の暗号について紹介します。
　まずは暗号の前に､数表と計算機のお話からです。

　4000年前の古代エジプトに始まる三角法の歴史は､三角関数表作成と共に発展した。
　古代ギリシャのプトレマイオス(83-168)､15世紀ドイツの天文学者レギオモンタヌス(1436-1476)､16世紀オーストリアの天文学者ゲオルク･レティクス(1514-1574)らが脈々と三角関数表を作り上げてきた。
 日本で最初の三角関数表は､江戸時代の数学者建部賢弘(1664-1739)により導入･作成され､以降､天文学と航海術における三角関数表は時代を追う毎にその精度が高くなっていく。そして､三角関数の計算克服の為に誕生したのがネイピアによる対数表だった。
　つまり､”対数は天文学者の寿命を2倍にした”のである。

　つまり､人は死して数表を遺してきた。それら数表のお陰で､後世の人々は計算の為の時間を節約する事が出来たのだ。
　だが､数表の精度が高くなり､ミスのない数表を作る事の困難さが新たに大きな問題を引き起こす。理由は単純で､全てが手計算だったからだ。
 当時は計算道具といっても､18世紀ヨーロッパでは､ネイピアの計算棒(99表を印字した棒)や算盤だけだった。因みに､”computer”とは元々”計算する者”という意味だが､そのコンピュータ氏が計算したものを印刷工が活字を組んで印刷する事で数表は作成される。が､その全てのプロセスでミスが生まれる。
 1812年､1人の数学者が間違いだらけの対数表を眺めながら奇想天外なアイデアを思いつく。”そうだ。数表作成を全て機械にやらせよう”そう呟いた男こそが､今日紹介するチャールズ･バベッジ(1791-1871)だったのだ。

バベッジの計算機と暗号解読

 ネイピアが20年を費やして対数表を完成させたのが1614年。彼が発見した対数のお陰で数学のみならず自然科学は大きく発展する。中でも最大の革命は微分積分法であった。
　裕福な資産家の家に生まれたバベッジは、1810年にケンブリッジ大学トリニティカレッジに入学。学生時代はケンブリッジ大学に浸透するニュートン流微分積分法に反発し､合理的なライプニッツ流を推進し始める為に仲間と解析協会を設立する程で､バベッジは37歳の若さでニュートンが座っていたルーカス教授職に就く事になる。

 1812年､20歳を過ぎたばかりの青年バベッジの頭脳に浮かんだアイデアこそが数表自動作成マシンだった。
　人類で初めてプログラム可能な解析計算機(アナリティカル･エンジン)を考案したバベッジだが､コンピュータサイエンスの分野ではよく知られた偉人であり､チューリングと並んで”コンピュータの父”とも呼ばれる。
　そこで今日は、チャールズ･バベッジの数ある功績の一つである､ヴィジュネル暗号の解読について説明します。

　計算機科学者や哲学者でもあるバベッジは､階差機関(ディファレンス･エンジン)と呼ぶ階差数列を利用した､数表を次々と計算する機械を開発した。その後､その発展型である解析マシンの開発研究も行い､世界で初めてプログラムができる計算機を考案した人物と言える。
　彼が考案した計算機は､当時の主要エンジンだった蒸気機関が動力源であり､極めて実用性が高く､暗号解読には欠かせないものだったとされる。
　以下､｢チャールズ･バベッジとは・・｣より大まかに纏めます。

　GPSがなかった当時､航海をするには､三角関数表などを使って星の測量をし､自分の位置を手計算していた。故に､数が大きくなる程に正確な数表を作る事が困難になる。こうした精度が落ち､間違いだらけの数表を見たバベッジは､数表を自動的に計算し､印刷する機械を作ろうと考えた。
　そこで試作されたものが階差数列を利用し､数表を次々と計算する機械(階差機関=ディファレンスエンジン)である。その発展型の解析機関(アナリティカルエンジン)は､パンチカードでプログラムを組む機械で､プログラムをカードを機械に入れ交換する事で､様々な数表の印刷が実行できるとした。
　こうした機械をバベッジは亡くなる直前まで研究し､その後､彼のアイデアはエイダ･ラブレスにより実際に作成され､故にラブレスは”世界初のプログラマー”と呼ばれる。

　一方でバベッジは当時､計算機開発だけでなく､暗号解読も研究し､当時”解読不能”とされた”ヴィジュネル暗号”の攻略法を開発する。
　ヴィジュネル暗号とは､フランス外交官ブレーズ･ド･ヴィジュネル(1523-1596)により完成された”多表式の換字式暗号”の事で､”単一換字式暗号が安全ではない”と指摘される様になった15世紀後半〜16世紀後半と､約100年かけて考案された暗号だ。
　元々ヴィジュネル暗号は､ヴィジュネルが考案した訳でなく､まず1460年頃にレオン･バッティスタ･アルベルティが”多表式”の原型を思いつく。それまでの”換字式暗号”は1つの暗号アルファベットを使ってたが､2つ以上のアルファベットを使う事を考案した。
　これを引き継いだのが､ドイツの修道院長ヨハネス･トリテミウスで､アルベルティによる多表式の原型の研究を引き継ぎ､その後､イタリアの科学者ジョヴァンニ･ポルタが継承し､最終的にヴィジュネルが暗号を形として完成させた。　
　

換字式暗号とは？

　”換字式暗号”とは､アルファベットの文字を別の文字に置き換える事で暗号化したもので､”単一換字式暗号”と呼ばれる事もある。換字式暗号の中でも最も単純なものに､それぞれの文字を(a→xの様に)3文字前の文字に置き換える”シーザー暗号”がある。シーザー(カエサル)暗号に関しては｢番外編｣でも詳しく紹介しましたが､興味ある人は参考にして下さい。

　因みに､単一換字式暗号とは､平文の文字に対し､必ず同じ暗号文の文字に変換される暗号の事で､換字式暗号の中では単純なアルゴリズムとなる。例えば､平文の”a”が暗号文の”c”に 必ず 暗号化されれば､それは単一換字式暗号となる。
　一方で､古代ローマ皇帝シーザーも実際に使ってたとされ､単一換字式暗号で広く知られていた(上述の)”シーザー暗号”だが､アルゴリズムが単純な為に､紙とペンだけでも時間さえあれば解読出来る暗号文である。事実､平文が“hello”の時は､暗号文は“khoor”になるが解読は簡単だ。
　故に､この暗号では､使用される文字の種類(アルファベット文字26個−1の25個)しか鍵空間を確保できない事が強度の面で大きな問題点となっていた(上図)。その後､時代が進むにつれ､少し複雑な暗号が使われる様になる。
　その暗号こそが､単純なシーザー暗号より遥かに大きな鍵空間(データ長)を確保できる､変換リストを利用した”単一換字暗号”である。

　この単一換字暗号であれば､アルファベット26文字のみが対象だとしても26×25×24×23×22…3×2×1=4000兆の1兆倍もの鍵空間を確保できる事になる(上図)。
　つまり､これだけの鍵空間を確保できれば､解読はシーザー暗号よりも遥かに困難な事が判る。但し､鍵空間が大きくても暗号化アルゴリズムに明確な弱点が存在する単一換字式は安全とは言えない。つまり､どの文字がどの文字に暗号化されるかが決まってるからだ。
　そうした弱点により､解読には暗号鍵の”総当たり攻撃”よりも”頻度分析”が有効となる。故に､暗号文は長ければ長いほど解読には有利となる。

　また､時代が中世に進むと､頻度分析を用いた解読法により､変換リストを用いた単一換字式暗号も安全ではなくなる。従って､”多表式”の変換リストに加え､暗号鍵の文字列を用いる”ヴィジュネル暗号”や､単一換字式暗号の弱点を克服する為に平文の同じ文字が出現個所によって異なる文字に暗号化する新たな”換字式暗号”も開発されていく。
　そして､時代と共に換字式暗号も解読が進み､近代になると”エニグマ”に代表される”機械式”の換字式暗号や､プログラム可能な電子計算機による”電子式暗号”の時代に突入していく。それに加え､換字式の様な単純な暗号解読には言語学者が担当してたが､暗号が高度に複雑になると数学者の登用を促し､チューリングみたいな暗号解読の天才らを生む事になる。

ヴィジュネル暗号の仕組みと解読方法

　ヴィジュネル暗号とは､”ヴィジュネル方陣”と呼ぶ表を元に”換字表”を作る暗号方式である。
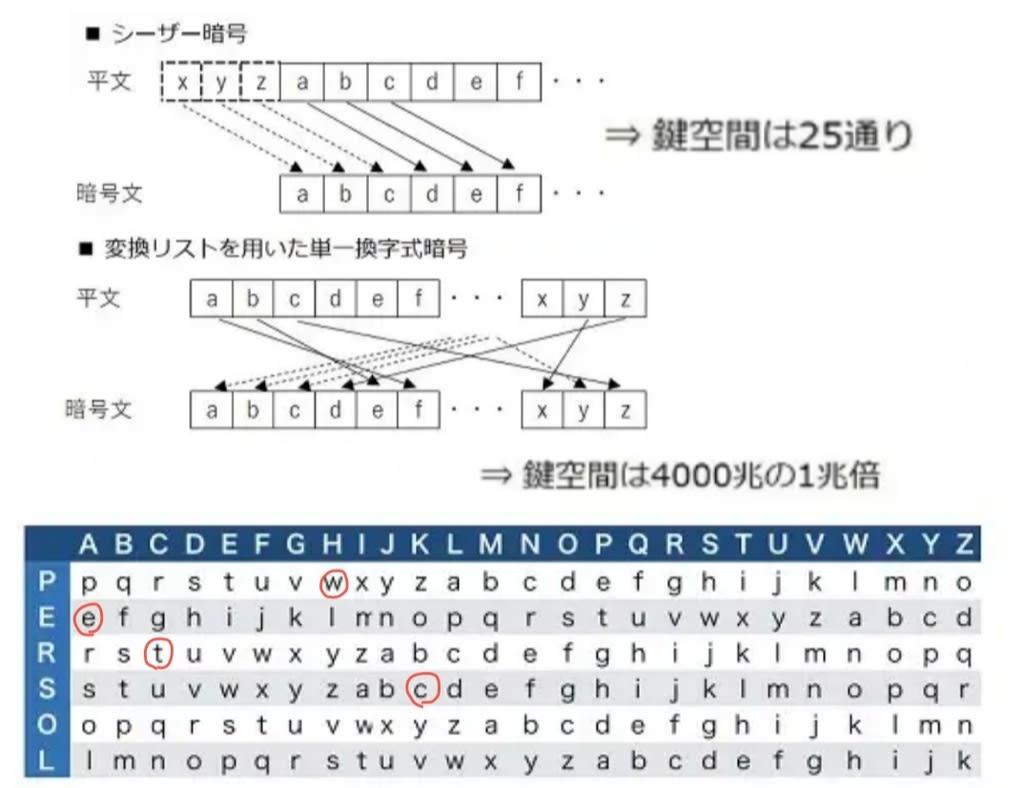
　これは図の様に､縦軸にA〜Z､横軸にもA〜Zのマスを用意し､1行目にa〜zの26個の文字を､2行目には1つずらし､b〜aの26個の文字を､26行目にはz〜yの文字を並べ､26×26個のマスを埋める。この表は単純で簡単に作れる為に､送受信者間で受け渡しをする必要がない。
　そこでまず”鍵語”を決める。文字数に制限はなく､長いほど暗号強度は高くなるが､暗号化と復号化の手間が掛かるのが欠点でもある。例えば､6文字の”PERSOL”を鍵語とする。ここで､ヴィジュネル方陣から”PERSOL”の6行を抜き出し､6×26の換字表(暗号表)を作る。原文の1文字目は”P”の行を使って暗号化し､2文字目は”E”の行を使って暗号化､7文字目は再び”P”の行に戻って暗号化を繰り返す(上図下参照)。
　復号化は､換字表を逆に見ていけば原文が現れる。事実､原文を”hack”とすれば暗号文は(赤丸で囲んだ文字列の)”wetc”となり､換字表を逆に辿れば原文の”hack”が現れる。

　ヴィジュネル暗号のメリットは､送信者と受信者の間で鍵語や換字表のやりとりがなくても済む点で､両者が同じ本を持ち､例えば送信日が7/23であれば”23ページの7番目の単語を鍵語にする”と定めるだけで換字表が決まり､暗号化と復号化のやりとりが完了する。
　もう1のメリットは”頻度分析に強い”事にある。英文の場合､出現する頻度が多い文字は”e”で､その次にt→a→o→i→n→…と続く事が判っている。故に､単純な換字暗号では､”e”は必ず別の同じ文字に置き換えられる為､暗号文に”e”が頻出する。
　従って､暗号文にある文字の出現回数を数え､”一番多い文字はe”と推測出来る。更に､他の文字の出現頻度も絡ませ､クロスワードパズルの要領で暗号を解読する事が可能となる。
　一方ヴィジュネル暗号では､同じ文字が続いたとしても､全く別の文字に置き換えられる為､頻度分析が使えない。また鍵語を長くすれば､暗号文のどの文字もほぼ同じ割合で出現する為に”解読不能”とされてきた。

　しかしバベッジは､このヴィジュネル暗号の攻略法として､同じ文字列が繰り返し登場する”周期性”に注目した。　　
　例えば､鍵語”PERSOL”を使い､同様に”hack”との文字列が繰り返す原文を暗号化する。ここで”hack”は､色んな文字列に変換されるが､6文字の鍵語と4文字の原文がシンクロ(同期)し､全く同じ文字列に変換される事がある。これは､鍵語の同じ部分で暗号化されてるからだ。
　事実､”hackhackhackhack…”の原文でみれば､暗号文は”wetcvlroysqvwetc…”となり､w~wまでの12文字の距離(循環列)が見つかるので､鍵語の文字数は12,6,3,2,1のいずれかと推測できる。

ヴィジュネル暗号攻略とクリブ攻撃

　この法則を見つけたバベッジは､暗号文の中に同じ文字列が出現する時､同じ単語がうまく鍵語と同期し､暗号文が復号された可能性があると考えた。更に､同じ文字列の間の距離(循環文字数)は､鍵語の文字数の倍数になる事にも気づいた。
　こうした同じ文字列の距離を数えて統計を取り､その距離の最大公約数が鍵語の長さになると推測し､鍵語の長さが例えば6文字だと分かれば､暗号文の6文字毎の文字頻度を数えれば､一番多いのが”e”であるとの推測が可能になる。
　単純な換字暗号から比べれば､ヴィジュネル暗号解読には大きな労力が掛かるが､外交電文や軍用電文などは､それだけ手間が掛かっても解読する価値と需要があるのだ。

　上記の性質を利用し､暗号文から同じ文字列の距離を数える攻略法は”カシスキーテスト”と呼ばれる。
　これは､繰り返し登場する同じ文字列の距離を数える暗号解読の手法の事で､6文字,2文字,3文字,12文字置きに同じ文字列が登場する事が多く､鍵語の文字数はこの様な数の公約数である可能性が高い。この名称は､10年後に暗号解読者フリードリッヒ･カシスキー(独)が独自に発見･公表した結果に基づいて付けられた。
　一方で､バベッジ自身はこの手法を発見していたが､公表はしなかった。本人は大した発見だとは思ってなかったし､英国陸軍が非公表にする事を命じたからだとも言われている。

　また､”クリブ”という着眼点から鍵語を推測する事も可能である。暗号解読におけるクリブ(crib) とは､既知の又は想定されうる平文サンプルの事で､第2次世界大戦中に英国の暗号解読作戦の本拠地ブレッチリーパークにて､この言葉が使われ始めた。
　例えば､難解で不可解に思える暗号文でも､元となる平文中の数語から既知又は想定可能なフレーズが見つかれば､解読の糸口を掴む事ができる。また総当たり攻撃の場合でも､復号した文中にクリブが見つかれば､試みた復号方法が正しいと推測でき､全文の解読に繋がるという。

　一方で､暗号文の種類によっては､原文に使われそうな単語を推測できる事がある。例えば､軍用電文では”ロンドン”や”パリ”や”リバプール”といった地名､それに”快晴”や”濃霧”といった気象用語がよく使われる。
　そこで､Londonであれば､暗号文の1文字目から６文字目までがLondonだと仮定し､ヴィジュネル方陣を逆算し､鍵語を推測する。鍵語は意味のある単語が使われる事が多く､推測した鍵語がデタラメな文字列であれば攻略は失敗となる。次に2~7文字目までがLondonと仮定し､以降は同じ事を繰り返す。
　もし､原文の何処かにLondonが使われていれば､意味の通じる鍵語が現れる筈だ。
　こうして､次々とヴィジュネル暗号の攻略法が開発されていくが､中でも有力なのが”クリブ攻撃”である。
　勿論､暗号を使う側も様々な対策をし､ヴィジュネル暗号も進化する。例えば､頻出する単語LondonやLiverpoolは､LDNやLVPなどという略号にするのが､軍用電文では基本中の基本になる。

ヴィジュネル暗号からエニグマへ

　暗号技術の大きな転換点は､1925年にドイツ軍に採用されたエニグマ暗号機だ。アルファベット26文字分の歯がついた歯車3枚によって暗号化され､3枚の歯車はリムーバブル方式になり､暗号機にセットする順番も変える事が出来る。つまり､(3×2×1)×(26×26×26)＝10万5456通りの変換方法が可能となる。
　原理はヴィジュネル暗号と根本は同じだが､鍵語の長さが10万5456文字になる為､カシスキーテストは通用しない。
　エニグマ暗号も､当時のドイツ軍は”解読不能”と謳い､敵の前線の弱点に爆撃機と戦車を1点集中させる電撃作戦や､敵輸送船団にUボートを1点集中させて攻撃する群狼作戦が可能になったのも､エニグマ暗号により前線部隊同士で安全に通信ができ､密な連携が可能になったからだ。また､ドイツ軍は電子式の暗号機を開発し､ビット演算をするローレンツ暗号を使い始め､連合国を翻弄する。

　ポーランドの暗号解読者マリヤン･レイエフスキーは､バベッジのアイディアとは異なるが､エニグマ暗号の周期性を探り､それを基に解読を試み､その周期性を発見する為の”ボンブ”と呼ぶ機械までも開発していた。
　イギリスの暗号解読拠点”ブレッチリーパーク”で暗号解読の仕事をしてた数学者のアラン･チューリングは､エニグマ暗号をクリブ攻撃の手法で解読する為に､電子式ボンブを開発した。更に､同拠点のトミー･フラワーズは､ローレンツ暗号にクリブ攻撃をする為に､電子式の解読機械”コロッサス”を開発。
　このコロッサスこそが､世界初の電子計算機であるとの説もある。

　一方で､ヴィジュネル暗号も”自己鍵式”と呼ぶものが考案され､これは原文の先頭部分は”PERSOL”などの定められた鍵語で暗号化するが､それ以降は原文の文字列を鍵語に使って暗号化する。
　受信者は､定められた鍵語で暗号文の解読を始めると原文が現れ､以降はそれを鍵として解読していけば良いが､一般のヴィジュネル暗号の様な周期性は稀にしか現れないので､カシスキーテストが通用しない。
　例えば､”Alicewasbiginning…”との原文を鍵語”PERSOLALICEWASBIGINN…”で暗号化すれば､”ppzushpdjgkenfjrm…”を得る。復号化する時は､まず定められた鍵語”PERSOL”で解読し､原文”alicew”が現れるので､”asbiginning…”を以降の鍵として復号化を進めていく。
　事実､同様の暗号強度を増すテクニックは､エニグマ暗号でも使われた。

　以上を振り返ると､バベッジが紙と鉛筆と思索で解読した暗号は､第2次世界大戦中に機械式に､そして電子式に急速に進化する。また､コロッサス以降､電子計算機も急速に進化&発展し､現在私たちが使うコンピュータやスマホに繋がっている。
　今や､SSLやRSAといった暗号技術はネットショッピングやオンラインバンキングを行うには欠かせないないものとなり､バベッジの時代から200年程が経つが､暗号技術は常に進化を続けている。
　以上､パーソル･クロステクノロジーから長々とでした。

最後に〜RSA暗号システムの限界

　RSA暗号とは､公開鍵暗号アルゴリズムの1つで､ネット上での電子署名(SSL証明書)として普及し､SSL(Secure Sockets Layer)証明書には､RSAがドメイン認証を行う為に広く利用される。
　因みに”ドメイン認証”とは､アクセス先のドメイン(住所)がブラウザのアドレスバーに表示されるドメインと一致してる事を確認する”なりすまし防止”の為の重要な認証となる。一方､この認証は電子署名によって支えられ､SSL証明書は認証局が申請者に対し､認証確認を電子署名により行うが､ここでRSAが使われる。

　事実､SSLを導入するとURLがhttpから”https”に変更される。但し､末尾の”s”はsecure(安全)の頭文字である。
　この”https”は､封筒に入った手紙の様なもので､封筒を開けない限り中身を読む事ができず､個人情報の流出を回避する。しかし現在は､TLS(Transport Layer Security)がSSLに代わり､より強力な暗号化技術を採用し､データ認証と暗号化方法が大きく改善されてるが､通常はSSLと呼ばれる。
　つまり､RSA暗号システムの堅固性がSSLを支えてると言える。

　そこで､RSAは解読できるのか？という重要な問題が浮上する。結論から言えば､現実的には不可能だが､それには理由がある。
　年単位の時間をかければ､RSAの2048bitの長さの鍵語を総当りで計算すれば解読できる可能性はあるが､数分で解読する事は現在のコンピュータでは不可能だ。
　仮に量子コンピュータが実用化された場合､RSAは脆弱になるとされるが､それでも現実的な早さで解読できるには至らない。

　一方で､現在の一般的なRSAの鍵長は2048bitだが､何故2048bitなのか？
　実は､暗号アルゴリズムの最適な鍵長は”コンピュータの性能がムーアの法則に従って進化する”という前提で決められる。つまり､ある日突然に数十年分程の一気に進化した高性能なコンピュータが発明されるか､RSAを高速で解読できるプログラムが開発されるかしない限り､RSA暗号を現実的な早さで解読する事は不可能とされる。
　もし､それらが本当に実現すれば､RSAは脆弱になる。今回､SNS上で話題になったのは､後者の”高速で解読できる理論”と言える。

　殆どのサーバでは秘密鍵を生成する際､2048bitの鍵長を選択するが､この鍵長(暗号鍵のデータ長)はパスワードの長さと同じく､長い程に暗号強度は上がるが､パスワードと違うのは､データを復号する時も鍵長が長いほど復号に時間が掛かる。つまり､鍵長が長い程に暗号強度は上がるが､利便性は下がる。
　現在､様々な暗号アルゴリズムで秘密鍵や共通鍵との鍵が使われてるが､アルゴリズム毎に”適した鍵長”は異なる。
　これは”等価安全性”と呼ばれ､暗号アルゴリズム毎に2030年までは2048bit､2050年までは3072bitと言う風に年代別で決められている。つまり､鍵長が長いほど安全だが､復号時の負荷などを考え､2030年までの技術であれば2048bitでも”リスクは低い”という風に､コンピュータ技術の進化を計算に入れ､決められている。その結果､RSAの鍵長は2048bitが現在の主流となるのだ。

　そこで万が一､RSAが解読されれば､ドメイン認証(SSL証明)は無効になり､現在SSL証明書による暗号化通信は金融機関やECサイトでほぼ100％利用されてるから､事実上のインターネット崩壊となる。
　勿論､ドメイン認証はRSA以外にも存在するが､”ポストRSA”とされる楕円曲線暗号(ECC)以外は中々普及が進まない。更に､PCやスマホに導入されてるルート証明はRSAに依存してる為に､頭が痛い問題でもある。
　勿論､RSAが突破される事は､現実的にはレアなケースではあるが・・・

　以上､長々とですが､RSA以前の暗号の歴史と仕組みについて紹介しました。ただ書いてる内容はそれほど難解ではなく､スラスラと読めるレヴェルなので､現代の暗号理論を理解する下準備としても有効だと思います。