頭の体操・その７：発想力が問われる算数の解答

ブログ人気投票にクリックいただけると幸いです！


　今日のブログは、昨日出題した下記の算数問題の解答だけ載せます。

マッキーの頭の体操・その７：発想力が問われる算数

　昨日、出題の算数の問題、解けたでしょうか？毎日多くの方が、私のブログをご覧になっています。その中で、この問題に取り組み、中学数学の「三平方の定理」を使わず、小学生に指導できる解答を導き出した人は、どれだけいたでしょうか。念の為に、再度問題を載せておきます。

　円の中に、下の図のように５つの正方形でできた図形が内接しています。円の直径は１０ｃｍです。では、この図の一つの正方形の面積は、何平方センチメートルでしょう。（もちろん、内接という言葉は、小学生は使いません。私が覚えている問題の設定を、設問にしただけです。）



　この問題を、三平方の定理を使って解くと、簡単に解答できます。まず、その解き方から示してみたいと思います。

　正方形の一辺の長さを１とすると、正方形が３つ続きの長方形の他の１辺の長さは、３と置くことができます。すると三平方の定理から、この長方形の対角線である斜辺の長さは、１×１+３×３＝１０、よってルート１０となります。この対角線が、唯一数値として出ている、円の直径１０ｃｍとなっていますので、１０ｃｍをルート１０で割って、１に当たる数、すなわち一つの正方形の一辺の長さを、ルート１０ｃｍと求めることができます。

したがって、一つの正方形の面積は、ルート１０×ルート１０＝１０（平方センチメートル）

　話は少しずれますが、中学生になっても、１０ｃｍの割合がルート１０の時、１に当たる数、すなわちもとにする量を求めることができない生徒が多いのに、驚かされます。例えば１０ｃｍの割合が２の時、もとにする量（その割合は１）は、１０÷２＝５となることは、経験的に理解できますので、間違える生徒はほとんどいないでしょう。しかし、割合が分数や少数、または今回のように無理数となると、その単純な経験では、解くことができません。整数から発展させて考えることができないのです。これは、小学校算数の学習の不備と言えます。この点に関して、私のブログで繰り返し考察していますので、時間があったらご覧ください。


　では、この問題を、小学生に指導する方法で解いてみたいと思います。熟慮の末、この方法を見つけても、その人は指導のプロとは言えません。入試の制限時間は、およそ５分でしょう。その範囲内で、小学生の解き方を見つけた人のみ、正解とします。

　まず、与えられた円の直径１０ｃｍから、導き出される数値を考えます。・・・円周の長さ、円の面積、それから？・・・これらが、この問題の解答に連動しないことは、すぐに分かります。そこで次に考えることは、この直径が３つの正方形がつながった長方形の対角線になっていることは、先ほど示した通り、考えつく方は多いでしょう。しかし、ここから三平方は使えません。

この直径を活用した図形は、他にあるかどうか考えてみます。すると、下の図のように、頂点を一つおきに結んでいくと、円に内接する一つの大きな正方形が出来上がり、その正方形の対角線が円の直径となっていることに気づきます。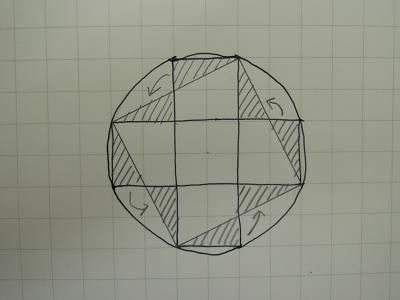



　正方形の面積を求める公式は、１辺×１辺ですが、正方形はひし形の仲間ですので、対角線×対角線÷２でも、求めることができます。対角線の長さが、円の直径１０ｃｍとなっていますので、この大きな正方形の面積は、１０×１０÷２＝５０（平方センチメートル）であることが分かります。

　元の小さな正方形５つでできた図形と、この大きな正方形を重ねて考えます。すると、大きな正方形から飛び出した直角三角形４つ（斜線部分）は、中の欠けている直角三角形４つ（斜線部分）と合同になっていることが分かります。そこで、上の図のように飛び出した三角形を、欠けている三角形の部分に等積移動します。その結果、大きな一つの正方形と、小さな５つの正方形が組み合わさった元の図形の面積が、一致することが分かります。

　よって求める小さな正方形１つ分の面積は、１０×１０÷２＝５０（大きな正方形の面積＝元の５つの小さな正方形が組み合わさった図形の面積）。よって、求める小さな正方形の面積は、５０÷５＝１０（平方センチメートル）となります。ちょっとした工夫ができれば、中３で学習する三平方を使うよりも、簡単に答えを出すことができます。

　円の直径１０ｃｍをどう使うのかを考え、それが円に内接する正方形の対角線となっていることに気づくこと。そして、その大きな正方形が、小さな正方形５つでできた図形の面積と等しいことを見抜くこと。基礎的な知識を活用するための、ちょっとした発想力を必要とする問題です。