ブログ人気投票にクリックいただけると幸いです！
未知なものに対する探求心は、新たな知識を獲得する喜びを原動力としていると思います。
それは、大人は無論のこと、子どもにとっても大切なことで、学習を指導する場合、常にその点に留意して指導することが大切です。
最近、ある小学校の小６の授業で、小５の終わりに習った円に関する問題について復習するために、まず公式を生徒に聞いてみました。
すると、過半数を超える生徒が、すでにその公式を忘れていることが判りました。
円に関する問題、例えば円周の長さ・円の面積・おうぎ形のまわりの長さや面積などを復習する時、求積公式を覚えているか、確認する必要があります。
公式を覚えることが、無味乾燥な学習と思われがちですが、はたしてそうでしょうか。
算数・数学は論理的に考える教科ということで、覚えることを軽視（忌避）し、公式の定着度が弱い場合、その公式を使って問題を考える喜びさえ知らずに、意図せず算数嫌いを増殖させることにもなります。
この事実は、求積公式だけではなく、割合や速さの公式にも当てはまります。
「あのね、割合の公式・速さの公式なんか覚えちゃダメなんだよ」などと、変に馴れなれしいタイトルで、公式不要論をブログで展開している塾教師もいます。
しかし、公式を教えずに割合や速さを教えるという趣旨を活かす対応策が不十分で、生徒が興味を持って公式を学習するために必要な指導力が無い結果、そのような主張をしているように、私には思われます。
公立中学校で中３に対し、同様に円に絡む長さや面積の問題を出すと、予想以上にその公式を忘れている生徒が多いのに驚かされるという事実からすれば、小６が小５で習った公式を忘れていても致し方ないと感じました。
小６の授業では、求積問題をやる前に、まず私はおよそ以下のような話からスタートして、公式の持つ意義と重要性を理解してもらうよう指導しました。
（アベリア）
「紀元前２０００年頃、古代バビロニアでは、円周の長さが直径の（３＋１／７）倍であることは知られていました。
また、紀元前１７００年から１８００年頃には、古代エジプトにおいて円の面積を求める方法も考案されていました。
大河の河口に古代文明は発生しましたが、その河口は肥沃な土地に恵まれました。
それは、毎年川が氾濫し、上流から養分を含む土砂を運搬し堆積させてきたからです。
反面、川の氾濫のために、所有する土地の境界線が不明瞭となることもしばしばだったでしょう。
その結果、それらの地域では、境界線を確定するために、測量技術や数学が発達したといわれています。
紀元前３世紀、古代ギリシャの数学者であり、さまざまな分野においてたぐいまれな才能を発揮したアルキメデスは、円周率の概数が３．１４であることを示しました。
このように人間の長い歴史の中で、多くの人たちの努力の成果として、君たちが習っている円周の長さを求める式や、円の面積を求める式が生み出されました。
多くの人たちの涙ぐましい努力を無にすることなく、人類の貴重な知の資産を受け継ぎ、君たちはこのような公式をしっかりと覚えて使えるようにしなければなりません。」
（ネジバナ）
小６の授業で「円に関する問題」を復習した理由は、平面図形の面積を求める公式はすべて小学校課程で習い終わるので、「平面図形の公式を総チェック」をすること、円周率（３．１４）を使うので「小数計算のチェック」をすること、ちょっと複雑な円に関する問題は、「計算の工夫（分配の法則）」をすることにより、楽に計算ができるかどうかをチェックすることなど、これら３つの学力を試して復習できるからです。
ところで、平面図形の面積を求める公式は、その図形を書いてその公式が導き出された理由を説明できなければなりません。
公式が導き出される過程を脇に置いて、公式を丸暗記すれば良いのだという考えでは、算数・数学の力を高めることはできません。
しかし、円周の長さを求める式や、円の面積を求める公式は、説明が難しく丸暗記せざるを得ませんので、その公式がどの様な変遷を経て作り出されたのか、生徒が興味が持てるように周辺部を掘り下げて説明する必要があります。
（確かに、円の面積を求めるのに、円を半円に分けて細かく切れ目を入れて開き、それを合わせて長方形（平行四辺形）にしてしまい、公式を説明することは可能です。）
なかなか公式の成り立ちを説明できないという観点から、円に関する公式が、小中学生に忘れられ易いことは、残念ながら納得できます。
（トケイソウ）
『紀元前１７００年から１８００年頃には、古代エジプトにおいて円の面積を求める方法も考案されていました』と記述しましたが、最近のテレビでそのことを古代エジプトの人たちの暮らしとともに話題にした番組がありました。
古代エジプトのパピルスに記された、その当時の数学の問題として、円の面積を求める考え方が示されていたことも取り上げていました。
その公式とは、『円の面積＝（直径－直径×１/９）の２乗』という式で、円の直径からその１／９を引いた長さを一片とする正方形の面積と、求める円の面積が等しいとする公式です。
小学生に教える円の面積を求める公式は、『半径×半径×円周率（３．１４）』です。
私は、古代エジプトで考案された円の面積を求める公式が、実際はどの程度正確な面積を求められるのか知りたくなり、上の式を変形して、今小学生が使っている円の面積の公式と対応させてみました。
（直径－直径×１/９）の２乗
＝（直径×８／９）の２乗 （本来はこれを公式とすべきだと思います。）
＝（半径×２×８／９）の２乗 （直径に半径×２を代入）
＝半径×半径×１６／９×１６／９
＝半径×半径×２５６／８１
この式の変形は、理解いただけましたでしょうか？
この結果からすると、小学生が使う円周率３．１４と、上の式の２５６／８１が近ければ、かなり正確な円の面積を求める式であることが判ります。
そこで、比較のために分数を小数に直してみると、２５６／８１＝２５６÷８１＝３．１６０４９３８・・・と続く小数となりました。
（小学生には、小数第二位まで計算するように指示）
この数値を、３．１４１５９で割ると、１．００６０１７２・・・、計算ミスかと思って再度電卓を打ち直しましたが、やはりこの数値が出ます。（小学生には、３．１６を３．１４でわって小数第三位まで求めるように指示）
この結果から、およそ４０００年前の古代エジプトにおいて、現在知られている円周率を使う場合と、驚くことに０．６％の誤差で円の面積を求めていたことが判りました。
この計算過程を、江東区の南央小学校や第二大島小学校の小５や小６の生徒に、アドバイスを与えながらやってもらいました。
公立小学校では、小数どうしの除法は小５で、また分数どうしの乗除は小６で学習する内容ですので、出来る計算は限定されます。
しかし、自分のノートの上で、古代の人々が使った公式を、本当に正確な面積が出せるものなのかを助言を得ながら判定することは、生徒にとって興味深いことでした。
直径を１０ｃｍと仮に置き、古代と現在習っている公式に当てはめて、比較する方法もありますが、やはり公式自体の評価をすることのほうが、意味あることでしょう。
ある学校では、この私の授業を行った日が学校公開日で、生徒が黒板に書かれた古代エジブトの公式にチャレンジしている姿を参観しながら、一緒になって保護者も興味津々といった面持ちで聞き入っていました。
（八重のクチナシ）
ブログ人気投票にクリックいただけると幸いです！
下の「ゆずり葉」と題される詩は、河井酔茗（1874年～1965年）の詩です。先日、塾の小５国語の授業で、この詩をとりあげました。まずは、その詩をお読み下さい。
子供たちよ。
これはゆずり葉の木です。
このゆずり葉は
新しい葉が出来ると
入り代わってふるい葉が落ちてしまうのです。
こんなに厚い葉
こんなに大きい葉でも
新しい葉が出来ると無造作に落ちる
新しい葉にいのちをゆずって――。
子供たちよ
お前たちは何をほしがらないでも
すべてのものがお前たちにゆずられるのです。
太陽のめぐるかぎり
ゆずられるものは絶えません。
かがやける大都会も
そっくりお前たちがゆずり受けるのです。
読みきれないほどの書物も
みんなお前たちの手に受け取るのです。
幸福なる子供たちよ
お前たちの手はまだ小さいけれど――。
世のお父さん、お母さんたちは
何一つ持ってゆかない。
みんなお前たちにゆずってゆくために
いのちあるもの、よいもの、美しいものを、
一生懸命に造っています。
今、お前たちは気が付かないけれど
ひとりでにいのちは延びる。
鳥のようにうたい、花のように笑っている間に
気が付いてきます。
そしたら子供たちよ、
もう一度ゆずり葉の木の下に立って
ゆずり葉を見る時が来るでしょう。 
最近公園で見かけたユズリハの画像ですが、上に開いた葉が新しい葉で、下のシワが寄った葉が古い葉。
【ユズリハ】
ユズリハ科ユズリハ属の常緑高木で、古名はユズルハ。ユズリハの名は、春に枝先に若葉が出たあと、前年の葉がそれに譲るように落葉することから。その様子を、親が子を育てて家が代々続いていくように見立てて縁起物とされ、正月の飾りや庭木に使われる。
河井酔茗「ゆずり葉」というこの詩は、自分の子どもに対する慈愛に満ちた父親の心情がよく表された詩です。大人（親）が読んでも子供が読んでも耳に快い言葉が綴られています。しかし、ちょっと時代が異なると言えども、詩の内容が楽観的過ぎる印象を、私は受けます。大正時代、そして昭和初期に活躍したであろう、この詩人が生きた社会状況は、こんなに優しい心情を吐露できる時代背景だったのか、疑問を感じます。調べてみると、この「ゆずり葉」の詩は、『紫羅欄花』（1932年）に所収された一編であり、1932年は昭和7年にあたります。
この時期に起こったことを簡単に述べるなら、悪法の中の悪法である治安維持法により、さまざまな文化・思想が弾圧を受け、国家主義的な機運が高まった時代でした。昭和4年には、ニューヨークのウオール街での株価大暴落によって、世界大恐慌が引き起こされ、経済的にも厳しい世の中となり、ファシズムが台頭した時代となりました。狂気の世界の始まりでした。
この詩が発表される前年の昭和6年には、関東軍による柳条湖事件を契機とした満州事変が起き、日本は大陸侵略を本格化させました。（塾では小5で学習） まさに、社会が混乱し、軍部が台頭し、子女を含む多くの犠牲者を出した戦争への道を転げ落ちていくような時代背景だったはずです。こうした世の中の大人の行為を、ここまで美化できることが私には理解できません。
はたして、人類は子孫のために、ゆずり葉のように、『新しい葉が出来ると無造作に落ちる 新しい葉にいのちをゆずって――。』と、胸をはって言えるでしょうか。そしてこの詩人が語った、『みんなお前たちにゆずってゆくために いのちあるもの、よいもの、美しいものを、一生懸命に造っています。』と、そうした時代を賛美することができるでしょうか。私は、この時代背景を無視し肯定的に捉えているこの作家に、たいへん違和感を覚えます。
この時代の異常さを訴え行動したために、多くの人達が官憲により拷問され、牢獄から生きて帰りませんでした。文化活動も言論も厳しい統制を受け、逮捕された本人以外にもその家族は国賊として世間から理不尽な痛みを受けたのでした。イデオロギーを超えて、私たちの国の誤った行く末を案じて、多くの人達が命を懸けて行動した時代に、その時代や自分を含む大人たちの行いを賛美するこの詩に、私は憤りを覚えるのです。
では平和な時代の現代において、この詩は生きてくるのでしょうか。けれども、この作家が生きた戦争の時代とは異なりますが、地球温暖化・酸性雨・オゾンホール・ダイオキシン、膨大にふくれあがった国の借金、そしてまき散らされた放射性物質など、さまざまな深刻な問題が積み上げられれつつあります。
下手をすると、虹色に輝く宝物をゆずるのではなく、そうした重い負の遺産を子どもたちに背負わせることになりはしないか？愛おしい子供たちに残すべき自然環境・社会環境を考えると、この詩人のように、今の私たち大人の行いを肯定的にとらえた「ゆずり葉」の詩の言葉を、子どもたちに送ることができるかどうか疑問です。この詩のように、現在の私たち大人の行いを美しく飾るのではなく、もっと自省の念をもって深く考える必要があるはずです。
ただし、社会が悪い、国が悪いと愚痴をこぼしても、前進しません。また、我が子だけ良ければよいといった利己的な考えも困りものです。自分の出来るところから、少しずつ努力をしていくことが、私達大人の、子どもたちに対する責務と考えるべきです。
最後に付け加えれば、以上で述べた私の感想は授業では封印し、ユズリハという植物の生態を、子に対する親の情愛の比喩として書かれたこの詩について、一般的な鑑賞を指導しました。
ブログ人気投票にクリックいただけると幸いです！
今日の問題も、中学生から出た質問で、一般の大人でもちょっと工夫すれば解くことのできる、作図に関する問題です。
コンパスがなくとも、紙と鉛筆さえあれば、よほど不器用でなければ、手コンパス（コンパスを使ったつもり）で作図することができますし、今回の問題などはそれで充分です。
数学が得意だった方は、ヒントを見ないで解いてください。
さて、あなたは解答を導き出すまで、ヒントを見ない「こだわり派」か、結果を早く知りたい「せっかち派」でしょうか？
【問題】
下の図のように、正方形ABCDの中に、長方形PQRSが入っています。
正方形の面積を二等分し、かつ長方形の面積も二等分するような直線Lを、作図してください。
長方形PQRSの位置や大きさは、この問題を解くにあたり、関係ありません。
【ヒント】
問題文を読んで、即座にこの問題のポイントが読めた人は、数学的な素養のある人です。
ただ、この問題の考え方は、高校入試の関数などの問題に応用されていて、中学生は知っていることが必要です。
この問題を解くにあたり、下のような平行四辺形の面積を二等分する直線を引くことができるか、ここが解けるかどうかの分岐点となります。
「そりゃあ簡単だろう！」
「対角線ACまたは対角線BDで切れば、この平行四辺形を合同（同じ形で同じ大きさ）な三角形二つに分けることができるでしょう。」
無論、その通りですが、今回の問題を解くためには、この平行四辺形の内部の一点を通るように切れば、無限にそうした切り方があるということに気づくかどうかがポイントとなります。
正方形も長方形も、平行四辺形の仲間に入ります。
したがって、平行四辺形を二等分する考え方は、正方形にも長方形にも当てはまります。
下の図のように、対角線ACとBDを引き、その交点を点Oとします。
点Oを通るように引いた任意の直線Lや直線ｍにより、この平行四辺形の面積は二等分されます。
すなわち、下の図のように、合同な二つの台形に分けることができます。
数学が得意な人は、合同の証明をしてみてください。
【解答】
正方形の対角線ACとBDの交点Mを作図して求めます。
同様に、長方形の対角線PRとQSの交点Nを求めます。
その二つの交点MとNを通るように引いた直線Lは、ヒントで説明したとおり、正方形と長方形それぞれを、二等分する直線となります。
ブログ人気投票にクリックいただけると幸いです！
だいぶ遅れて咲き出した桜の下を通り、希望と不安を胸に、入学式に向かう子供たちの姿を見かける季節になりました。
特に中学受験や高校受験を経て、新しい学校に進学する生徒たちは、徒歩圏にあった近隣の学校で、顔見知りの仲間が集う今までの学校と比べ、多くの点で異なった環境の学園生活が待っています。
ただ、大人が考えている以上に、子供の新しい環境に対する適応能力は高く、父母の心配は杞憂に終わることが多いのも事実です。
それでも、環境が著しく変わるこうした子供と係わる大人たちは、子供の置かれている状況に対して関心を持ちつつ、暖かく見守っていく必要があります。
（早咲きの緋寒桜（寒緋桜）と、黄色い花はレンギョウ）
ところで、新高１になる教室の女子生徒が、春期講習に参加しているとき、これから通う高校の先生から、入学式に新入生代表として挨拶するようにと言われたと、困惑したような顔で、私に話しかけてきました。
原稿用紙で２～３枚程のスピーチをどうまとめるのか、そのアドバイスを求めてきたのです。
「まずは、代表挨拶を前向きな気持で引き受けること。それはとても名誉なことだし、君の人生にとって、貴重な経験になると思うよ。
様々な希望や思いで入学してきた新入生の代表として、学校関係者や保護者に対して挨拶するわけだから、明るく元気に挨拶してほしいな。
四字熟語で言うなら、頭脳明晰で明眸皓歯な君なら、きっと印象的で明朗快活な挨拶ができると思うよ。」
「入学者代表として、具体的にどんなことを話したらいいのか分かりません。」
「最近では、春の高校野球大会での、石巻工業の主将の挨拶は素晴らしかったね。
話すべきポイントを押さえ、かつ被災地からの出場ということで、特別な思いもその言葉に入れ、しっかりと暗記し堂々とした態度で述べた代表の宣誓に、私は感動したし、多くの人びとを勇気づけたと思う。
本当に、話した内容に心がこもっていたんだろうね。
君に、この学校の入学に特別な思いがあり、また文章表現に自信があるなら、型通りの挨拶から離れ、個性的な内容で語るのも良い。
もしそうでなければ、代表挨拶として入れるべき内容と、話したい内容を個条書きにして、そこにあなたらしさをどの程度入れるか熟慮するという方法がいいと思うよ。
例えば、簡単な自己紹介・学校の指導方針を踏まえた志望校理由（遠距離通学しても入学したかった理由）・これからの高校生活の抱負と決意の表明・その先の将来の希望・最後に学校関係者および保護者への謝辞などや、震災からの復興・今年の厳寒の冬を耐えて咲く満開の桜・学校以外の活動・個人的に特別に話したいことなどを箇条書きにして、全体のバランスを考え取捨選択する。
そして、内容と内容のつながりや言葉遣いなどは、原稿用紙に書いて声を出して読み、周りの人に聞いてもらい、推敲していけばいい。」
「本番は、緊張するかも知れない。」
「しっかりと声を出して、本番をイメージして繰り返し練習することだね。
大切な部分は暗記して、原稿に目を落とさずに、前をしっかりと見て話すことも心掛けるべきだね。
私は、３０歳代の頃から、社員や趣味とする美術団体の知り合いから頼まれて、結婚式の仲人を引き受けたことがある。
式に参加する人たちの多くは、私よりも年齢が上の人たちで、そのために仲人としてのスピーチは、私なりの個性を生かし、すべて暗記して話したね。
新郎～さんは、父～氏と母～さんの長男として、昭和～年～月～日、～県～市でお生まれになりました・・・から、学歴の小学校・中学校・高校・大学の学校名と入学年そして卒業年まで暗記して、若輩の仲人だけれども、しっかりとやっているなという印象を与えるスピーチを心掛けたね。
私の近くのテーブル席から、『原稿を全く見てないね、全部暗記しているね！』という、ひそひそ話が聞こえてきたとき、してやったりと思ったね。」
たいへんなことになってしまったと言っていた彼女でしたが、そんな話しをしている内に、実際は新入生代表に選ばれたことに、嬉しさを感じているようでした。
原稿ができ次第、またアドバイスするつもりですが、他人の言葉でなく、彼女らしい自分の言葉で、入学の嬉しさと高校生活の抱負を元気よく述べれば、代表挨拶は成功裏に終わることでしょう。
彼女の高校入学式は、４月１０日。
その日、一人の少女の新たな第一歩が始まる。
（咲き始めた、４月５日の大島桜）
ブログ人気投票にクリックいただけると幸いです！
４月４日で、今年の春期講習も終了しました。
前日の３日は、猛烈に発達した低気圧のために、台風並みの暴風雨で全国的に被害が出ました。
教室では、小学生は予定時間よりも早く３時で授業を切り上げ、早退させました。
中学部は、状況を見て各自の判断で参加することとしましたが、予想に反してほとんどの生徒が授業に出席。
終了時刻の午後９時には、雨も止み風も比較的収まった状態になっていました。
教室の春期講習期間中に、すぐ近くのグリーンベルトに咲いている桜の下で、一日だけお花見ランチを楽しむことを恒例としていました。
しかし、今年は桜の開花が遅く、桜の下のお花見ランチは中止。
けれども、教室のランチタイムは、生徒にとって楽しい一時で、笑いが絶えません。
１日３時間から６時間の講習で、既習項目の総復習を行い、充実した学習が出来ました。
春期講習が終われば、いよいよ学校でも新学年がスタートします。
今年は私の故郷・雪国新潟と同様に、だいぶ遅れて満開になった桜が、入学式を華やかに彩ることでしょう。
ブログ人気投票にクリックいただけると幸いです！
一般の大人でも、小学校・中学校の学習内容をある程度覚えていると、クイズのように面白く解くことができる算数や数学の問題があります。
数理処理で、頭を活性化するために、ペンシルパズル『数独』の愛好者も多いのですが、もう少し幅を広げて、算数・数学を楽しんでは如何でしょう。
そこで、日頃小学生から高校生まで教えていて、一般の方にも解けそうで、パズルのようにおもしろい問題をこのブログで取り上げ、皆さんの脳の活性化に一役買いたいと思います。
今日は、最近中２の生徒から出た質問の問題を取り上げます。
【問題】
下の図のように、長方形ABCDを、線分POとOQで二つに分けてあります。
この左右の図形の面積を変えないで、点Qを通る直線で、この長方形ABCDを二つに分けたいと思います。
点Qを通る直線を作図してください。
細かく長さが指定されていれば、左右の図形の面積を求めて、点Qを通る直線で分けて作られる左右の台形の上底を求め、辺ADのその分点と点Qを結ぶことにより、作図が可能です。
今回の問題は、長さなどの指定がありません・・・さあどうしましょう。
【問題のヒント】
こうした問題を解くことが好きな人は、ヒントを見ないでチャレンジしてみてください。
問題のヒントの多くは、その問題を解くきっかけとなるもので、その問題の出題意図に関係する場合が多いのが常です。
「うちの子は、ちょっとヒントを与えると、確実に解答することができるんです。」と言うご父母が多いのですが、それはある意味当然です。
今回の問題は、下の図で示した「三角形の等積変形」を使います。
等積変形とは、三角形ABCの底辺BCに平行で点Aを通る直線L上に、点Aをどのように移動させても、その面積の大きさは変わらないというものです。
三角形の面積を求める公式は、底辺×高さ÷２ですので、底辺BCの長さは変化無く、平行線の上のいかなる点に頂点Aを移動しようとも、高さも変わらないので、三角形の形は変形しても面積は等しくなります。
【解答】
まず、点Pと点Qを結びます。
次に、点Oを通り、線分PQに平行な直線を引き、その直線と辺ADとの交点を取り、その点と点Qを結んだ直線が、求める直線となります。
ところで、直線上にない点を通りその直線に平行な直線を引く作図は、何通りかの考え方があります。
一つの方法を示しておきましょう。
直線Ｌに点Ｐから垂線を、下の図のようにコンパスを使って作図します。 
次に、作図した垂線上の点Ｐを通りその線に垂直な線ｍを、同じようにコンパスを使って作図します。
すると、直線Ｌと直線ｍは、平行線となり、作図が完了します。
ブログ人気投票にクリックいただけると幸いです！
今日は、中３から質問が出た数学の問題について考えてみます。
この問題は、一般的には中学３年で学習する範囲を含む問題ですが、中学受験を目指す小学生でも解答は可能な問題です。
さあ、ご一緒に考えてみましょう。
【問題】
中心をＯとし、直径をＡＢとする半円がある。下の図のように、弧ＡＢ上に点Ｃ、点Ｄを、ＯＣ平行ＡＤとなるようにとる。ＡＢ＝９，ＢＣ＝３のとき、線分ＡＤの長さを求めよ。
この問題は、ヒントを与えられると比較的簡単に解くことができます。
この問題のように、条件が不足しているようなシンプルな問題ほど、生徒は解くきっかけがつかめずに、考えこんでしまうことが多いようです。
下の図を見ないで、まずは上の問題と図から考えてみてください。
【解き方】
まず与えられた問題条件を図に整理してみましょう。
内接する四角形・平行線と角・三平方の定理・三角形の相似・円周角と中心角などが関連する可能性があり、まずそれらを念頭に置いて考えていきます。
角Ａと角ＣＯＢは平行線の同位角だから、角Ａ＝角ＣＯＢ
三角形ＯＤＡは辺ＯＡと辺ＯＤは半径だから、二等辺三角形。
よって底角は等しいから、角Ａ＝角ＯＤＡ
また、角ＯＤＡと角ＤＯＣは平行線の錯角だから、角ＯＤＡ＝角ＤＯＣ
（このことより、上の図で示した●の角はすべて等しくなります。）
また、三角形ＯＢＣと三角形ＯＣＤはそれぞれ半径を２辺とする二等辺三角形で、かつ頂角が等しいので、合同な三角形です。
（×で示した底角の大きさは、等しくなっています。）
ここまで問題条件を整理しても、三平方の定理などは使えず、線分ＡＤの長さを求めることが出来ません。
そこで、下の図のように、線分ＡＤをＤの方に延長し、線分ＢＣも同様にＣの方に延長してその交点をＥとおきます。
（こうした考え方の流れは、生徒に順を追って説明した手順であり、私が解法するために考えた手順でもあります。）
すると、内接する四角形の性質より、内対角の和が１８０度になることから、角ＢＣＤの外角である角ＤＣＥと角Ａは等しくなります。
（角Ａ＋角ＢＣＤ＝１８０度、また角ＢＣＤ＋角ＤＣＥ＝１８０度、よって角Ａ＝角ＤＣＥ）
また、角ＣＤＥと角ＯＣＤは平行線の錯角なので等しくなります。
（相似条件で角ＤＣＥと角Ａが等しいを使わずに、角ＣＥＤと角ＯＣＢは、平行線の同位角で等しいいを使ってもよい。・・・こちらの方が小学生に対する説明としては良い。）
このことから、三角形ＯＢＣと三角形ＡＢＥと三角形ＣＥＤは相似な二等辺三角形であることが分かります。（相似条件：２角相等）
ＡＢ＝ＡＥ＝９であり、ＡＤ＝ＡＥ－ＤＥなので、相似の関係から、後はＤＥの長さを求めることができれば、ＡＤの長さを求めることができます。
三角形ＯＢＣにおいて与えられた条件から、ＯＢ：ＢＣ＝４．５：３＝３：２
三角形ＣＥＤにおいて、ＣＤ：ＤＥ＝３：X
よって、３：X＝３：２という比例式が成り立ち、ＤＥの長さであるX＝２を求めることができます。
求める線分ＡＤは、ＡＤ＝ＡＥ－ＤＥ＝９－２＝７
この問題は、三角形の相似を広く使うために、補助線を引いて考える問題でした。
小学生でも、与えられた条件を整理し、内接する四角形の性質を使わなくとも、三角形の相似を説明できるので、上手く補助線が引ければ、解答することが可能な問題です。
小学生に対しては、予め必要な補助線を引くか、質問が出た段階でヒントとして補助線を引いてあげると良いでしょう。
ブログ人気投票にクリックいただけると幸いです！
ジェネレーションの違いにより、使われる言葉の違いを感じることがあります。
小学生・中学生・高校生、そして幅の広い年代の大人と話し、時に生徒の文章を添削するようなとき、そうしたことを痛感することは、稀ではありません。
今日は過日、公立小学校５年生の学習で、宮沢賢治の「注文の多い料理店」を題材にして国語の授業をしたときの出来事について、ちょっと考えてみたいともいます。
「立派な青い瀬戸の塩つぼは置いてありましたが、～」という文面があり、その中に出てくる「瀬戸」について少し解説しましたが、そのときびっくりしたことを今日はお話しましょう。
（伊志良 光 染付葡萄四十雀文皿・・・磁器）
まず黒板に「瀬戸」と書いて、「この言葉は地名を表していますが、どの辺りにある地名でしょう。」と生徒に問いかけました。
すると案の定、瀬戸内海周辺の地名ではないかと言い出す生徒がほとんどで、正解者は無し。
そこで正解である愛知県の瀬戸の地域について話をしました。
瀬戸地方は、陶器の一大産地であり、その結果一般的な陶器・焼き物を指して、瀬戸物と呼ぶようになったという経緯を話しました。
ところが、驚くことにほとんどの生徒は、瀬戸物という意味が理解できませんでした。
（井上 万二 シノギ煎茶セット・・・磁器）
「君たちは、ご飯の茶碗を、一般的に何といいますか、」
「もちろん、お茶碗。」
「そうじゃなくて、一般的に皿のような焼き物を、何と呼びますか。」
「お皿」
・・・・・・？
（浦口 雅行 青磁香炉・・・陶器。多くの方が勘違いされているが、日本で人気と評価の高い青磁は土もの・陶器の青磁）
「君たちは、茶碗や皿のような焼き物を、『せともの』と言いませんか。」
「『せともの』？・・・知りません。」
もちろん知っていた生徒もいたのでしょうが、少なくとも過半数の生徒が、「せともの」という言葉を、聞きなれない言葉として認識したのに、私は驚かされました。
私の世代では、常識として認識している言葉が、今の子どもには違和感を持って捉えられてしまうことがあるようです。
言葉は常に大衆の中で意味も用法も時間と共に変遷し、新しい言葉が生まれ、また死語となってしまう言葉もあるという事例の一つとして、「せともの」という言葉を挙げることができるでしょう。
（北大路 魯山人 黄瀬戸茶碗・・・陶器）
日常使っている茶碗や皿といった焼き物は、陶器（透過性が無く厚手で重い土物の焼き物）や磁器（半透過性の硬質な焼き物）で出来ています。
それらの焼き物を総称して、東日本では瀬戸物、西日本では唐津物と呼び習わされてきました。
では、いったいいつ頃から、「せともの」という呼び方が、特に子どもたちの会話から消えてしまったのでしょう。
かつて小売店が軒を並べた商店街が興隆していた時代、その商店街には必ずといって良いほど「せともの屋」があったはずです。
焼き物を専門に扱う「せともの屋さん」は、子どもにとって馴染みのお店屋さんでした。
しかし、現在では、スーパーや百貨店の売り場の一部で、そうした焼き物を売っているので、焼き物を総称した「せともの」という言葉を使うことがなくなり、単に食器売り場と呼ぶようになりました。
そうした食器売り場で買い物をする時代では、「せともの」という言葉を使う必要がなくなってしまったと考えられます。
（竹中 造 白磁シノギ盃・・・磁器）
もう一点気になることがあります。
これは、一般的な大人でさえ理解していない人もいると考えられますが、私たちが日頃使っている焼き物には、大きく二種類の焼き物が存在します。
一つは、白い石粉（磁土）を練り上げ高温で焼成した焼き物で、叩くとガラスのような硬質な音がして、光にかざすと光を透過する物、すなわち最近の食卓にのるほとんどの食器が、このタイプの焼き物で、正式には磁器（石もの）と言います。
見た目にも清潔感があり、大量生産に向いた焼き物です。
二つ目は、粘り気を帯びた陶土を練り上げ、土の風合いを生かした焼き物で、叩くと鈍い音がして、光は透過せず、中には若干吸水性のある焼き物、これを陶器（土もの）と言います。
陶器と磁器を合わせて、焼き物全体を熟語で陶磁器と呼びます。
（加守田 章二 灰釉茶碗・・・陶器）
本来瀬戸は、陶器（土もの）の代表的な産地ですが、家庭で使う食器がほぼ大量生産された磁器であることから、それらの焼き物を「せともの」と呼ぶことが不自然になったことも、「せともの」という言葉が廃れた原因の一つかも知れません。
小中学生のお子さんがいらっしゃったら、また小中学生を指導していたら、念のため「せともの」について認識しているかどうか、確認してみてください。
ほとんどが、「知らない」と答えることでしょう。
もっと言うなら、このブログをご覧のあなた、あなたが若い方であれば、もしかしたら既にあなたの世代でも使われなくなった言葉の一つに、「せともの」が該当している可能性さえあるでしょう。
同じ言葉が、世代間で異なる意味で認識されたり、使われてきた言葉が死語になったり、新たな造語・新語が流行ったりと、めまぐるしい現代を映すかのように、言葉の変遷も激しいようです。
こうした例を、ブログの読者の方から、今度は私にお知らせいただければ、嬉しいのですが・・・。
（大樋 長左衛門 あめ釉茶碗・・・陶器）
（今井 政之 象嵌彩塩窯黄水仙花壷・・・陶器）
注：昨年末、大樋長左衛門は文化勲章を、今井政之は文化功労者に推挙されました。
ブログ人気投票にクリックいただけると幸いです！
今日の午前中は、私が受け持つ区立中学校３年数学の、今年に入って初回の授業がありました。
中３受験生にとっては、私立推薦入試、都立推薦入試、私立一般入試、都立一般入試の順で、入試が行われる受験シーズンに突入しました。
（１月１０日、公園の青い空に赤いサザンカ）
今日の学習テーマは、数学応用コースの入試対策「円周角」で、中２の最後で学習した内容ですが、比較的習熟度が低い項目と言えます。
「円周角と中心角の関係」「二等辺三角形の性質」「平行線と角」「三角形の外角の定理」「三角形の合同および相似」「接線の性質」など、既習項目を使って、解いていく問題です。
こうした図形の問題を解かせると、基本的な項目を知ってはいるけれども、それを上手く使いこなせない生徒が多くいます。
今回学習したような図形の問題は、「図形的なセンス」が有るか無いかで、解けるか解けないかが決まるとも言われています。
しかし、その図形的センスとは、基本をしっかりと覚えた後に、それを使いこなせるように練習したかどうか、その結果として知識が経験として身に付いているかどうかということです。
隠れた条件や解く道筋を、与えられた問題から見つけるということは、そうした過去の経験に照らし合わせて導き出すということに他ならないからです。
何か新しい考えを発想するということも、実はその多くが過去の経験や知識から類推し発展させたものと言っても過言ではありません。
（１月１０日 公園のパンジー）
ところで、この時期になると、緊張が高まってくる公立中学校の受験生の中に、やけに気の抜けた生徒がいることに気づきます。
それらの生徒は、私立の推薦入試（単願）により、ほぼ確実に合格する学校が決まった生徒たちです。
そうした生徒に対しては、「高校数学は、そんな甘いもんじゃあないよ。中学で習った基礎事項をしっかりとマスターして、高校へ進学しなさい。」と、私は声掛けします。
「でも先生、俺の行く学校は、たいした学校ではないから。」
「自分のこれから入学しようとする学校を、そんなふうに考えてはだめだよ。」
「だって先生、俺さえも入学できる学校だよ。」
「さえ？さえなんて言っちゃあだめだな。もう少し自分にプライドを持たなければ。」
今日、そんな会話を、単願で行く学校が決まった生徒としました。
そうは言ったものの、自分にプライドを持つことは、実はそんなに容易ではないことかもしれません。
仮に簡単にプライドを持てたとすれば、それはプライドではなく、はったりと呼んでも差し支えないものでしょう。
たぶん、今日の生徒がプライドと呼べるものを持てたと感じることがあるとすれば、例えば「今日の５０分の授業をまじめに集中して出来たぜ！」といったレベルの小さな成功体験の積み重ねと少なからぬ努力の上に、成立することだろうと思います。
いつか、その生徒の「俺でさえ」という枕詞が、
「俺にはできる！」というポジティブな言葉に、
変わっていくことを、私は願っています。
（１月８日 公園の綿毛に包まれたコブシの冬芽
冷たい北風に揺れながら萌え出づる春を待つ）
ブログ人気投票にクリックいただけると幸いです！
今日私が取り上げる写真は、高校１年英語教科書に載っていたものである。
そこで生徒に教えた内容はちょっと脇に置いて、私がこの写真を見て考えさせられたことを取り上げたいと思う。
これはかつてテレビにも取り上げられたほど有名な写真なので、すでに多くの方がご覧になっているものと思われる。
この写真は、米軍の従軍カメラマンのジョー・オダネル（Joe O'Donnell）が、原爆投下直後の長崎に入り撮ったものである。
題材は、亡き弟を背負った被災少年が、弟を荼毘に付すために順番を待っている姿を撮ったもので、題名は「焼き場に立つ少年」という写真である。
The boy stood there straight without moving ,watching the flames. He was biting his lower lip so hard that it shone with blood. The flame burned low like the sun going down. The boy turned around and walked silently away.
１０歳ほどの少年の身に突然訪れた惨劇。
彼の両親や祖父母など、身内はどうしたのだろう。
無縁仏となった人たちを、共同で火葬する場所を設けたことを、この少年は周囲の人の助言を得て知り、死臭が漂い始めた幼い弟の亡骸を負ぶってやってきたのだろう。
彼が背負ったのは、単に幼い弟の亡骸だけではない。
あまりに悲惨で苦渋に満ちた受け入れ難い運命を、この少年はどう受け止めたのだろう。
ほんの小さな世界しか経験したことの無い少年が、押しつぶされそうな現実に直面する運命を背負う世界など、神も仏もあったものではない。
実はこの写真から受けた思いは、カメラマンが意図した原爆の悲惨さや反核の大儀などは隅に押しやられ、一人の少年に訪れたどうしようもない運命を、この後どう受け止め乗り越えていくのかという重い命題だけが、私の脳裏を回転し始める。
従軍カメラマンとして、原爆の破壊力を記録する一方、軍に隠れ原爆の惨状を記録したジョー・オダネルは、４３年間そのネガを封印後、原爆の悲劇を訴えるためにそれらの写真を公開する。
その彼の行為に対して、偏狭なアメリカ社会から厳しい非難をうけただけではなく、家族の離散をも経験する。
そうした苦難の道を歩んでも、原爆の悲劇を訴え、非核の運動を展開したジョー・オダネルがいて、初めてこの写真を私たちは目にすることができる。
この写真は、自分の命運を賭する覚悟でこの写真を公開した、一人の勇気ある写真家の生き方も、投影されている。
土門拳が語った「絶対非演出の絶対スナップを基本方法とするリアリズム写真」という言葉は、リアリズム写真のスローガンと言っても良い。
しかし、写真家がファインダーを覗き、そこに映った映像を彼自身の網膜に投影した時から、「絶対非演出」など有り得ないと、私は考える。
仮にそれが報道写真だとしても、カメラマンがその対象にレンズを向けた途端に、事実の一端を記録したつもりで、実のところは写真家の「演出」が入り込んでいると私は思うからだ。
無論、今日紹介した写真もその例外ではなく、事実を記録しているとともに、この写真家が思ったことが雄弁に記録されていると言ってよい。
したがって、彼がこの写真の対象である情景に出会って、その事実を記録しようとシャッターを切ったその瞬間から、この写真を公開することに対しどんなに抵抗があろうと、写真を世に出して原爆の悲惨さを訴えかける使命を、彼は背負ってしまった。
それほどに、この写真が記録した情景に、人を突き動かす力がある。
ジョー・オダネルが好むと好まざるとに関わらず、
この世に起きた痛ましい現実を世に問う使命を、
彼は十字架の如く背負ってしまったと言ってよい。
ブログ人気投票にクリックいただけると幸いです！
とても条件がシンプルな問題の為に、逆に生徒たちが解く手掛かりを見つけられずに、迷ってしまう問題があります。
今回の算数の問題は、先日小学６年生が解けずに質問に来たもので、このブログでもしばらく前に取り上げた、ある重要な基本事項に気づくかどうかが、成否の分かれ目となります。
問題の条件は、以下のようなものです。
まずは、答えを見る前に、ご覧の皆さん、チャレンジしてみてください！
この問題を解く条件は、公立小学６年生までに習ったものです。
【問題】
点Ｏを中心とする半径１０ｃｍの半円の円周上の点は、半円を６等分する点です。斜線の部分の面積を求めなさい。円周率は３．１４とし、答えは小数第２位を四捨五入して小数第１位まで答えなさい。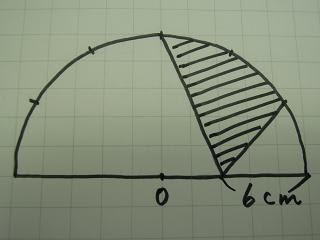
ところで本題に入る前に、以上の条件で分度器を使わずコンパスと定規だけで、この問題を作図できますか。
その方法も大切なので、説明しておきましょう。
コンパスで半円を描き、そのコンパスの足の開きを変えずに、弧をコンパスで分けていくとちょうど３等分されます。
すると正三角形が３つ内接した図を描くことができます。
この描き方は、中学入試の正多角形の中で、出題率の高い正六角形を描く方法と同じです。
円を描いたら、コンパスの開きを変えずに、円周を分割するとちょうど６等分でき、その点を結ぶと正六角形を描くことができます。（コンパスがあったら、お子さんとやってみてください）
次に中心角６０度の二等分線を描く要領で線を引き、円周と交わった点を決めると、半円の円周（弧）を６等分することができます。
さて、ご覧の皆さん、この問題を解けたでしょうか。
【解き方】
小学６年生が質問したこの問題を、中学３年生に出題すると、「円と角」「三平方」「等積変形」など、いろいろ浮かんできたキーワードを使うかどうか、私に確認してきます。
条件があまりに少ないので、どういった手法で解くのか、生徒は迷うからです。
最も勘違いしやすいのは、右下の図形を、半径６ｃｍのおうぎ形と見てしまうことでしょうか。・・・もちろんそれは間違いで、おまけにそうだとしてもその中心角はどうやって求めるの？
こうした求積問題の解き方は、求める図形を「分けて考える」か、または求める図形を含む図形から「余分を引く」かの二通りがあります。
この問題は、求める図形を含む四分円から余分を引くことにより求めます。
四分円(中心角９０度、４分の１円）の面積から、辺の長さが１０ｃｍ・４ｃｍの左の直角三角形と、右下の一見おうぎ形のような図形の面積を引けば、斜線部分の面積を求めることができます。
この考え方までは、多くの生徒が到達します。
ただ、右下のおうぎ形のような図形の面積を、どう求めたらよいか考えるうちに、この方法が間違っているのではないかと、あらぬ方向へ思考がずれてしまいます。
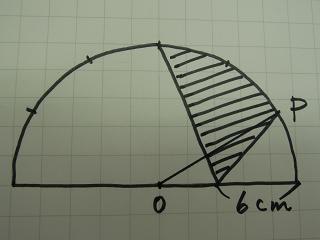
実は、最初に思いついた四分円から余分を引くという考え方で正解です。
では、右下のおうぎ形のような図形の面積の求め方を、教えましょう。
まず、上の図のように中心Oから円周上の点Pに半径を引きます。
今度は下の図をご覧ください。
右下の図形PQRの面積は、おうぎ形PORから三角形POQを引くことにより求めることができることが分かります。
さて、問題は三角形POQの底辺４ｃｍは出ていますが、頂点Pから底辺に下ろした高さが出ていません。
しかし、三角形POQの高さを一辺とし、斜辺を半径１０ｃｍとする直角三角形の角度は３０度・６０度・９０度となっていることに注目します。
三角定規の一つでもあるこの直角三角形の斜辺と、今回高さとした辺の長さの比は、２：１であることは、小４レベルの学習ですでに理解していなければなりません。
本格的な直角三角形の辺の比については、中学３年生の三平方の定理で学習しますが、今回の直角三角形の辺の比が、２：１であることは基本です。
このことから、高さは斜辺の半分の５ｃｍであることが分かりますから、三角形POQの面積は、４×５÷２＝１０（平方センチメートル）となります。
この三角形の面積を、中心角３０度のおうぎ形から引くことにより、右下の図形PQRの面積を求めることができます。
よって求める斜線部分の面積は、
（四分円の面積）－（底辺４ｃｍ・高さ１０ｃｍの直角三角形）－｛（おうぎ形ＰＯＲ）－（三角形ＰＯＱ）｝
１０×１０×３．１４×１/４－４×１０÷２－（１０×１０×３．１４×１/１２－４×５÷２）
＝１０×１０×３．１４×（１/４－１/１２）－２０＋１０
＝３１４×１/６－１０
＝５２．３－１０
＝４２．３（平方センチメートル）
中学生以上は、円周率πを用いて計算してかまいません。
１０×１０×π×１/４－４×１０÷２－（１０×１０×π×１/１２－４×５÷２）
＝１００π×（１/４－１/１２）－１０
＝（１００／６）π－１０
＝（５０/３）π－１０・・・分数表記ができないので（ ）を使用。
基本的な事柄を覚えていても、
それを使いこなせるようにしておかなければ、
真に覚えているとは言えません。
ブログ人気投票にクリックいただけると幸いです！
中２の生徒から、下図のような問題の解き方についての質問がありました。
中学数学の学習領域を知っている方は、この問題が「三平方の定理」を使う問題で、公立中学校では、およそ中学３年の後期で取り扱うことが分かるでしょう。
この生徒は、私立中学校に通っている中２ですから、公立よりも先取りの学習内容です。
「三平方の定理 基本練習」と書かれたプリントに載っていた問題ですが、簡単なようでちょっとした工夫が必要な興味深い問題ですので、今回のブログに取り上げたいと思います。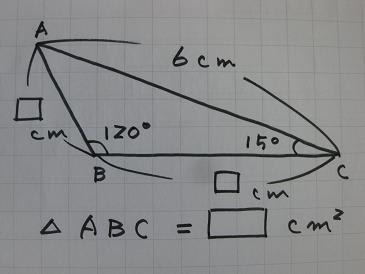
上図のようにとてもシンプルな条件が示され、辺ABと辺BCの長さ、⊿ABCの面積を求めよ、という問題です。
さて皆さんなら、この問題をどう生徒に解説しますか・・・無論待った無しで！
「基本練習」というよりも、先取り学習の中２にとっては、「応用練習」と銘打った方が良かったかも知れません。
後日、この問題を教室の公立中高一貫校に通う中３生に出題してみました。
（中高一貫校の生徒は、すでに高校数Ⅰ・数Aの範囲を学習していますが、公立の中３生は、三平方はまだ未学習分野）
すると、彼は角度が１５度という数値から、辺ＢＣを対称の軸とする、線対称な図形を下に書き始めました。
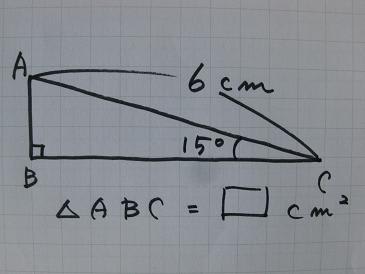
彼は、上図のような直角三角形の面積を求める方法から類推して、この問題を解こうとしたのです。 この考え方は、中学受験生にとって基本的な考え方が含まれますので、最初の問題から少し離れて、彼が類推した考え方についてまず説明したいと思います。 この「直角三角形ABCの斜辺が６ｃｍ、鋭角が１５度であるとき、この三角形の面積を求めよ」という問題です。 この問題を解くには、下の図のように、辺BCを線対称の軸として合同な三角形をもう一つ付け、頂角３０度の二等辺三角形を書きます。 この二等辺三角形の面積を求めることは、実は基本的な問題です。
下の二等辺三角形ABCにおいて、頂角が３０度の場合、小学４年生で学習する基本事項を使い、簡単に面積を求めることができます。
この問題と同じように、半径６ｃｍの円に内接する正十二角形の面積も、同様な方法で求めることができます。
なぜなら、円に内接する正十二角形（正多角形はすべて円に内接する）は、下の二等辺三角形が１２個組み合わされてできている図形だからです。
上の図のように、頂点Bから対辺ACに垂線を引きその交点をDとすると、頂点Bから辺ACまでの距離BDが３ｃｍであることが分かります。
なぜなら、頂点Aを含む三角形は、角の大きさが３０度・６０度・９０度の直角三角形になっているので、辺BDの長さは辺ABの長さの半分、すなわち３ｃｍとななるからです。
正三角形を一本の対称軸で二つの合同な直角三角形に分けると、角の大きさが３０度・６０度・９０度の直角三角形が２個できますので、６０度の角をはさむ辺の長さは、２：１になることは容易に子どもに説明できます。
したがって、角が１５度・７５度・９０度の直角三角形の面積は、頂角が３０度の二等辺三角形の半分として求めることができますので、
６×３÷２÷２＝４．５平方センチメートルとなります。
この考え方を利用する問題は、中学入試によく出る基本的な問題です。
しかし、初めの問題に戻りますが、公立中高一貫生が思いついた上の手法では、今回の問題は上手く解くことができません。
数学が得意だと豪語している私立中３の生徒に、この問題を同様に出すと、相似及び三平方を使って（当然次の一手はこの方法ですが）解こうとするのですが、正解には至りませんでした。
「もうだいぶ昔にかなりやったんだけれども、忘れた！」と負け惜しみを言って、ギブアップ。
では、質問した中２の生徒に私が説明した方法を、最後に解説しましょう。
まず、辺ABをBの方向に延長し、頂点Cからその半直線に垂線を引きその交点をDとします。
すると三角形ADCは直角二等辺三角形になり、三角形BDCは見覚えのある角の大きさが３０度・６０度・９０度の直角三角形になっていることが分かるでしょう。
まさに三角定規２枚の特殊な三角形です。
この二つの三角形は、その辺の比を覚えておいて計算します。
まず、辺DC＝６÷√２（ルート２）＝３√２（３ルート２）
次に辺BD＝３√２÷√３＝√６（ルート６）
よって求める辺BC=√６×２＝２√６・・・答え
辺AB＝辺AD－辺BD=３√２－√６・・・答え
最後に、三角形ABCの面積は、三角形ADCの面積を、AB:BDの辺の長さの比で比例配分することにより求めます。
⊿ADC＝３√２×３√２÷２＝９
⊿ABC＝９×{（３√２－√６）÷３√２}＝９－√３・・・答え
{ }の中が、比例配分の式
今回質問された問題は、基本事項を使えば答えを出すことができますが、補助線を引くことにより解く道筋が見えてくる問題でした。
日ごろ学習した経験を、自分の知識にまで昇華し、
その知識を、実際に活用できるレベルに習熟することが必要です。
ブログ人気投票にクリックいただけると幸いです！
３月２８日に、東京のソメイヨシノの開花が発表されました。
春爛漫の季節が、着実に時の歯車を回すように近づいています。
ただ今年に限っては春到来の嬉しさよりも、大震災で被災した多くの人たちの困難な生活や、行方不明者も含めた多数の尊い命が奪われた出来事が、重低音となって私たちの精神を震わせています。
また、福島原発事故によって発生した放射性物質は、被災地を越えて広範囲な人々に、目に見えない津波となって、襲いかかっているようです。
私が物心ついて以来、こんなに大きな影響を与えた社会的出来事があっただろうかとふと考えてしまいます。
６０年安保・東京オリンピック・大阪万博・オイルショック・バブル崩壊・阪神淡路大震災……。
私がかつて経験した出来事の中で、今回の震災ほど大きなインパクトを社会に与え、またこれからも与え続ける出来事は無かったように思います。
今回の震災によって、一人ひとりが様々な思いで世の中の事を考え、自分の人生を見つめ直し、家族の事を熟慮したに違いありません。
大震災の惨状が脳裏に焼きつき、例年とは異なる私たちの心情をよそに、周囲を見渡せば、さまざまな春の草木の花々が咲き始めています。
苦悩と混乱と不安の中で右往左往する私たちに降り注ぐ日差しは、明らかにその強さを増し、震災地の時計が２時４６分で止まっても、自然の営みの時計は確実に回り続けています。
「春の来ない冬はない！」…春遅い東北の地にも、被災者の心と体を温める春の日差しが降り注ぎますように！
寒咲大島
河津桜やカンヒザクラそして寒咲大島などの早咲きの桜は葉桜となり、コブシやモクレンの白い花が、ソメイヨシノの花の盛り前に存在感を示します。
公園にある東屋前のユキヤナギの花が、風に揺れて咲いていました。
ユキヤナギ
ユキヤナギ（雪柳）は、バラ科の落葉低木。別名にコゴメバナ、コゴメヤナギなど。
春に小さい白い花を咲かせる。中国原産という説もあるが、日本原産であると考えられている。
２６日から始まった春期講習は、中盤をむかえ受験学年を中心に、熱気ある授業が展開されています。
余震や放射性物質に敏感になっていた生徒も、ようやく落ち着きを取り戻しつつある状況です。
ただ、いつなんどき状況の変化があるかもしれませんので、常に情報を入手しながら授業を進めています。
例年、春期講習の一日の昼食時間に、すぐ近くの桜の下でお花見ランチを実施しています。
しかし、今年はそんな気分にはなれず、どうしようかと迷っています。
ところで、講習会の前に今年大学に合格した元会員が訪ねてきてくれました。
共立女子大附属と東京女学館の生徒たちですが、目指す大学に合格して嬉しそうでした。
今年は他に、攻玉社・三輪田・お茶の水女子大附属の生徒も、結果を報告に来てくれました。
桜咲く今年の春に、それぞれが新たな道を歩み出したようです。
お花見ランチをする桜の下では、例年夜桜見物の場所取りのシートが敷かれて、夜にはほろ酔い気分の花見客の楽しそうな声が聞こえましたが、今年はそういった気分になれない人が多いと思います。
かつてあった教室の軽井沢セミナーハウス周りには、春になるとコブシの花が一斉に咲きました。
５月の連休頃が見頃で、コブシの花が咲くこの時期に、やっと遅い春が軽井沢に訪れると言った印象がありました。
山で見かけるコブシは、公園で見かけるコブシよりも花の大きさは小さい分、花の数は多かったように思います。
コブシよりも一回り大きな白い花を咲かせているのは、ハクモクレンの木です。
ハクモクレンは、ハナモクレンとも呼ばれているようです。
３月末の公園に、真っ青な空に向かって、白い清楚なハクモクレンの花が一斉に咲いていました。
ハクモクレン（白木蓮）はモクレンの仲間で白色の花をつける。
しばしば、「モクレン」と混同され、そう呼ばれることがある。
モクレン属の中では大型の種類で樹高は10-15m程度まで成長する。
春、葉に先立って大形で白色の花が開く。
コブシの花
コブシ（辛夷）はモクレン科モクレン属の落葉広葉樹の高木。早春に他の木々に先駆けて白い花を梢いっぱいに咲かせる。別名「田打ち桜」。
ブログ人気投票にクリックいただけると幸いです！
冬型の気圧配置が安定しているせいか、東京は快晴が続いています。
冬期講習と正月特訓が連続して行われた冬の講習が、今日で終了しました。
ちなみに小学生については、小４が３時間の授業に３時間の補習。
小５が６時間の授業に１．５時間の補習。
小６が６時間の授業に４．５時間の補習。
小４は、午後の授業の他に、お弁当持参で午前中から自主的に３時間の補習を希望し、実行しました。
受験生だけではなく他の学年の生徒たちも、与えられた課題を消化して、充実した冬休みを過ごすことができたと考えています。
ところで毎年１月７日の朝食、我が家では決まって七草粥をいただきます。
スーパーなどでセットされている春の七草《セリ、ナズナ、ゴギョウ、ハコベラ、ホトケノザ、スズナ(カブ)、スズシロ(ダイコン)》を購入して作ることもあります。
また入手できた一部だけを入れたり、代用品となる青菜を入れて頂くこともあります。
『七草粥』と言っても、厳密に考える必要はないと思います。
お節料理やお餅で少し食傷気味な時期に、胃には優しく、そして新春を視覚と嗅覚そして味覚で味わうことのできるお粥をいただくという本来の趣旨に則っていればよいと思います。
講習に参加している小学生に、今朝七草粥を食べたかどうかを質問すると、僅かに一人だけ手を挙げました。
このことから、七草粥を年中行事として、１月７日に朝食で食べる家庭の割合は、現在の消費税の割合５％よりも少ないのではないかと推察されます。
かつての習慣や風習は、核家族化などの影響で、次の世代にバトンタッチされない状況があるようです。
そのことは、必ずしも悪いことだけではないのですが、先人の知恵が詰まった日本の伝統が失われていく側面を考えると、寂しさも感じます。
春の七草と秋の七草の覚え方など興味ある方は、以下のブログを参考にご覧ください。
マッキーの教室：秋の七草・春の七草…その覚え方
クリスマス飾りと異なり、正月飾りは短期間で仕舞い込むことになります。
正月飾りを片付け、成人式が過ぎれば、受験シーズンに突入します。
受験生のいる家庭では、最善の状態で受験し、存分に実力が発揮できるように配慮しなければなりません。
かつてのブログで、「入試直前の過ごし方」と「受験日前日と当日の注意点」についてアドバイスしました。
「塾教師」として、そして「受験生の親」としての経験を基に、かなりレベル高くまとめたものです。（自画自賛）
受験生をお持ちの家庭は、ぜひ参考にして下さい。
マッキーの受験必勝アドバイス…（１）入試直前の過ごし方
マッキーの受験必勝アドバイス（２）受験日前日と当日の注意点
体調を整えて、最善を尽くして、志望校合格を目指そう！
悪魔のように細心に、天使のように大胆に、怠り無く準備しよう！
「 Do your best, and let it be．」
勝利の女神は、必ず君たちに微笑むと、私は信じている
２０１０年、今年もどうぞよろしくお願い致します。
私は、年末年始も無く受験生を中心に学習指導に昼夜頑張っています。
年が明けると、いよいよ受験シーズンに突入する緊張感を感じます。
今年の初日の出
元旦は、ベランダから初日の出を拝みました
唯一の休みの元旦に風邪をひき、少し体調不良でしたが、熱気溢れる受験生を中心とする講習指導で、風邪も吹っ飛びました。
年末そして年始、怒濤のような講習の合間に、ふと感じる時の流れ。
玄関の正月飾り
お節料理
新年２日早朝の、静かな明治座前の通り
１月４日（月）…まだ休みも多いようで、静かな町中でした。
冬期講習６日目
１月５日（火）…近くのビル工事現場も、槌音が響き始め、日常の雑踏が戻ってきました。
君ら…何してんの？…昼の休憩時間
１月７日（木）…朝、七草粥をいただきました。
湯気が立つ七草粥…講習会最終日
今日で、冬期講習が終了し、明日からは平常の授業に戻ります。
来週からは、私の公立小中学校の指導も再開します。
そしていよいよ中学受験では、埼玉・千葉方面の学校の入試がスタートし、
また高校受験では、私立そして都立の推薦入試が始まります。
人気投票に、応援のクリックをお願いします
人気投票に、応援のクリックをお願いします
私は、年末年始も無く受験生を中心に学習指導に昼夜頑張っています。
年が明けると、いよいよ受験シーズンに突入する緊張感を感じます。
今年の初日の出
元旦は、ベランダから初日の出を拝みました
唯一の休みの元旦に風邪をひき、少し体調不良でしたが、熱気溢れる受験生を中心とする講習指導で、風邪も吹っ飛びました。
年末そして年始、怒濤のような講習の合間に、ふと感じる時の流れ。
玄関の正月飾り
お節料理
新年２日早朝の、静かな明治座前の通り
１月４日（月）…まだ休みも多いようで、静かな町中でした。
冬期講習６日目
１月５日（火）…近くのビル工事現場も、槌音が響き始め、日常の雑踏が戻ってきました。
君ら…何してんの？…昼の休憩時間
１月７日（木）…朝、七草粥をいただきました。
湯気が立つ七草粥…講習会最終日
今日で、冬期講習が終了し、明日からは平常の授業に戻ります。
来週からは、私の公立小中学校の指導も再開します。
そしていよいよ中学受験では、埼玉・千葉方面の学校の入試がスタートし、
また高校受験では、私立そして都立の推薦入試が始まります。
人気投票に、応援のクリックをお願いします
人気投票に、応援のクリックをお願いします