『算数の教え方教えますMother's math』in東京☛ホームページはこちら
『海外在住のお子様の学習サポート』
☞『海外在住の日本のお子さまのオンライン学習サポートのホームページ』
『長期入院、長期療養のお子様の学習サポート』
☞『長期入院・長期療養のお子様のオンライン学習サポートのホームページ』
4月初っ端なのに、6年生だけはすでに濃い内容を習っていると思います。今やっている単元(内容)は『対称な図形』でしょうか?(進度は各教科書会社によって異なるので、「対称な図形」からやっていない学校もあります。)
この『対称な図形』特に線対称と点対称ですが、これは何かと教えずらい単元であるかと思います。そこで、ちょとしたコツをお伝えしてみようと思います。
この線対称と点対称自体をお子さんに教えるにも、「線対称=ある直線を折り目にして、重なる図形」「点対称=ある1点のまわりに180°回転した図形」という説明だけでは、分かったような分からないような 感じでの理解になり。このあやふやな理解のまま、問題を解こうとすると、何をどう考えれば?
感じでの理解になり。このあやふやな理解のまま、問題を解こうとすると、何をどう考えれば?
また、折り目にして重なる図形(線対称)・・・ということは、問題解くときにその問題用紙を折りたくもなってきます 。
。
実際に紙を折ったり、1点を中心に180°図形に回すことは学校の授業でしっかりやるところだと思いますので、そちらにお任せしましょう 。
。
今回お伝えするコツは、線対称と点対称について、いきなり図形での対称ではなく、点での対称を先に考えます。
[1] 点の対称移動
実際に、次の点Aのそれぞれの対称の点をお子さんに記させてみてください。
お子さんは上手く点Bと点Cを打てましたか?
そして、点Bと点Cを記すことが出来たお子さんも、それが線対称、点対称であるという記号は書けていますか? 線対称、点対称であるという記号❓❓❓
このブログをずっと読んで下さっている方は何度もお伝えしました『図形問題の攻め方』(2月14日ブログ参照)図形問題を強くさせる(図形を素早く処理する、見間違いを防ぐ)ためには記号を入れてくださいと強く言ってきました。例えば、長さが等しいの記号||だったり、直角の記号だったり、
ここでも、線対称、点対称を記号で合わすことが図形の捉え方をより強くさせます。
さあ、お子さんに記号も書いてごらんと促しながら、理解を深めてみましょう。
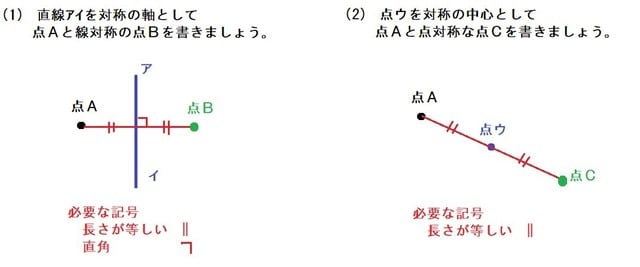
そして、記号が書けたならば、その図をみると次のようにも言えてきますね。
「直線アイを軸とする線対称は、2点A、Bのまん中の点を通り垂直である」
「点ウを中心とする点対称は、2点A、Cのまん中の点である」
(実は、この言い換えは高校2年の数Ⅱの「図形と方程式」を解くときに役立つ考え方なのですが、小学生においても記号を書いて図を見直すと十分理解可能なことですので、この機会にそっと身に付けてあげておくといいですよ )
)
では、小学生の実際の問題を使いながら、小学生の問題を考えてみます
[2] 図形の対称移動
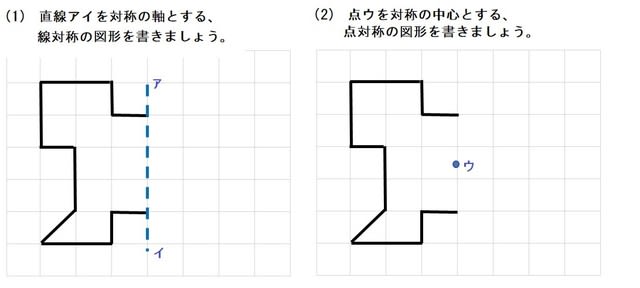
このような問題に対して、次のように考えて進めていくといいと思います。
まず『図形というものは点の集まりです。』
例えば、「線はたくさんの点が集まってできている」。同様に、「円や放物線も図形は点がたくさん集まって出来ています」。
これを逆に言うと
「線の上にはたくさんの点があります。」「図形の上にはたくさんの点があります」
だから、先に特徴のある点を動かしていきましょう。
もちろんこの時も、記号をいれるといいですね。
❶ 点を先に対称移動させる。
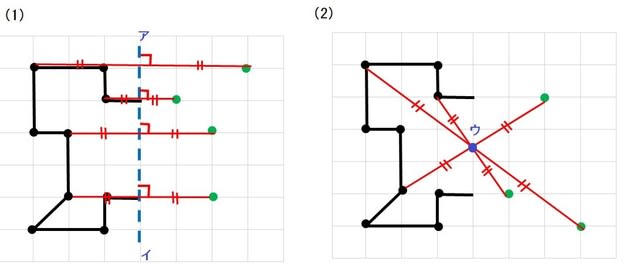
このように、先に図形の頂点を対称に書きます。
後は、もとの図形が「頂点と頂点を直線で結んだものなので」、対称に書いた点と点を直線で結べば出来上がりです。
❷ 対称に書いた点と点を結ぶ。
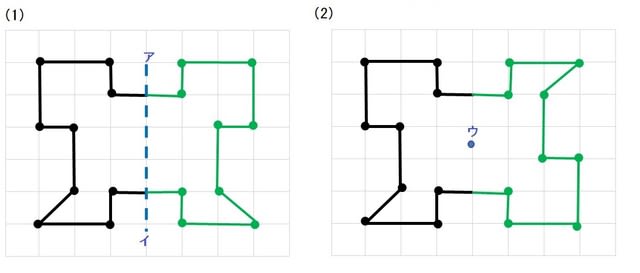
何となくの線対称や点対称の理解(線で折るとかのイメージだけの理解)で図形をじっとみながら、答えるのではなく。
具体的な点を正確に対称移動させた後に、図形を形どることをお勧めします。
今日のまとめ
[1]線対称と点対称を記号で表す。
[2]図形の対称をつくるには
❶ 点を先に対称移動させる。(対称を記号であらわす)
❷ 対称に書いた点と点を結ぶ。
そして「図形は点の集まりである」
また、図形は慣れも非常に大事なので、平日にもドリル等で易しめの対称問題をやるといいですよ。すぐ慣れます。
そして、今回のこの「図形は点の集まりである」という考えも高校2年生の軌跡という分野で扱うものでもあるのですが、このフレーズ「図形は点の集まり」をお子さんの頭の隅にでも残してあげておくと、高校のときにふっとよみがえってきます。(高校2年生でも軌跡がなにであるのか、分かってない子は多いです、図形は点の集まりという話を数式でいっているだけなのですが、またこの大事なフレーズは高校の教科書の軌跡のはじめの一文に書いてあることが多いのですが、教科書で勉強できない子が多くて、つまり始めから参考書でやろうとする子が多いので、大事な部分を見逃しているのです、、、、残念な勉強の仕方が身に付いてしまっているのです。教科書がベースです本当に力が付けたいなら・・・)
今日はかなり濃い内容でしたね!!
6年生は学年始めの4月から本腰入れて勉強した方がよろしいかと思います。










線対称な図形、点対称な
図形というのが得意です。しかし確認や予習のために
小林美代子さんのサイトをみさせいただきました。
ためになりました。
ありがとうございました。