「数学のゼロ」と「物理学のゼロ」では解釈が異なる？

　以前の基礎物理学の理論では、基本構成部品である粒子を、無限に小さいゼロ次元の点と見なしていた。
しかし、ひもは無限小の粒子ではないので、超ミクロスケールにおいて古典幾何学を悩ませていた量子ゆらぎは比較的大きな領域に広がり、強度が小さくなって取り扱えるようになる。
そうして、物理学を苦しめている、時空の曲率と密度が無限大に発散する特異点の問題をうまく回避できる。
アンドリュー・ストロミンガーは次のように言う。
「幾何学が破綻するような状況を研究したいなら、少しだけ破綻するケースを取り上げればいいだろう。そのためのもっともよい方法の一つが、カラビ＝ヤウ空間がどのように破綻するかを研究することだ。カラビ＝ヤウ空間では、時空が破綻する領域を分離し、残りの領域はよい状態に保っておくことができるからだ」。

　カラビ＝ヤウ空間というコントロールされた舞台でひも理論を調べていけば、量子幾何学とそれがもたらす事柄に関する何らかの洞察が得られるだろうという。
ひも理論の中で、幾何が古典幾何学においてとは異なる振る舞いをするような状況を探すという方法がある。
その例としてもっとも重要なのが、ひも理論では滑らかに進行することが多いが、従来の物理学ではそうでないトポロジーの変化を伴う転移だ。
「標準的な幾何学の手法に限定すれば、つまりリーマン計量を常に保てばトポロジーは変化しようがない」とモリソンは言う。
トポロジーの変化が一大事だと見なされるのは、何らかの方法で引き裂かないとある空間から別の空間へ変形できないからだ。
殻を割らないと卵をかき混ぜられない、あるいは穴をつくらないと球面をドーナツに変えられないのと同じだ。

　しかし、滑らかな空間に穴を開けると特異点ができる。
それによって一般相対論学者は問題に直面し、無限大の曲率係数のようなものと戦わなければならなくなる。
しかしひも理論は、その問題を避けられるかもしれない。
たとえば、１９８７年にガン・ティアンとヤウは、フロップ転移と呼ばれる手法を示し、密接に関連しているがトポロジー的に異なるカラビ＝ヤウ多様体の例を多数つくった。

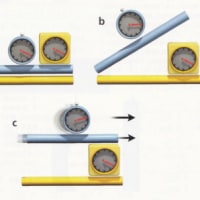
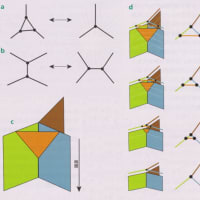
図２　「フロップ転移」について考える1つの方法として，まず，2次元の骨組みに縦のスリットを入れる。次にその骨組みを上下から押し，縦のスリットをどんどん広げて最終的に横向きのスリットにする。こうして，縦だったスリット，つまり裂け目が，横向きに「反転」する。カラビ＝ヤウ多様体でもフロップ転移をおこなうことができ，内部構造が（最初に裂いた後に）同様の方法でひっくり返り，最初のものとはトポロジー的に異なる多様体ができる。このフロップ転移が特別興味深いのは，それらの多様体はトポロジー的に異なるのに，まったく同じ4次元物理を伴うためだ。


コニフォールド転移は、カラビ＝ヤウ空間が関係するトポロジー的変化としてさらに劇的なもう一つの例だ。
図２に示したように、カラビ＝ヤウ空間の中で尖った先を下にして立つ、フットボールのような二次元曲面を考える。
このフットボールを潰してどんどん細いひもにすると、時空の骨組みに開いた裂け目　－　縦のスリット　－　だけを残すことができる。
次に、裂け目の上と下にある「骨組み」を押して近づけることにより、裂け目を傾けていく。
そうして縦のスリットを徐々に横のスリットへ変形すれば、そこに別のフットボールを入れて再び膨らませることができる。
すると、フットボールはもとの配置から「反転」したことになる。
それを数学的に正確な方法でおこない、ある点で空間を裂き、裂け目を広げ、向きを変え、配置を変えた新たな二次元曲面を挿入して六次元空間に戻せば、最初のものとトポロジー的に異なり、そのため全体の形が異なるカラビ＝ヤウ空間をつくることができる。

　このフロップ転移が数学的に興味深いのは、すでによく知られたトポロジーをもつカラビ＝ヤウからスタートして、見たことのない別のカラビ＝ヤウ空間をつくる方法を教えてくれるからだ。
そのため数学者は、この方法を使うことにより、より多くのカラビ＝ヤウ空間を研究して試すことができる。
フロップ転移は物理的にも何らかの意味があるかもしれない。
カラビ＝ヤウに対して施すことのできる一般的な数学的操作はすべて物理学にも応用できるはずだ。
一般相対論の描像では、滑らかに湾曲した時空が裂けることはないが、アスピンウォール、グリーン、モリソンは、自然界でもフロップ転移のようなものが起こり、空間そのものが裂けることがあるかどうかを知ろうとした。
さらに彼ら三人組は、そのタイプの転移が自然界で起こりうるかどうかを見極めるだけでなく、ひも理論においてそれが起こりうるかどうかも明らかにしようとした。

　そのために三人は、内部に球面をもつカラビ＝ヤウ多様体を取り上げ、それにフロップ転移を施し、得られた（トポロジーが変化した）多様体を使って時空の１０次元のうち６次元をコンパクト化して、どのような四次元物理が得られるかを調べた。
彼らはとくに、ある粒子の質量を予測しようと思い、実際にそれを首尾よく計算した。
続いて同じプロセスを、今度はもとのカラビ＝ヤウ多様体のミラーパートナーを使って繰り返した。
しかしミラーパートナーでは、フロップ転移をおこなっても球面は体積ゼロへ縮まらなかった。
つまり、空間の裂け目ができず、特異点も生じなかった。
次に三人は、同じ粒子　－　今度はミラー多様体に伴う粒子　－　の質量を計算し、結果を比較した。
もし二つの予測が一致すれば、第一のケースにおいて空間が裂けて特異点が生じることは問題にはならず、ひも理論とその基となる幾何学を用いてその状況を連続的に扱えることになる。
計算結果はほぼ完壁に一致し、ひも理論ではこの種の裂け目が生じても悲惨な結果にならないことが示された。

　三人の解析において答えが出なかった一つの問題が、どうしてそうなるのか、つまり、ひもの大きさが許容される最小のサイズであるのに、どうやってたとえば球面が体積ゼロ（従来の幾何学における点のサイズ）に縮むのかということだ。
その答えかもしれないものが、同時に発表されたウィッテンの論文に含まれていた。
そこには、ひものループで空間の裂け目を取り囲み、起こりうる災難から宇宙を守る方法が示されていた。

　アスピンウォールは次のように説明する。
「カラビ＝ヤウの古典幾何が特異的であるように思えたとしても、その四次元の物理は滑らかに見えることがわかった。粒子の質量は無限大に発散せず、まずいことは何も起こらない」。
ひも理論の量子幾何は何らかの「平滑効果」をもっており、古典幾何学では特異的に見えるものを非特異的にするに違いない。

　フロップ転移は、古典幾何学では扱えないような状況を指摘することにより、量子幾何学がどのようなものであるかという問題に光を当ててくれるかもしれない。
古典幾何学は、フロップの最初と最後の状況は問題なく記述できるが、バスケットボールの幅がゼロに縮む中間段階ではうまくいかない。
このケースを含め、見つけられる限りのできるだけ多くのケースにおいて、ひも理論がどの点で異なるかを正確に調べることにより、古典幾何学をどのように修正すべきか、つまりどのような種類の量子補正が必要なのかを明らかにできる。

　次に来る疑問は、「幾何に施さなければならないその量子補正は、やはり幾何と呼べるほどに幾何学的に見えるのか、あるいは大きく異なっており、幾何という概念を完全に放棄しなければならないのかだ」。
フロップ転移などの例を通じていまのところわかっている量子補正は、「簡単には計算できないかもしれないが、やはり幾何学的に記述できる」とモリソンは言う。
しかし、それが一般的に成り立つかどうかはまだわかっていない。

　未来に目を向けると、量子幾何学の理論の構築は、数学全体とまでは言わないものの、幾何学の分野が直面する最大の挑戦の一つであることは明らかだ。
それは何十年にも及ぶ試練であり、物理学者と数学者の密接な協力を必要とするだろう。
その課題においては、私たちが常に心がけている数学的厳密さがもちろん必要だが、私たち数学者を驚かせつづけている物理学者の直観も同じくらい役に立つかもしれない。

　宇宙の内部次元の幾何を理解することは、次元そのものは小さいかもしれないが、間違いなく大きな問題だ。