拡張標準モデルとは？

　時空の基本的な対称性にはローレンツ対称性とは別に「CPT対称性」というものがあり、これも相対論が破れた場合には保たれなくなる可能性がある。
CPT対称性は
①粒子と反粒子を置き換える（電荷Cの反転）
②粒子を鏡像関係にある粒子に置き換える（パリティPの反転）
③時間Tの反転
という3つの変換を同時に行っても、物理法則が変わらないという性質である。標準モデルではCPT対称性が保たれるが、相対論の破れを認めるような理論ではこれが破れるかもしれない。

究極理論では相対論の破れがどんな形で現れてくるのだろうか？ 最も無理がなく明快な形としては、「ローレンツ対称性の自発的破れ」と呼ばれるものが考えられる。「対称性の自発的破れ」とは、物理法則そのものは対称なのに、実際の系では対称性が破れることをいう。こうした例はいくつも知られており、ローレンツ対称性についても自発的破れが考えられる。

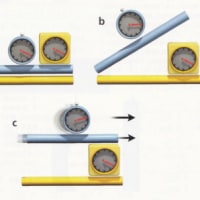
　たとえ話を用いて説明しよう。細い円筒形の棒を床の上に垂直に立てて、上から力を加えたとする（下図参照）。この状態は棒を中心軸とした回転に対して完全に対称である。棒は円筒形であり、力は上下方向に働いている。
このため、この状態を表現する物理学の数式も回転に対して対称である。しかし力が強くなると、やがて棒はいずれかの方向に曲がり、回転対称性が自発的に破れる。

上左図：対称性の自発的な破れ
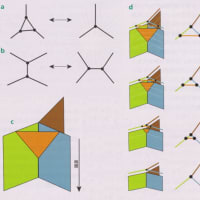
ある系の条件が完全に対称で、その状態を記述する方程式も対称であるにもかかわらず非対称な結果が現れることを「対称性の自発的な破れ」という。例えば円筒形の棒を立てて、垂直な力を加えた場合を考えてみよう（左）。この系は棒の中心を軸とする回転に関して完全に対称である。しかし、加わる力が十分に大きくなると系は不安定になリ、棒はいずれかの方向に曲がってしまう（右）。この対称性の破れは、棒がどの方向にどれだけ曲がったかを示すベクトル（赤の矢印）で表現できる。これと似たベクトル量が時空全体に生じることが、 ローレンツ対称性の破れを引き起こす。
上右図：地球が回ると実験室も回る。
インディアナ大学の実験室（黄色の点）も例外ではない。相対論の破れをもたらすベクトル場（矢印）は時空をくまなく満たしておリ、実験室はこのベクトル場に対しても回転することになる。実験室を基準とすると、ベクトル場の方向は1日を通して少しずつ変化するように見える。このため、ローレンツ対称性の破れを検出する実験が可能になる。実験室に質量の異なる2つの物体を置いておくと、質量が周期的にわずかに変化するのが観測できるだろう。

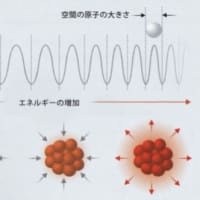
　このたとえを相対論の例に当てはめると、棒と力を記述する数式が究極理論の方程式にあたり、棒は物質や力の量子場に相当する。通常、これらの場の大きさはゼロだが、ある状況ではゼロではなくなる（このような場を「背景場」と呼ぶ）。電場についてこのような現象が起きたとしよう。電場は方向を持った量（ベクトルと呼ぶ）なので、これに応じて空間のあらゆる位置について方向が定まる。電荷を帯びた粒子が存在すれば、電場の方向に加速されるだろう。こうして回転対称性が破れる（ブースト対称性も破れる）。同様の理屈は大きさがゼロではないすべての「テンソル場」に当てはまる。ベクトルはテンソルの特殊な場合である。

　標準モデルでは、ゼロでないテンソル場が自発的に生じることはない。だが、ひも理論をはじめとするいくつかの基礎理論では、ローレンツ対称性の自発的破れが起こる余地がある。A.コスレテツキーとサミュエルは、ひも理論や重力を含む場の理論に基づくと、ローレンツ対称性が自発的に破れて相対論の破れを観測できる可能性があることを1989年に初めて指摘した。

　その後、コスレテツキーはポティングとともにこの考えを拡張し、ひも理論ではCPT対称性も自発的に破れうることを1991年に示した。それ以降、ひも理論や他の量子重力理論の中で、相対論の破れをもたらすメカニズムがいくつも提案されている。

　もし究極理論の枠組みの中でローレンツ対称性の自発的破れなどのメカニズムが実際に働くなら、それに伴って生じる相対論の破れを実験的に確認し、究極理論の正しさを示す初の証拠が得られるだろう。

　標準モデルの拡張版、究極理論では何らかのメカニズムによってローレンツ対称性が破れ、おそらくはCPT対称性も破れるものとすると、どんな実験をすればそれを観測できるだろうか。また、対称性の破れは従来の物理学とどう関連するのか？

　これらの疑問に答えるには、起こりうるすべての効果を包含し、あらゆる実験結果の分析に適用できる包括的な理論的枠組みが欲しいところである。それがあれば、実験結果に基づいて特定のパラメーターを計算したり、異なる実験を比較したり、対称性の破れがもたらす効果を予言できるようになる。

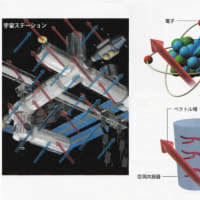
図：軌道上の実験室＿宇宙で探る時空の性質
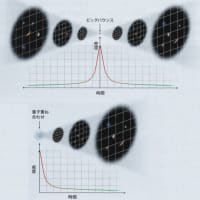
ローレンツ対称性の破れを探るため、将来は国際宇宙ステーションなどの人工衛星の上で時計の進み具合を比較する実験が行われるだろう。図では相対論の破れを引き起こす2種類のベクトル場を赤と青の矢印で表している。これらのベクトル場はそれぞれ異なる形で粒子と相互作用する。上の図は原子時計（原子として図示）と、空洞共振器内の光やマイク口波を利用した時計を比較した例。光と電子（赤）は赤のベクトルと相互作用し、陽子（青）は青のベクトルと相互作用する。
宇宙ステーションが回転するにつれ、時計とベクトル場の方向関係が変わリ、ベクトル場との相互作用が変化して2つの時計にズレが生じるだろう。これがローレンツ対称性の破れの証拠となる。国際宇宙ステーションは92分周期で地球を周回しているので、地上の実験室よりも高精度のデータをはるかに短時間で得られる。

　そうした理論的枠組みを構築するうえで、基本となる事柄がある。第1に、どんな物理現象も特定の時空座標系に依存してはならないこと。第2に、これまで標準モデルと一般相対性理論が実験事実にうまく合致していることから、ローレンツ対称性とCPT対称性が破れているとしても、その破れはごく小さいに違いない。

　これらの基本条件を満たし、力と粒子は既知のものしか存在しないとすると、方程式に付け加えうる項（つまり、考えられる相互作用）はおのずと限られてくる。これらの項はそれぞれ、大きさがゼロではないテンソル場の存在に対応する。各項がどのくらい強く影響するかは項にかかる係数によって決まるが、係数の値は不明である。もっとも、究極理論が明らかになれば、係数の多くはゼロだと判明するだろう。

　こうして得られたのが、拡張した標準モデルと呼ばれる理論である。この理論の優れたところは非常に一般性があるという点である。相対論の破れの起源を哲学的・物理学的にどう考えるかによらず、その結果は必ず拡張標準モデル（SME)で記述されることになる。なぜなら、拡張標準モデルは相対論に関して考えうる妥当な修正や一般化をすべて包含した枠組みであり、しかも従来の標準モデルや重力についての事実と整合性が取れた理論だからである。

　ローレンツ対称性の破れの効果をイメージするには、時空が本来、方向を備えた存在であると考えるのがよい。拡張標準モデルの場合、ベクトル場は方程式の特定の項に対応し、このベクトル場の方向が時空の方向と一致する。より一般的なテンソル場についても同様だが、もう少し複雑になる。

　粒子はこれらの背景場から影響を受けるため、粒子の運動や粒子間の相互作用は方向に依存するようになる。電場や磁場の中で動く荷電粒子が特定の方向に影響を受けるのと似たようなものである。CPT対称性の破れも同じようにイメージできる。ただしこの場合は、背景場との結びつきが粒子と反粒子で異なることが原因で影響が表れる。

　拡張標準モデルによると、相対論の破れに伴って粒子の振る舞いがさまざまな形で影響を受けると予想される。粒子の性質と相互作用はその運動方向に応じて変わる可能性があり（回転対称性の破れ）、運動の速さにも依存するとみられる（ブースト対称性の破れ）。粒子がスピン（固有の角運動量）を持っている場合には、スピンの大きさと方向によって、相対論の破れが異なると考えられる。また、粒子が自身の反粒子と同じ性質を持たない可能性もある。さらに、粒子の種類によってこれらの影響の程度が異なっている可能性がある。例えば陽子には中性子よりも大きな影響が生じ、電子はまるで影響を受けないかもしれない。

　これらの効果を組み合わせると、実験によって検出可能な興味深い現象がいろいろ考えられる。すでにそうした検出実験がいくつか始まっている。ただし、いまのところ相対論の破れを示す決定的証拠は見つかっていない。