私たちの暮らしているこの地球は太陽系に属しています。
しかしこの太陽系は、我々が現在の宇宙物理学でいうところの太陽系とはかなり異なった形体をしていることはここのブログで何度も述べてきました。
もう一度その概略を整理してみましょう。
そ の大前提と考えなくてはならないことは、私たち人類が認識しているこの地球は、囲われた(シールドされた)時空間に存在する太陽系に属する地球という惑星 に住む存在としての人類なのです。そして、そのシールドされた太陽系の大きさが、我々の宇宙論では直径10万光年の天の川銀河系という大きさに対応してい ます。だから、この銀河系と称している場の中には太陽系以外のものは何も存在しません。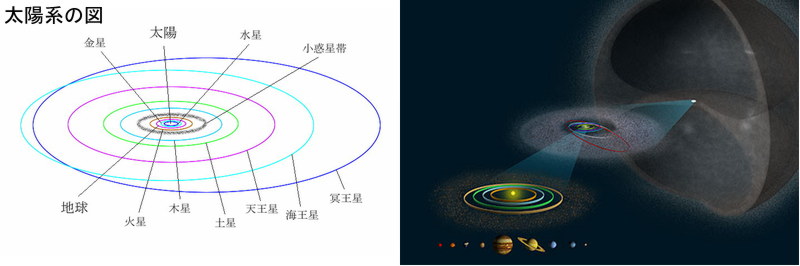
上図左は冥王星の軌道までを表した惑星配置図です。上右図はカイパーベルト帯(最も奥にある暗い球体の中心の白い点)を含めた巨大球体でシールドされた空間配置図です。そして、この暗黒球体の大きさが直径10万光年の太陽系の大きさとなります(想像図)。
私たちはたとえ閉じ込められているとしても、その外には私たちの太陽系(天の川銀河)を含む銀河系があり、その銀河星雲を包括する銀河団があり、またその銀河団を構造体とする大規模構造の宇宙があります。
そしてそれをオーム宇宙ということにします。また、この「存在」の中にはこのオーム宇宙のような宇宙が数限りなくあります。
私 たち人間は何らかの理由でその中に閉じ込められ、その中である一定の水準に達するまで地球という惑星の中で学びを求められている存在でもあります。リザム の等式やリザムの宇宙で述べていますように、地球という惑星は太陽系も含めて私たちが想像するよりもかなり特殊な存在です。
以上のように、この無限とも思える「オーム宇宙」の中には私たちと同じような学びをする惑星が私たちを含めて9個あります(今の地球は2回目の学びの時で。全体では10回目の学びの惑星です)。
さて、ここで我々「人類に課せられた難問」となるのですが、それはこの宇宙で物質体であるという存在はこの9個の惑星だけなのです。さっきも述べましたように、この太陽系に課せられた諸惑星は想像を絶するような「特殊な存在」なのです。
私 たちが夜空の星を眺めて、あるいは天文学者なら望遠鏡で太陽系外の星を観測して、それを地球にある物質と同じ元素記号(H,C,N,O・・・)で出来た 「物」だと信じ、しかも本当であるように思い込むことで科学を発展させて来ましたが、それは間違いの科学認識で創造されたものです。
この宇宙で私たちが「物質」と認識している「物」と、ほとんど同じ状態(物質)で存在する星(惑星)は、9個しかないのです(つまりほとんどゼロに近いのです)。
それでは、あの夜空に見える星々は一体何なのでしょうか。
このことを解明するためには、まずは「物質」についての認識を深める必要が有りそうです。そして、この物質について追及することは、時空構造(時間と空間の認識)や次元についても知る必要が出てきます。
ここのブログでは、物質が存在するための空間三次元と時間としての一次元についてリザムの宇宙図で詳しく説明してきました。ただ、この宇宙図だけで空間認識をするためには、それだけでも一般常識と違いすぎているために、大変な苦労をする必要があります。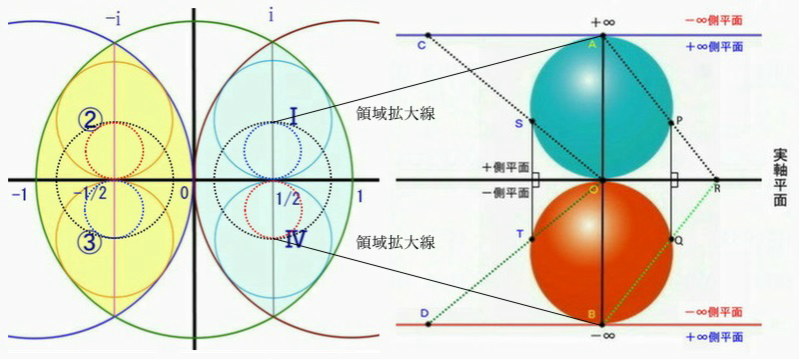
上の右図では赤と青の球体部分が直径10万光年の太陽系に相当します。しかし現代天文学で観測している物質としての宇宙は青い球体の部分だけということになります。当然赤い球体は鏡に映った宇宙のような存在です。
また、上の左図から推測できますように青色領域が上右図ですから、黄色領域は我々の銀河系(太陽系)とは異なる兄弟の銀河系(例えばアンドロメダ銀河)として認識できるのかもしれません。
し かし、今回の記事は、この「3+1」次元の時空構造とは異なった、精神世界でいうところの高次元波動を認識するしか方法が無いようです。しかもこの高次元 波動にはフラクタル次元、例えば3.2次元・1.4π次元・√5次元・・・といったような、整数次元では表せない次元構造を想定する必要性があります。
まずは最低限の「物質」の説明をしておきます。そしてそれから高次元波動(ここでは地球霊界の構造)の説明に入りたいと思っています。
次回は、地球霊界の構造も含めた「物質」について述べる予定です。
レベル1から3までのマルチバースでは、初期条件や物理定数はそれぞれ異なりうるものの、自然を支配する基本法則は同じである。しかし、そこで打ち止めにする必要があるだろうか。
自然法則そのものが違う宇宙があってもよいのではないか。量子効果が存在せず、古典物理学の法則に従う宇宙などというのはどうだろう。時間が連続したものではなく、コンピューターのクロック信号のように離散的なステップを踏んでやってくる宇宙なんていかがだろうか。何もない空っぽの12面体の宇宙というのもありかもしれない。レベル4マルチバースでは、これらすべてが実在する。このてのマルチバースの存在が予想されるのは、抽象的な理論の世界と観測された実世界との間に厳密な対応関係があるためである。
私たちの世界は数式、より一般的には数やベクトル、幾何学図形といった数理的構造によって非常な迫真性をもって記述できる。物理学者のウィグナーが1959年に行った有名な講義の中で、「自然科学において数学が桁外れの実用性を発揮しているのは、ある種の神秘といえる」と語った。裏返していえば、数理的構造が得体の知れない現実感を伴っているということである。
数理的構造は客観的な存在であり、誰が研究しても同じ結論になるという客観的存在としての条件を満たしている。証明ずみの定理は、それを証明したのが人間であれコンピューターであれ、あるいはお利口なイルカであっても、真実である。思慮深い宇宙人がいるなら、彼らも私たちと同様に同じ数理的構造を見いだすに違いない。数学者たちがふつう数理的構造を「創造した」とはいわず、「発見した」と表現するのもこのためである。
数学と物理学との対応関係をどう理解するかについては、2つのパラダイムがある。いずれももっともだが、まったく相反する見方で、おそらくプラトンとアリストテレスの時代から意見が分かれてきたであろう。
アリストテレス哲学の見方によれば、根本は物理的実体であって、数学的表現は単なる便利な近似にすぎない。一方のプラトン哲学によると、数理的構造こそが真の実体であり、観測者はそれを不完全な形でしか認識できない。これらは、どちらの視点がより基本的なのか、観測者という“蛙の視点”と物理法則という“鳥の視点”のどちらを基本的と見るかの違いである。アリストテレスは蛙の視点を、プラトンは鳥の視点を重視する。
私たちはみな、数学について何も知らない子どものころに、アリストテレス的な見方に慣らされている。プラトン的な見方は後に身につくものである。しかし、現代の物理学者たちはプラトン的見方に傾いている。数学によって宇宙をこれほどうまく記述できるのは、宇宙そのものが本来、数理的であると考えられるためである。
とすると、あらゆる物理現象は詰まるところ数学の問題だということになる。無限の知力と力量を持つ数学者がいたなら、原理的には“蛙の視点”を計算できるだろう。その宇宙が内に含んでいる自意識を持つ観測者とは何なのか、その観測者が何を認識しているのか、彼らが認識内容を他者に伝えるためにどんな言語を考案するか、といった事柄までも計算できるだろう。
数理的構造は不変の抽象的実在であり、空間や時間に縛られない。もし歴史が映画のようなものなら、その構造は映画のワンシーンではなく、一巻のビデオテープに相当する。
ここで、3次元空間の中を動き回る点のような粒子でできあがっている宇宙を考えてみよう。4次元時空の中では(鳥の視点に立てば)、これらの粒了の軌跡はもつれたスパゲティのように見える。蛙からは粒子が等速運動して見える場合、鳥の視点からはゆでる前のスパゲティのような1本の真っ直ぐな軌道が見える。蛙からは2個の粒子が対になって回転して見える場合、鳥に見えるのは二重らせんのようにもつれ合う2本のスパゲティとして見える。
蛙にとっては、世界はニュートンの運動方程式と万有引力の法則によって記述される。しかし、鳥にとっては、スパゲティの幾何学的配置、つまり1つの数理的構造が世界の記述となる。蛙そのものもゴチャゴチャした一塊のパスタにすぎず、その非常に複雑な絡み合いが情報を蓄積・処理する生体としての粒子集団を表している。私たちの宇宙はこの例よりもはるかに複雑で、どのような数理的構造が対応しているのかはまだわかっていない。
さて、プラトン的パラダイムに立つと、「宇宙が現在のような宇宙になったのはなぜか」という疑問が持ち上がる。アリストテレス学派にとっては、これは意味のない問いである。宇宙は現に存在するものでしかない。しかし、プラトン学派の立場からは、宇宙がいまとは違う宇宙にならなかったのはなぜかと問わずにはいられない。宇宙が数理的なものなら、多くの数理的構造からどうして特定の1つだけが選ばれ、宇宙を記述するようになったのかは、実存の最も本質的なところに、基本的な非対称性が組み込まれているように思えてしまう。
この難問を回避するため、数理的な対称性は完全に保たれ、あらゆる数理的構造が物理的にも存在するものと考える。それぞれの数理的構造が宇宙に対応し、全体としてマルチバースを形作る。このマルチバースを構成する個々の要素は同じ空間には存在せず、空間と時間を超えた存在となる。おそらく、内部に観測者を含まない宇宙が大半であろう。
この仮説はプラトン的な考え方を究極にまで突き詰めたものといえる。プラトンのイデアの世界にある数理的構造、あるいは数学者ラッカーのいう「マインドスケープ」が物理的にも存在するというわけである。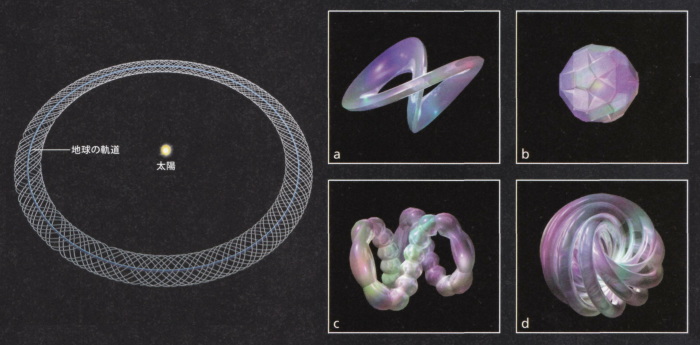
図:数理的構造そのものが宇宙「レベル4マルチバース」
究極の並行宇宙はあらゆる可能性を含む。その位置や宇宙論的な特性、量子状態が異なるだけでなく、物理法則までが異なる宇宙の存在が考えられる。これらの宇宙は空間と時間を超えたところにあるので、目に見えるように描くのはまず不可能である。最良の方法は、抽象的に思い描くこと。宇宙とは、それを支配する物理法則の数理的構造を表現した「彫刻」のようなものといえる。例えば、1つの単純な宇宙を考えよう。地球と月、太陽があり、ニュートン力学に従っているとする。客観的立場の観測者からは、この宇宙は組み紐で覆われた丸い輪のように見える(丸い輪は地球の軌跡、それを覆う組み紐は地球を周回する月の軌跡)。物理法則が異なれば、宇宙の形も異なってくる(a~d)。この考え方に立つと、物理学の根本にかかわるさまざまな問題が解決する。
マルチバースの階層構造はレベル4でおしまいになる。基礎的な物理理論が自己矛盾のないものならば、これらはいずれも何らかの数理的構造によって表現可能だからである。
レベル4マルチバースの仮説は実証可能であり、レベル2マルチバースの場合と同様、レベル4マルチバースは1つの集合(この場合は数理的構造の全体)と選択効果を含んでいる。数理的構造の分類が進むにつれ、私たちの世界を記述している数理的構造が観測結果と一致する最も一般的な構造であることが判明するだろう。同様に、私たちが将来に観測する事柄は過去の観測事実と首尾一貫した一般的なものになるはずで、過去の観測事実は私たちの存在と矛盾しない最も一般的なものである。
「一般的」が何を意味するかを定量的に示すのは難しい問題で、その研究は緒についたばかりである。しかし、数理的構造には1つの顕著で有望な特徴がある。私たちの宇宙が明快で秩序を持っているのは数理的構造の対称性と不変性のおかげであるが、これらは例外なく一般的だという点である。数理的構造にはもともとこうした特徴が備わっているようで、この特徴を取り除くには複雑な公理を付け加える必要がある。
ここまで紹介してきたように並行宇宙には4つの階層があり、レベル1からレベル4へと向かうにつれて私たちの宇宙とはかけ離れたものになる。レベル1では宇宙の初期条件が異なるだけだが、レベル2では物理定数や粒子にも差が生じ、レベル4に至っては物理法則そのものが異なる余地がある。私たちの宇宙と質的に変わりがないのはレベル3だけで、過去数十年にわたってレベル3宇宙の考え方が反論の嵐に見舞われてきたのは皮肉なことである。
今後数年で、宇宙マイクロ波背景放射や大規模スケールでの物質分布など宇宙論に関連する観測が劇的に進むとみられ、空間の曲率と位相幾何学的性質がもっと正確に突き止められることにより、レベル1宇宙の仮説に白黒がつくだろう。こうした観測を通じてカオス的永久インフレーション理論を検証することにより、レベル2宇宙を調べることもできるだろう。宇宙物理学と高エネルギー物理学の双方が進歩すれば、物理定数がどの程度まで微調整されたかが明確になり、レベル2宇宙が存在するのかしないのか、可能性が絞り込まれてくるはずである。
量子コンピューターの研究開発が実を結べば、レベル3宇宙の新たな存在証明となる。量子コンピューターは基本的に、並列計算にレベル3宇宙の並行性を利用するものだからである。一方では「ユニタリー性の破れ」を探す実験も進みつつあり、もしもこの証拠がつかめた場合、レベル3宇宙は存在しないことになる。
そして最終的には、一般相対性理論と場の量子論の統合という現代物理学最大の難問が解決されるかどうかで、レベル4宇宙に対する見方が大きく左右される。私たちの宇宙に厳密にマッチする数理的構造が見つかるか、あるいは数学的に理不尽な壁にぶつかってこの仮説を放棄せざるをえなくなるかのいずれかとなる。
だから、私たちも並行宇宙の存在を信じてみてはいかがだろうか。これに対し、並行宇宙に関する議論は何の役にも立たないうえ、いかにも奇妙すぎるという反論もある。決して観測できない世界を仮定するなど、「オッカムのかみそり」(「最も単純な説明が最良である場合が多い」とする原則)に照らしても説得力を欠く。異なる世界が無限に存在するほど、自然は浪費家ではないはずである。
しかし、この議論は裏を返すと、マルチバースの存在を支持することにもなりうる。自然が本当に浪費しているのは何だろう。空間や質量、原子などではないのは確かである。レベル1マルチバースにしても、すでにこれらを無限に含んでいるのだから、そのほかに少しくらい無駄にするものがあっても何の問題にもならない。重要なのは、単純明快さが損なわれるかどうかである。
全体集合はしばしばその構成要素よりも単純な場合がある。例えば整数全体の集合を考えよう。全集合と1つの数字のどちらが単純だろうか。素朴に考えると、数字1つのほうが単純に思える。しかし、整数全体を生成するコンピュータープログラムはとても簡単で、これに比べると大きな数1つを記述するほうがずっと長い行数を占めることもある。実は全体のほうが単純なのである。
同様に、アインシュタインの場の方程式に対する解の全体集合は、個々の解よりも単純で、一般解はいくつかの方程式で表現できるが、個々の解を求めるには、ある超曲面上での膨大な初期値を特定する必要がある。つまり、集合の中の特定の要素に関心を絞ると複雑さが増し、すべての要素をまとめ上げていた全体性に本来備わっていた対称性や単純さが損なわれてしまうということである。
この意味では、高レベルのマルチバースほど単純である。私たちの宇宙に比べ、レベル1マルチバースは特別な初期条件を設定する必要がないという点で単純である。そして、レベル2では物理定数を特定する必要もなくなり、レベル4になると一切を特定しなくてよくなる。一見すると豊かな複雑さも、すべては観測者(蛙の視点)が主観的に認識するものの中にある。鳥の視点に立てば、マルチバースほど単純なものはない。
マルチバースの概念が奇妙すぎるという不満は、科学というよりは美意識の問題だろうし、そもそもアリストテレス的世界観に立った場合だけに問題となるものである。奇妙だからといって、では何だというのだろうか。実在の本質に迫る深遠な問いに対する答えが、奇妙なものではないとでもいうのだろうか。私たちは遠い祖先から今日に至るまで、日常の物理現象に関する直観を育んできた。進化の過程で、それが生存競争に有利だったからである。逆にいえば、日常世界をひとたび離れれば、奇妙に見える事柄を予測するほうがむしろ当然といえよう。
4つのマルチバースに共通する特徴は、並行宇宙に本来備わっている単純さと、おそらくはこれ以上明快なものはないといえるほど鮮やかな理論である。これら宇宙の存在を否定するには、実験的に確かめられていないプロセスや場当たり的な仮定を加えるなどして、理論を複雑にしなくてはならない。例えば、空間が有限であるとか、波動関数が収縮するとか、存在論的な非対称性などを持ち込まねばならなくなる。
結局のところ、無駄であか抜けしないのはどちらなのかという判断になる。たくさんの世界と、たくさんの論争のどちらを選ぶかである。おそらく私たちは、私たちの宇宙が奇妙であることにだんだんと慣れ、その奇妙さが魅力の一部であることに気づくだろう。
レベル1と2のマルチバースは天文学者も手が届かないような遠く離れた並行宇宙だった。これに対し、レベル3のマルチバースは私たちのすぐそばにある。そしてそれは、量子力学の「多世界解釈」から生じるマルチ世界である。多世界解釈では、ランダムな量子過程によって宇宙が複数のコピーに分岐し、そのいずれもが現実になりうると考える。
20世紀初め、量子力学の理論は物理学に革命を起こした。古典的なニュートン力学の法則に従わない原子の世界を説明することに成功したのだ。しかし一方では、量子力学の意味するところをめぐって激論が持ち上がった。
量子力学では粒子の位置や速度といった古典的な事柄に基づいて宇宙の状態を記述するのではなく、波動関数と呼ぶ数学的実体を使って記述する。シュレーディンガー方程式によると、この状態は数学用語で「ユニタリー変換」と呼ぶ様式に従って変化を続ける。これは、ヒルベルト空間という無限次元の抽象的な空間の中で、波動関数が回転するということだ。量子力学的世界は本来がランダムで不確定であると説明されることが多いが、波動関数の変化はランダムでも不確定でもなく、決定論的なものだ。
1920年代の物理学者たちは、対象が観測されると同時に波動関数が古典的な確定状態へ「収縮」すると仮定した(コペンハーゲン解釈)。これによって観測の問題にはうまく説明がついたが、量子力学に本質的な不確定さがつきまとうことはかわらない。
その後、1957年にプリンストン大学のエヴェレットは、量子論によれば古典的実体はさまざまな実体の重ね合わせへと分岐していくが、観測者にとってはこの分岐がわずかなランダムさとなって確率的に見えるにすぎない。その確率が、かつての収縮仮説から導かれる結果とぴったり一致する。こうした古典的世界の重ね合わせがレベル3マルチバース(量子の多重世界)でる。
エヴェレットの多世界解釈は論理的にも最も明解な解釈であるが、専門家にも難解なものとされてきた。しかし、理論を考察するうえで2つの視点があると考えれば理解しやすい。1つは数式を使って研究する物理学者の視点あり、これは鳥が上空から全景を見渡すようなもので、「外部からの眺め」といえる。もう1つは数式が記述する世界の中にいる観測者が見る「内部からの眺め」である。鳥とは違って、自分自身が風景の中にいる蛙の立場に例えられる。
鳥の視点から見たレベル3マルチバースは単純で、ただ1つの波動関数が見えるだけである。この波動関数が時とともに穏やかに、しかも決定論的に変化していく。分裂したり併存したりはしない。波動関数の変化によって記述される抽象的な量子世界は、その内部に古典物理学では記述できない多くの量子現象を含むのことはもちろん、古典的な事象の系列をたくさん含んでいる。そして、どんな事象が起きるのかという“物語の筋”が分裂と融合を繰り返す。
一方、蛙の視点からは、こうした全体像のごく一部しか認識できない。自分がいるレベル1宇宙が見えるだけである。レベル3並行宇宙にいる自分のコピーは、「量子デコヒーレンス」という過程のせいで見えなくなってしまう。量子デコヒーレンスとは、量子系の干渉が環境との相互作用によって失われる現象で、波動関数がユニタリー性を保ちつつ収縮する過程と同じである。
観測者が何らかの判断を下す時には、脳の中で量子効果が働いて結果の重ね合わせ状態が生じる。例えば「この記事を読み続ける」と「読むのをやめる」との重ね合わせだ。ある人が何かを決定するという行為を鳥の視点から眺めると、その人が複数に分裂して見える。記事を読み続ける人と、読むのをやめてしまう人に分かれて見えるのだ。しかし当事者は蛙の視点に立っているので、分裂したもう1人の自分の存在には気がつかず、単なる不確定さとして感じる。読み続けるかどうかは、確率の問題となる。
以上の話は奇妙に思えるかもしれないが、これとまったく同じ状況がレベル1マルチバースの中でも生じる。あなたはこの記事を読み続けると決めてくれたわけだが、遠く離れた銀河にいる「もう1人のあなた」は最初の段落を読んだだけで放り出した。レベル1とレベル3の違いは、「もう1人のあなた」がどこにいるかという点だけである。レベル1の場合は、古き良き3次元空間のどこかにいる。レベル3の場合は、無限次元のヒルベルト空間の中、量子論的に分岐した世界にいる。
レベル3の存在には1つの重大な前提がある。波動関数の時間的変化がユニタリーであるという仮定だ。これまでの実験では、ユニタリー性に反する例は見つかっていない。過去数十年、C60分子や長さ数kmの光ファイバーなど、大きな系でもユニタリー性が確認されてきた。ユニタリー性の問題はデコヒーレンスの発見をきっかけに理論研究も盛んになっている。
量子重力論の理論家たちはユニタリー性を疑問視してきた。ブラックホールの蒸発に伴う情報の破壊は非ユニタリーな過程になるからだ。ブラックホールの事象の地平線近傍で生じる真空のゆらぎのためにブラックホールは黒体放射エネルギーを周りに放出し、しだいに質量を失ってついには消滅する(蒸発)。これに伴い、ブラックホール内に落下した情報も消失してしまうことになる。この情報の消失を避けようという理論的試みも進められている。
しかし最近、ひも理論の研究で画期的な進展があり、「AdS/CFTコレスポンデンス」(負の宇宙定数を持つ反ド・ジッター時空(Ads)と、コンフォーマル変換に対して不変な場の理論(CFT)は相互に対応がつき、同等である)と呼ばれる考え方によって、量子重力もユニタリーであることが示された。だとすると、ブラックホールが情報を破壊することはなく、単にどこか別の場所へ転送しているにすぎない。
物理現象がユニタリーなら、ビッグバン初期に量子ゆらぎがどのように働いたかという標準的な描像を改めねばならない。そうした量子ゆらぎからは無秩序な初期条件は生まれない。むしろ、考えうるすべての初期条件の量子的重ね合わせが生じ、そうした初期条件が同時に併存した。その後、これらがデコヒーレンスによって分岐を起こし、古典的に振る舞うようになった。
量子力学の考え方によると、膨大な数の並行宇宙が存在する。ただし、「それがどこに存在するか」という点については、 解釈を拡張する必要がある。私たちが実感できる通常の空間ではなく、考えうるすべての状態を含む抽象的な領域の中に存在すると考えるのである。世界が取リうるすべての状態、量子力学的な意味での状態)の1つひとつが、異なる宇宙に対応すると考えられるだろう。こうした並行宇宙の存在は、波動の干渉や量子計算といった実験を通じて垣間見ることができる。
あるハッブル体積(レベル3)の中での量子分岐への結果の振り分けは、ある量子分岐(レベル1)の中にあるさまざまなハッブル体積への結果の振り分けとまったく同じである。下の図は、「量子のサイコロ」によって表現した、「エルゴード性」と「時間の本質」を描いたものである。また、量子ゆらぎが持つこの特性は統計力学用語で「エルゴード性」と呼ばれる。
図:レベル3マルチバース
エルゴード性:エルゴード性の原理によると、量子並行宇宙はもっと平凡なタイプの並行宇宙と等価である。1つの量子宇宙はやがて状態が確定した複数の宇宙に分岐する(左)。しかし、こうして新たに生まれた宇宙は、どこか別の空間(右、図ではレベル1マルチバース)にもとから存在していた並行宇宙と変わらない。さまざまな事象がどんな順序で起きるのかを体現したものが並行宇宙だと考えるのがホイントである。この考え方はどんなタイブの並行宇宙にも当てはまる。
時間の本質:普通、時間は変化を記述するための手段と考えられることが多し、物質はある瞬間にある配置を取り、次の瞬間には別の配置になるという具合である(左)、しかし並行宇宙の概念では別の見方ができる。考えうる物質配列が一連の並行宇宙の中にすべて含まれているなら(右)、時間とはこれらの宇宙に順番をつけるやり方にすぎない。個々の宇宙は静的なもので、変化は幻想ということになる。もっとも、この幻想は興味深いものではあるが。
同じ理屈がレベル2にも当てはまる。対称性の破れによって生じる結果は唯一のものではなく、すべての結果の重ね合わせとなり、これが速やかに分岐する。だから、もし物理定数や時空の次元などがレベル3に生じる量子分岐の間で異なるなら、レベル2並行宇宙の間でも同様に異なるだろう。
言い換えると、レベル3マルチバースはレベル1やレベル2となんら変わらない。同じ多数の宇宙が、より見分けにくい形で現れているだけである。別の量子分岐の中で、同じ“物語の筋”が何度も何度も繰り返される。このように考えると、エヴェレットの理論に関して巻き起こった議論も、比較的議論の少ないマルチバース(レベル1と2)の考え方によってあっけなく終息するように思える。
レベル3マルチバースが意味するところは深遠で、物理学者たちはその意味を探り始めたばかりである。例えば“物語の筋”が分裂するなら、「宇宙の数は時とともに指数関数的に増えていくのか」という疑問がある。意外なことに、答えは「ノー」である。
鳥の視点からは、もちろん1つの量子宇宙が見える。蛙の視点からは、その瞬間に区別可能な宇宙の数が問題になる。惑星の位置が異なっている宇宙や、あなたが誰か別の人と結婚しているような宇宙などである。量子レベルでは、温度が10^8K以下なら10の10^118乗個の宇宙が存在する。これは膨大な数ではあるが、有限である。
蛙の視点では、波動関数の変化はこれら10の10^118乗個の状態の1つから別の1つへと移る果てしない流転に相当する。いま、あなたは宇宙Aにいて、この文を読んでいる。しかし、次の瞬間には別の宇宙Bに移り、いま現在は宇宙Aにいた場合とは別のこの文を読んでいる。宇宙Aも宇宙Bも同一の観測者を含んでいるのだが、宇宙Bにいる観測者のほうが少しだけ記憶が多い。
存在しうるすべての状態があらゆる瞬間ごとに存在し、時間の経過はそれを観察することによって実感されるのかもしれない。この考え方はイーガンが1994年に著したSF小説『順列都市』に見られるほか、英オックスフオード大学の物理学者ドイチュや独立の物理学者バーバーらが発展させたものである。このように、並行宇宙の考え方は時間の本質を理解するうえでも不可欠となるだろう。
さて、次はさまざまなレベル1マルチバースが集まった無限集合を下の図1に示す。個々のレベル1マルチバースを比較すると、時空の次元や物理定数の値が異なっている場合もある。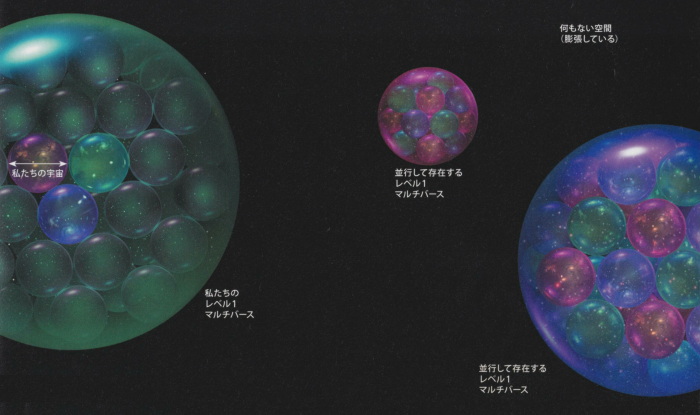
図1:レベル2マルチバース
インフレーション理論からは、レベル1よりもやや精巧な別種の並行宇宙の存在が浮かび上がってくる。私たちのレベル1マルチバース(私たちの宇宙とそれに隣接する空間領域)は泡のようなもので、これがより大きな、ほとんど空っぽの空間に埋め込まれているという考え方である。空間の中には別の泡があり、私たちの泡とは切リ離されている。雲の中の水滴のようなイメージである。こうした核ができる際、それぞれの泡では量子場が異なるため、他の泡とは異なった特性が生まれる。
また最近注日のインフレーション理論の改良版の一つで、もともと空間は真空のエネルギーの高い状態にあり、いたるところでこの真空のエネルギーがカオティックに転げ落ちることで多くの宇宙が作られるとした「カオス的永久インフレーション理論」は、こうしたマルチバースの存在を予言している。
この理論は、落下の遅い場所の空間はインフレーションを続けてどんどん体積も増えるので、全空間の真空のエネルギーが落下して消えることはない。したがって、大きな空間スケールで見ればインフレーションは永遠に続き、そこから常に新たな宇宙が作られ続けるとする理論である。これらマルチバースの集合体が「レベル2マルチバース」を形作ることになる。
インフレーション理論はビッグバン理論を拡張したもので、宇宙がなぜこんなにも大きく、均一で平坦なのかなど、ビッグバン理論では未解決だった問題に決着をつける考え方である。宇宙誕生の際に空間が急激に広がったとすると、こうした問題に一挙に説明がつく。空間の急拡大は素粒子の理論などから予言され、これを支持する証拠も得られている。
「カオス的永久」という形容は、非常に大きなスケールで生じる出来事を指している。空間は全体として永久に膨張を続けるが、その中のいくつかの領域は拡大をやめ、個別に「泡」のような構造を作る。発酵して膨らんだパン生地の中に気泡ができるのに似ている(図2参照)。こうして無数の泡ができ、それぞれがレベル1マルチバースの“タネ”になる。泡の大きさは無限で、物質によって満たされている。物質はインフレーションの原動力となったエネルギー場によって生じたものである。
図2:泡の生成
ある種の量子(インフラトン)の場が空間の急激な膨張を引き起こす。空間の中では、ランダムなゆらぎが存在し、この量子場はなかなか消えずに残る。しかし、ある領域では量子場が弱まり、膨張が緩やかになる。こうした領域が泡になる。
これらの泡は、地球から光の速度で旅しても永久にたどり着けないという意味で、“無限の彼方”にある。泡と泡の間の空間が急速に広がり、私たちがいかに速く旅しようとも追いつかないからだ。私たちの子孫も、他のレベル2マルチバースに住む「もう1人の自分」を見ることはできない。また同様の理由で、レベル1マルチバースでも膨張が加速しているなら、「もう1人の自分」を見ることはやはり不可能になるだろう(最近の観測結果は宇宙膨張の加速を裏付けている)。
レベル2マルチバースはレベル1よりもずっと多様だ。それぞれの泡は初期条件が異なるだけでなく、常識的には不変に思える自然の本質までもが異なっている。
現代の物理学では、時空の次元や基本粒子の性質、数々の物理定数などが物理法則に組み込まれているのではなく、「対称性の破れ」と呼ばれる過程の結果として生じたと考えるのが一般的である。例えば私たちの宇宙にはかつて9つの空間次元があり、それらは対等の関係にあったと考えられている。宇宙のごく初期に、うち3つの次元が宇宙とともに膨張し、いま私たちが見ているような3次元空間になった。残り6つの次元は現在では観測できない。これらがドーナツ形の位相構造として極微の世界にとどまっているか、9次元空間中の3次元の膜(ブレーン)にすべての物質が閉じ込められてしまったかのどちらかだ。
このように、複数な次元の間に存在していた本来の対称性が破れた。カオス的インフレーションを引き起こした量子ゆらぎが原因で対称性が破れたのだが、このゆらぎが泡によって異なったとすれば、対称性の破れ方も異なった可能性がある。ある泡では空間が4次元となり、別の泡は3世代ではなく2世代のクォークしか含まず、またあるものは私たちの宇宙よりも大きな宇宙定数を持っているのかもしれない。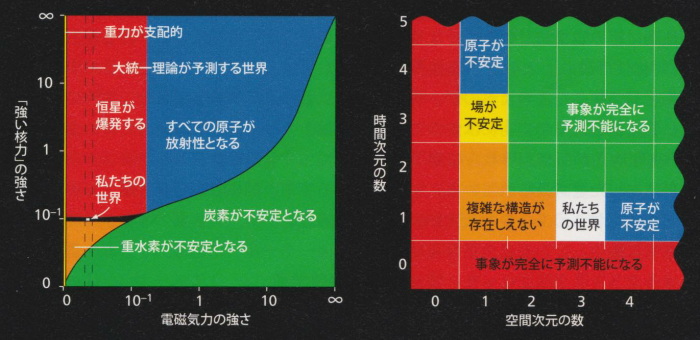
図3:レベル2マルチバースが存在する証拠?
宇宙論研究者たちは私たちの宇宙の特性を精査した結果、レベル2マルチバースが存在すると推論している。根拠となる特性とは、自然界に働く力の強さ(上の左図)や観測される時空次元(上の右図)などである。これらは私たちの宇宙が誕生したときにランダムな過程によって確立したが、結果的には私たち生命が存在しうる値になっている。これはとリもなおさず私たちの宇宙とは異なる値をもつ別の宇宙の存在を示唆している。
レベル2マルチバースの誕生をめぐっては、もう1つ別のシナリオも考えられる。個々の宇宙が生まれ、そして滅びていく循環過程によるという考え方である。スタインハートとテュロックが提唱するモデルによると、私たちの宇宙と文字通り平行な3次元のブレーンがもう1つあり、より高次元の世界の中でこれらが隔てられているにすぎないというものである。
この並行宇宙は私たちの宇宙と相互作用しているので、実は別物とはいえない。しかし、これらブレーン宇宙の集合は1つのマルチバースといえ、おそらくカオス的インフレーションからできる宇宙と同様な多様性を備えているだろう。一方、ペリメター理論物理学研究所のスモーリン はこうしたブレーンではなく、ブラックホールを通じて新たな宇宙が発生し、やはり多様な特質を備えたレベル2マルチバースができるという考え方を提唱している。
マルチバースの考え方が信頼を得るにつれて、物理現象の確率をどう計算するかという厄介な問題が無視できなくなってきた。この問題はレベル1マルチバースではまだ何とかしようがあるが、レベル2ではかなり深刻になり、レベル3、レベル4となると手がつけられなくなる。
多数の観測者が互いに連結していない宇宙に分かれている場合、観測者たちに順番をつける自明な方法はない。ある統計的な重みづけ(数学では「測度」と呼ぶ)によって、 多数の宇宙から抽出するしかない。
例えばタフツ大学のビレンキンらはレベル2マルチバースについてさまざまな宇宙論的パラメーターの確率分布を予測した。多数の宇宙が異なる膨張をし、その体積に比例して可能性が増えると考え、体積の大きな宇宙には統計的に大きな重みを与えた。しかし、無限に大きい宇宙が他よリ2倍の膨張をしたとしても、2 ×∞=∞だから、どちらが大きいかに客観的な意味はない。
さらに、トーラス型の宇宙は体積は有限でも果てはないから、外の視点から見ても内から見ても、無限の体積を持つ周期的な宇宙と同じである。となると、小さな体積の宇宙に対する統計的重みを減らして本当にいいのだろうか? また、レベル2ではなくレベル1マルチバースを考えても、10の10^118乗メートルを超えるとハッブル体積の繰り返しが始まる(周期的ではなく、ランダムにではあるが)。
私たちの宇宙は比較的単純で基本的な数理構造だと考えられるのだから、基本的な対称性の高い宇宙には大きな重みを付けるべきではないのか? さもないと私たちは偶然にも特別な宇宙に住んでいることになってしまう。測度を正しく把握するのはそう単純ではなさそうである。
今の物理学者にできることは、選択効果を考慮に入れながら、何が観測されうるかの確率分布を計算することだけである。その計算結果は、私たちの存在と矛盾するような突飛なものではなく、ありふれたものであるはず?
前回と前々回の2度に渉って、テグマーク が「レベル1マルチバース」という多宇宙について記述してきました。
この「レベル1」とは、約420億光年先の「宇宙の観測地平線(宇宙の地平線)」までは観測できるが、この地平線で宇宙が終わっていると考える理由は特にない。そして、地平線の向こうにも、私たちの周囲と同じような領域が数多く、あるいは無限に存在していてもよいはずで、その各領域では,初期の物質分布は異なっていたかもしれないが、同じ物理法則が支配している。現在,宇宙論研究者の大半はこのタイプの多宇宙解釈を受け入れている。
しかし、一部の研究者はさらに踏み込んで、物理法則や宇宙進化の歴史、さらには時空次元の数さえも違うまったく別の宇宙が存在すると主張する。いくつかの宇宙は生命を宿しているかもしれないが,ほとんどの宇宙は生命が誕生しない不毛の地だろう。この「レベル2」の多宇宙解釈の代表的な支持者はアレックス・ビレンケンである。彼は、「宇宙は無限であると同時に、有限、進化しているのに、静的、永遠でありながら、始まりがある」「私たちの地球とまったく同じ惑星が遠く離れたどこかの領域にあり、そこでは地球と全く同じ惑星が遠く離れたどこかの領域にあり、そこでは地球と同じ海岸線と地勢を持つ大陸があり、私たちのクローンを含めて地球と同じ生き物が住んでいて、その内の何人かはこの本を手に持っている」と、彼の著書、「多世界宇宙の探検(日経)BP社)」の中に書き残している。
この本の「第六章 捨て去るには美しすぎる」に「美しい終了の問題」という箇所があります。ここで真空と水の沸騰をインフレーション理論に結びつけているのですが、やはり、美しすぎるように感じます。少し長くなるかもしれませんが、この第六章の序文を掲載させて戴きます。
・・・・・
どんな物理学者でも、数日前に考えついた美しい理論に致命的な欠点を発見したときの落ち込む感覚を味わっています。悲しいことに、たくさんの美しい理論がこの運命をたどります。インフレーション理論の場合もそうでした。いつものように悪魔はちょっとしたところに潜んでいましいた。詳しく検討してみると、偽の真空は予想していたほどスムーズに崩壊しないのです。
真空が崩壊する過程は水の沸騰によく似ています。真の真空の小さな泡がランダムに出現して、偽真空の真んの中で膨張します(下図)。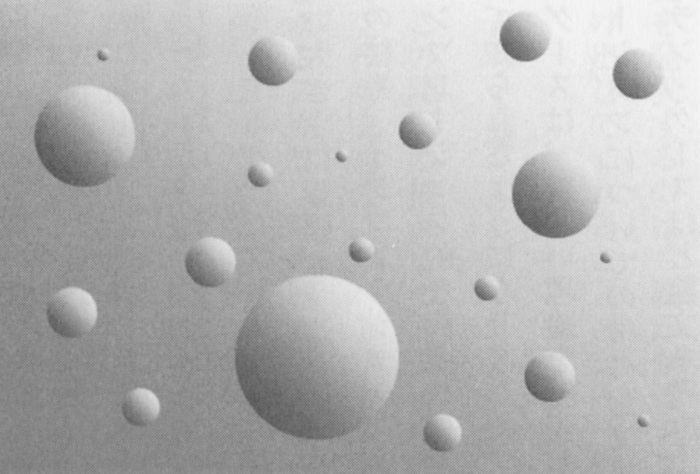
図:真の真空の小さな泡がランダムに勢いよく飛び出して膨張する。先にできた泡の方が大きく成長している。
泡が成長するとき、泡の内部はほとんど空のままです。偽の真空が真の真空に姿を変えることから生まれたすべてのエネルギーは、拡大してゆく泡の壁に集中します。泡同士が衝突してくっつくとき、泡の壁は崩壊して素粒子が放出されます。最終的には、物質の熱い火の玉で満たされた真の真空が姿を現します。
泡がすまじさ割合でい出現すると、こういうことが実際に起こるので、真空が崩壊する過程全体は、「倍増時間」すなわち宇宙の体積が二倍になる時間よりも短い時間で完了してしまうのです。ということは、宇宙が均一で平坦になるよりもはるか以前に、インフレーションはあっという間に終わったということです。反対のケースだったらどうなるでしょうか? 私たちに興味があるのは、反対のケースです。泡形成の割合が低ければ、泡が衝突し始めるときまでに、宇宙は何倍にも膨張することができます。しかし、このケースも難点を抱えているのです。
問題は、泡の間の空間が偽の真空で満たされていて、そのため急速に膨張しているということです。泡は非常に速く膨張し、光速に近い速度ですが、それでさえ偽の真空の指数関数的な膨張には追いつきません。泡が形成された後、宇宙の体積が二倍に膨張するまでの間に泡が衝突しなければ、それ以降泡同士の間隔はどんどん広がる一方で決して衝突しません。
そうするとインフレーションはどうやっても終わらないという結論にいたります。泡は際限ない大きさに膨張し、泡と泡の間の拡大するすき間の中で新しい小さな泡が出現し続けます。その結果、インフレーショにンよって形成される見事な均一性は完全に破壊されてしまいます。インフレーション的な膨張には適切な終り方が欠けているという問題は、「美しい終了の問題」として知られるようになりました。
グースは、新しい理論を発表した二、三か月後に、問題があることに気づきました。インフレーションについての彼の論文は、そのときまだ書かれていませんでした。理由は簡単です。アラン・グースほど論文を書き上げる仕事を先のばしにする人はいないのです(彼との共同研究プロジェクトにたくさん関わってきた私は、すぐにそのことに気づきました)。もちろん、グースは自分の理論に重大な欠点を見つけてがっくりきていました。しかし依然とし彼は、そのアイデアは間違っているとしりぞけるには美しすぎると感じたのでした。一九八〇年の八月にようやく論文に着手したとき、こういう言葉で論文を締めくくっています。「私がこの論文を発表するのは、誰かがインフレーションのシナリオの望ましくない点を取り除く方法を見つけ出してくれることを望み、それを励ましたいからである」。
・・・・・
話が少しそれてしまいましたが、ビレンケンの書籍を紹介した理由は、今回の主題である「レベル2マルチバース」についての考察に、「インフレーションが生む無数の泡宇宙」と非常に深い関係があるからなのです。
私が『多世界宇宙の探検』を読んで、この上の図を見たときの感動(美しさ)が今でも忘れられません。この時、四角形で囲まれた空間(水)がダークエネルギーで満たされた「空」に思えたのです。そして、このエネルギーが水中の1点(特異点)にエネルギーを注入して(ホワイトホール?)気体である水蒸気(私たちの時空構造を持った宇宙)に相転移(インフレーション)を起こし、それがビッグバンとして観測されたのでは?
この様に解釈すると、ホワイトホールから泡が成長するとき、ビレンケンの解釈とは全く逆の宇宙が創造されるのかもしれません。そして、泡の内部(エネルギーを注入して素粒子に満たされた物質宇宙)と泡の壁(ビッグバンの始まり)に対してのエネルギーの流れ方に対する思いを替える必要があるのかも?









