物理学の分野では、近似的記述はよく成り立ち、私たちの宇宙を語るときには、ほぼ完全に記述しているようにみえる。
しかし、プランクスケール(10の-33乗センチメートル)では、標準的な幾何学が量子効果に圧倒され、単純な測定も不可能になるのだ。
きわめて小さいスケールでものを分解するのが困難なのは、ハイゼンベルクの不確定性原理のためで、それにより一個の粒子の位置を特定するのは不可能となっている(ここでは、粒子でなく「点」について論じる)。
プランクスケールでは、すべてのものは静止しておらず、点、距離、曲率を含め揺らいでいるのだ。
隠れた次元や個々のひものレベルで宇宙を探るには、想像しうる最大および最小スケールの両方を扱える新たな種類の幾何学 - 量子幾何学と呼ばれることがある - が必要となるだろう。
その種の幾何学は、大スケールでは一般相対論と、小スケールでは量子力学と、そして二つの理論が収束するところでは両方と相容れなければならない。
このような、大小を扱うことが出来る、量子幾何学の大部分は、まだ存在していない。
重要でありながら推論にすぎず、現実というよりは希望であり、厳密に定義された数学理論の探索につけられた名前でしかない。
そうした理論がどのようなものになるか、何と呼ぶべきか、まったくわかっていない。
幾何学と呼ぶべきかどうかもはっきりしない。
どのような名前にせよ、私たちが知っている幾何学は間違いなく終わりを迎え、私たちの知らないもっと強力な幾何学にとって代わられる。
それがすべての科学のありようで、停滞は死を意味する。
幾何学はアインシュタインの理論と密接に結びついていて、アインシュタインの理論がストレスを受けると、幾何学もストレスを受ける。
ニュートンの方程式がとって代わられたのと同じく、最終的にはアインシュタインの方程式もとって代わられなければならず、幾何学もその道連れになるだろう。
私たちはいつも、科学が破綻する場所を探している。
古典幾何学がプランクスケールで破綻するからといって、その数学自体に何か問題があるわけではない。
プランクスケールは、長さ、質量、時間の物理的スケールであり、このような厄介なことが起こりはじめるプランクスケールは、断じて数学的概念ではない。
一般相対論の基礎であるリーマン幾何学を下支えする微分法が、ある臨界的な長さスケールで突然通用しなくなることはない。
なぜなら、微分幾何学はその前提として、好きなだけゼロに近づけられる無限小の長さにおいて機能するようつくられているからだ。
同様の理由で、一般相対論を最小距離まで外挿することが、数学的観点から問題になるという理由は、物理的観点からも真の問題とはならない。
一般相対論では、計量、すなわち長さの関数から、すべての点における曲率を知ることができる。
しかし、きわめて小さい長さスケールでは計量係数が激しくゆらぎ、それにより長さと曲率も激しくゆらぐ。
つまり、幾何があまりに激しく変化するため、それを幾何と呼んでもほとんど意味をなさないのだ。
その幾何学的な奇妙さも、量子力学と一般相対論が基本的に相容れないことに由来するため、微分幾何学に問題が生じることはない。
量子重力の理論がどのようなものになるにせよ、量子幾何学はその理論の言語 - 量子力学と一般相対論の適合性の問題を解決するのに必要な数学形式 - として考えることができるかもしれない。
この間題について考える方法がもう一つあり、多くの物理学者は、物理学において姿を現す幾何学は基本的なものでなく、「創発」という現象かもしれないと考えている。
もしその見方が正しければ、世界に対する従来の幾何学的記述がきわめて小さくきわめて高エネルギーの領域でつまずくように見える理由を、説明できるかもしれない。
創発現象は、湖や池でも見られる。
かなりの量の水に注目すれば、水は流れることができて波をつくり、粘性、温度、熱勾配といったマクロな特性をもつものと考えて差し支えない。
しかし、きわめて強力な顕微鏡で微小な水滴を調べると、流体とは似ても似つかない。
誰もが知っているように、水は分子からできており、小スケールでは、液体というよりもビリヤードのボールのように振る舞う。
「池の水面の波を見て、そこからH2Oの分子構造や分子動力学について何かを導くことはできない」とMITの物理学者アラン・アダムズは説明する。
「なぜなら、流体としての記述は、水について考えるためのもっとも基本的な方法ではないからだ。一方で、すべての分子がどこにあってどのように動いているかがわかれば、原理的には、水全体や水面の特徴に関するどんな事柄も導くことができる。つまり、ミクロな記述にはマクロな情報が含まれている」。
そのため私たちは、ミクロな記述の方が基本的であり、マクロな性質はそこから創発するものだと考える。
そのことは、幾何学とどう関係するのか?
一般相対論によって重力は時空の湾曲の影響であることがわかっているが、低エネルギー状態における、その重力はプランクスケールにおいて破綻する。
そのため大勢の物理学者が、現在の重力理論であるアインシュタインの理論は、実際の現象に対する低エネルギー近似でしかないと結論づけている。
見ることのできない分子的プロセスから湖の水面の波が創発するように、重力と、その幾何学としての記述もまた、正確にどんなものかわかっていないが存在するはずだと仮定している超ミクロな過程から創発するのだと、彼らは考えている。
重力や幾何学が、私たちの探している、プランクスケールにおける量子幾何や量子重力の記述から「創発」するというのは、そういう意味だ。
プランクスケールにおける従来の幾何学の破綻は、幾何学者が愛する分野の「行き止まり」ではない。
普通、何か新しいことがわかったら、そこに至るまでの古い事柄は捨てられるのでなく、解釈しなおされて拡張される。
いままでの数々の発見において幾何学が中心的役割を果たしていることを踏まえれば、幾何学はやがて捨て去られるのでなく、より大きくよりよい何かの一部だと考えるしかない。
そのため、何と呼ぶにせよ量子幾何学は、幾何学を「拡大したもの」でなければならない。
幾何学がすでに成し遂げている偉大な事柄をすべて再現でき、さらに超微小スケールでの信頼できる物理的記述を提供してくれるものが必要だからだ。
現在「古典幾何学」と呼ばれているものは、わずか一世紀前にこれが幾何学だと考えられていたものよりずっと幅広い。
プランクスケールにおける現象には、ほぼ間違いなく、幾何学の新たな一般化や概念の拡張が関係してくるだろう。
ガウスの自然幾何学はリーマン幾何学の土台を敷き、さらにそのリーマン幾何学が、時空に関するアインシュタインの見事な洞察をもたらした。
ニュートンの重力理論はきわめて実用的であり、系の中の物体に作用する重力を計算するための単純な方法を提供してくれる。
とくに、問題の物体があまり高速では運動しておらず、重力ポテンシャルがあまり大きくない限りは、うまく機能する。
そこにアインシュタインが登場し、彼の新たな理論では、重力は物体間を伝わる力でなく時空の湾曲の結果であると理解された。
そうして私たちは、ニュートンの重力理論はそのより幅広い描像の特別なケースにすぎず、物体がゆっくり運動していて重力が弱いという極限でしか有効でないことを知った。
こうしてみると一般相対論は、その名前が示しているとおり、真に一般的だったことがわかる。
アインシュタインの特殊相対論を一般化した - 重力をもたない理論を拡張して重力を含むようにした - だけでなく、ニュートンの重力理論を一般化したものでもあったのだ。
物理学と同様に、幾何学に関しても、まったく同じ重大局面に近づきつつある。
古典リーマン幾何学は、量子レベルの物理を記述できないのだ。
そこで代わりに、新しい幾何学、すなわち、ルービックキューブに対してもブランク長さのひもに対しても同じく通用する、もっと一般的な記述を探すことになる。
問題はそれをどうやって進めるかだ。
アイザック・ニュートンが重力理論をつくろうとしていたときもそうだっただろうが、私たちも多かれ少なかれ暗中模索の状態にある。
ニュートンはその目標を達成するために新たな手法を考え出し、そこから微積分が生まれた。
ニュートンの数学が物理学に促されたように、今日の私たちの数学もそうであるべきだ。
物理学から何らかのインプットがなければ、量子幾何学をつくり出すことはできない。
幾何学の何らかの新解釈はいつでも思いつけるが、本当に実り多いものであるためには、幾何学は何か基本的なレベルで自然を記述していなければならない。
そして、ガウスが賢明にも言ったように、そのためには外部からの何らかの導きが必要だ。
現実に即した物理学は、数学が満たすべき技術的要求を与えてくれる。
古典幾何学を使うと、プランクスケールにおける物理には、離散的な変化や突然の不連続性が関係しているように見える。
そこで私たちは、量子幾何学がそうした不連続性を取り除いて、より単純に理解でき簡単に取り扱えるもっと滑らかな描像を生み出してくれることを期待する。
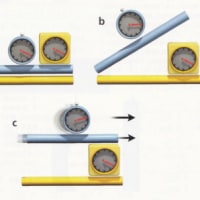
図1 物理学者ジョン・ホイーラーによる「量子泡」の概念。一番上の板は完全に滑らかに見える。しかしその表面を1000倍拡大すると(中央の板),不規則性が見えてくる。さらに1000倍拡大すると,小さなこぶがすべて大きな山となり,表面は滑らかとはほど遠くなる。
ひも理論は、ほぼ定義上、その種の問題を扱うものとされている。
ブライアン・グリーンは次のように説明する。
「ひも理論の基本構成部品は点でなく一次元のループなので、ひもの物理を記述するのに古典幾何学は正しい言語でないかもしれないと考えるのは、自然なことだ。しかし、幾何学のパワーは失われない。ひも理論は古典力学を修正した形式によって記述されるようで、ひものスケール - ブランクスケールより二、三桁大きいまたは小さいと考えられている長さスケール - に比べて系の典型的サイズが大きくなれば、その修正要素は姿を消す」。
最新の画像[もっと見る]
-
 タイムトラベルとタイムマシン?
9年前
タイムトラベルとタイムマシン?
9年前
-
 パウリの夢の数式に「虚数」が生み出された!
10年前
パウリの夢の数式に「虚数」が生み出された!
10年前
-
 「微細構造定数」137とパウリ&ユング
10年前
「微細構造定数」137とパウリ&ユング
10年前
-
 宇宙インフレーション 超弦理論
10年前
宇宙インフレーション 超弦理論
10年前
-
 拡張標準モデルとは?
10年前
拡張標準モデルとは?
10年前
-
 拡張標準モデルとは?
10年前
拡張標準モデルとは?
10年前
-
 相対性理論とローレンツ対称性
10年前
相対性理論とローレンツ対称性
10年前
-
 宇宙の起源に新説か?
10年前
宇宙の起源に新説か?
10年前
-
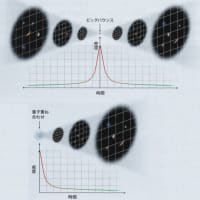
 宇宙の始まりは「ビッグバウンス」?
10年前
宇宙の始まりは「ビッグバウンス」?
10年前
-
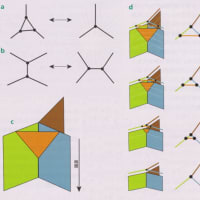 「スピンの泡」が時空に対応する、ループ量子重力
10年前
「スピンの泡」が時空に対応する、ループ量子重力
10年前










※コメント投稿者のブログIDはブログ作成者のみに通知されます