前回は、物質について述べましたが、我々が一般的に示している3次元とはどういうものなのでしょうか。
物質が存在するためには、空間3次元と時間という(3+1)次元の時空間を設定しなければなりません。そしてこの時空間は3次元座標(x、y、z)に時間(t)という1次元を加えることを大前提として物理学が発展してきました。
この感覚は、今までの古典力学と数学という組み合わせの中で次元を設定しようとした場合に、最も物理学者・数学者の両方を納得させるものだったのです。
しかし、前回にフラクタル次元の話をしましたが、このフラクタル次元という立場から考察すると、空間次元の3次元については納得できますが、時間に関しては不満が残ってしまいます。
なぜなら、原子核や電子を考慮した現代物理学の立場で「物質」を観察した場合、この物質は原子核の中の陽子・中性子の運動、そして電子の運動が中心になります。
この原子の構成は地球上の物質、すなはち個体・液体・気体の3つの状態の全てに関係し、しかも個体の状態にあっても原子核や電子は運動しているのです。
この運動することに当然のごとく回転(スピン)という時間を伴った動きが現れます。そして、このスピンに関わってくる素粒子がニュートリノなのです。
また、素粒子のスピンに関しては右巻(+)と左巻(-)の2通りあることが知られていますので、この2通りを時間次元とすると(+・-)の2次元として捉えても良いのではないでしょうか。
そうしますと、物理的な時空間は物質3次元プラス時間2次元の5次元まで拡張することが可能です(ここでは実数次元について述べているのですが、虚数次元の時にもスピンが絡んできますので+・-の2次元としておきます)。
さて、ここまで述べてきた次元構造ではフラクタル次元などは存在しなくても良いように思われます。しかし、現代物理では物質の状態にプラズマ状態という第4の状態が加わってきています。
この状態が地球の磁気圏とも関係して、非常に複雑な状態をこの地球上に及ぼしています。この磁場には必然的に電場を伴われています。そして、この電磁場には「光」と「波動」はこれまた切っても切れない関係があります。
20世紀になってアインシュタインの提唱した、「光速不変の法則」が現代物理学では常識のようになっております。しかし、この「光」と「波動」において、片方の「光」だけを不変にしてしまったために「波動」だけが変化しなくてはいけない状況が生まれてしまいました。
はたして、このようなことが在っても良いのでしょうか?
さて、これからフラクタル次元の話に入っていくわけですが、このフラクタル次元を導入するにあたって、どうしても必要なことが二つあります。一つ目は、プラズマ状態という物質の第4の状態です。
そして二つ目が、先ほどの「光」と「波動」なのですが、この「光と波動」を同等の二つの状態として考えると次元構造にどのような変化が生じてくるか、ということです。
以上の二つの条件には、どちらとも電磁場が関係してきます。この電磁場を見直すことで、今までの物理学的概念を根本から書き改めていく必要性が、このフラクタル次元に潜んでいます。
今回はここまでとします。
前回は、この言葉で終了しています
「タイムトラベルは、物理学の基本法則に反するのだろうか?」
一九九二年、スティーヴン・ホーキングは、このタイムトラベルの問題に最終解答を与えようとしました。直感的に、彼はタイムトラベルの可能性を否定し、時間を行き来する旅が休日のピクニックぐらい簡単にできるのなら、未来から来た観光客がわれわれを眺めて写真でも撮っているはずだと考えたのです。
しかし、物理学者はよく、T・H・ホワイトの大河小説『永遠の王』の一節を引縫合いに出します。アリの共同体が「禁じられていないものはすべて強制である」と表明しているくだりです。
要するに、タイムトラベルを禁じる物理学の基本法則がないのなら、タイムトラベルは必ず物理的に可能だというわけです。
これに対しホーキングは、「宇宙検閲仮説」なるものを提唱しました。タイムトラベルを妨げ、それゆえ「歴史を歴史家の安心できるものにする」仮説です。これによれば、タイムトラベルはある種の物理学的原理に反するので不可能ということになります。
このホーキングの「宇宙検閲仮説」の問題は、ブラックホールや裸の特異点が顔を出す時には必ず話題に上ります。前々回にも書きましたように、ホーキングが負けを認めたのですが、今回は、真空に出入りする微小な泡、すなはち、微小なワームホールやベビーユニバースについて、宇宙検閲仮説を検証してみます。
ワームホールの解はひどく扱いにくいため、ホーキングは単純化した宇宙の分析から議論を始めました。その宇宙はメリーランド大学のチャールズ・ミスナーが見つけたもので、タイムトラベルに必要な要素がすべて含まれていました。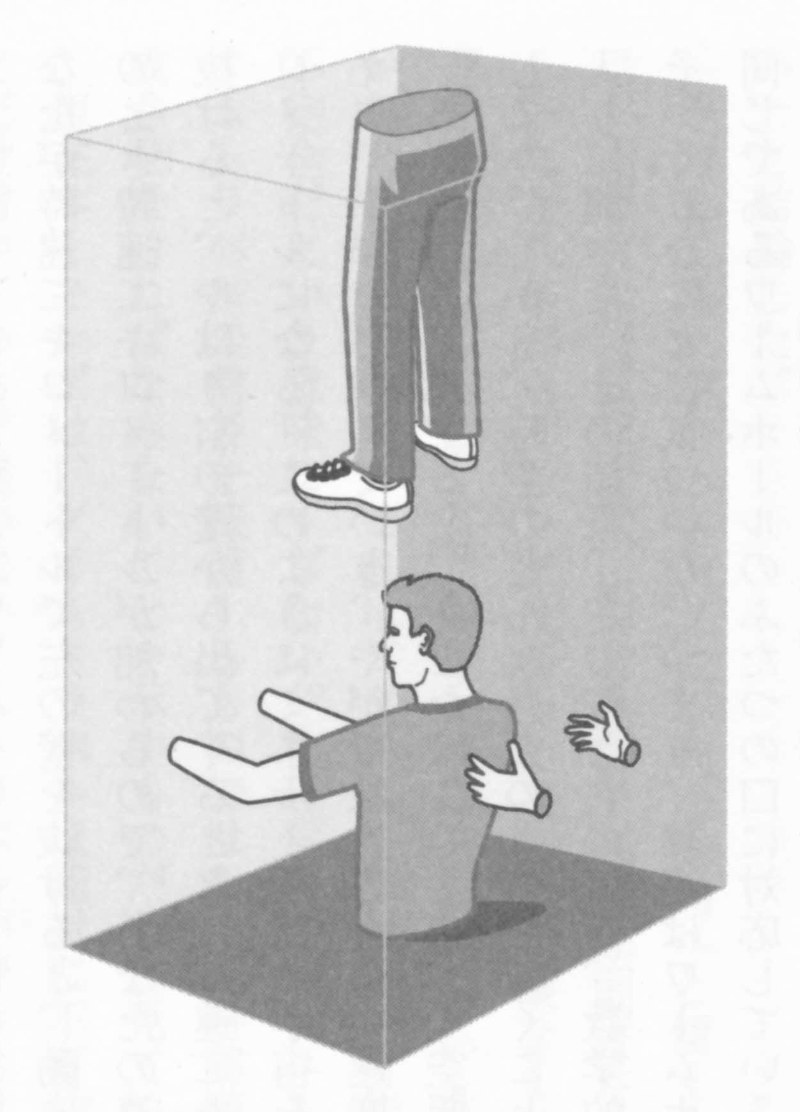
図:ミスナー空間
ミスナー空間では、たとえば寝室が全宇宙になる。向かい合う壁がすべて同一になり、一方の壁に入るとそのまま反対の壁から出てくるのだ。同様に天井も床と同一である。ミスナー空間は、ワームホールと同じ空間的構造をもちながら数学的にはるかに扱いやすいので、よく研究対象となる。壁が動けば、ミスナー空間でタイムトラベルも可能になる。
この「ミスナー空間」は理想化された空間で、そこではたとえば寝室が全宇宙になるのです。寝室の左側にある壁の各点が、右側にある壁の相対する点と同一だとしてみましょう。すると、左側の壁に歩いて行っても、ぶつかって鼻血を出す羽目にはならず、壁をすり抜けて右側の壁からまた寝室に出てこられるのです。左側の壁と右側の壁は、ある意味で円筒の面のようにつながっているのです。
さらに、前の壁の点が後ろの壁の点と同一で、天井の点と床の点も同一としてみましょう。そうなると、あなたはどの方向へ歩いても壁をすり抜けて寝室へ戻ってきてしまいます。つまり部屋から抜け出せなくなり、まさに寝室が全宇宙になるのです。
そしてまたなんとも奇妙なことに、左の壁をよく見ると、実は透明になっていて、そっくり同じ寝室が見えるのです。しかも、その寝室にはあなたのそっくりさんもおり、ただしこちらに背中を向けていて前は見えません。上や下を見ても、やはりあなたのそっくりさんが見えるのです。それどころか、前後にも上下にも無限にあなた自身の姿が続いているのです。
ただし、あなた自身との対面はとうていできません。振り返ってそっくりさんたちの顔を見ようとしても、彼らも振り返るので顔を合わせられないのです。しかし、寝室がかなり狭ければ、壁に手を突っ込んで目の前のそっくりさんの肩をつかむことができます。すると、あなたは背後のそっくりさんにも肩をつかまれてぎょっとするでしょう。また、左右の手を伸ばして両隣のそっくりさんの手をつかむこともでき、このとき無限に続いているあなたが手を握り合うことになるのです。結局のところあなたは、宇宙をぐるりと一周して自分と手をつないでいるのです。
ミスナー空間で、周囲の壁があなたに迫ってくる場合を考えてみると、実に面白いことになります。たとえば寝室がつぶれていき、右の壁が時速2キロメートルであなたに近づいてくるとします。あなたが時速2キロメートルで左の壁を抜けると、動いている右の壁から戻ってくることになりますが、このとき時速2キロメートルが加わるので、あなたの速度は時速4キロメートルになるのです。ふたたび壁を抜けると、やはり右の壁から出てくるときに時速2キロメートルが加わり、あなたの速度は時速6キロメートルになる。このようにミスナー空間の宇宙を何巡もすると、あなたの速度は時速6キロ、8キロ、10キロと増えていき、やがては途方もない速度になって光速に近づくのです。
ある臨界点に達すると、あなたはこのミスナー空間をあまりに速く動きすぎて、時間を逆戻りしてしまいます。しかも、時空のどんな過去の点へも行くことができるのです。ホーキングはこのミスナー空間を念入りに調べました。その結果、左の壁と右の壁が、数学的に見て、ワームホールのふたつの口とほとんどそっくりなことに気づいたのです。つまり、寝室はワームホールと似ていて、左の壁と右の壁は、そっくり同じであるワームホールのふたつの口に対応しているのです。
それからホーキングは、このミスナー空間が古典論的にも量子力学的にも不安定であると指摘しました。たとえば左の壁を懐中電灯で照らすと、光は右の壁から出てくるたびにエネルギーを増していきます。こうして動く壁による青方偏移を起こしながらエネルギーを増す光は、ついには無限大のエネルギーに到達することになりますが、それはありえません。ありえるとすると、途方もないエネルギーに達した光がそれ自身の莫大な重力場を生み出し、寝室を--ひいてはワームホールを--押しつぶしてしまうからです。
したがって、ワームホールは、あなたが入ろうとするとつぶれることになります。また、空間に含まれるエネルギーや物質の量を示す、エネルギー運動量テンソルというものも、放射が二枚の壁を無限回通り抜けるので、無限大になります。
ホーキングには、これがとどめの一撃となるように思えました。量子論的な放射の影響が次第に増して無限大に発散し、タイムトラベラーを死なせ、ワームホールが閉じてしまうだろうと。
ホーキングがそれを論文に記して以後、彼の提起した発散の問題は物理学界で盛んに議論され、宇宙検閲仮説について賛否両論を呼んだのです。何人かの物理学者は、大きさや長さなどを変えて適切なワームホールを選ぶことで、ホーキングの証明に抜け穴を見つけはじめました。
エネルギー運動量テンソルが、一部のワームホールの解では確かに発散するが、ほかの解では明確な値をもつことを明らかにしたのです。
ロシアの物理学者セルゲイ・クラスニコフは、さまざまなタイプのワームホールに対してこの発散の問題を検討し、「タイムマシンが不安定でなければならないことを示す証拠は微塵もない」と結論しました。
そのまま流れがホーキングに不利な方向へと傾くなか、プリンストン大学の物理学者リー・リシンは、「閉じた時間的曲線の出現を妨げる物理法則はない」という反宇宙検閲仮説まで打ち出した。
一九九八年、ホーキングは多少の退却を余儀なくされたのです。その際にこう書いています。「エネルギー運動量テンソルが(ある種のケースでは)発散しないという事実は、逆反応が宇宙検閲を強制しないことを示している」これは、タイムトラベルが可能だというわけではなく、われわれの理解がまだ不完全だという意味にすぎません。
物理学者のマシュー・ヴィサーは、ホーキングの仮説の失敗を、「タイムトラベルの信者を擁護するものではなく、宇宙検閲の問題を解決するには量子重力理論を完成させなければならないことを示すものだ」と見ています。
現在ホーキングは、タイムトラベルは絶対に不可能だとは言わず、ただ非常に実現の可能性が低いとだけ言っています。確かにタイムトラベルができる見込みはきわめて薄いようです。だが、その見込みを完全には排除できません。
正と負のエネルギーをなんとか大量に利用して安定性の問題を解決できたら、タイムトラベルは本当にできる可能性があるのです。
ー九九一年、プリンストン大学のJ・リチャード・ゴット三世が、アインシュタインの方程式に対し、タイムトラベルを可能にするもうひとつの解を提示しました。彼のアプローチは興味深いものです。というのも、回転する天体や、ワームホールや、負のエネルギーをかなぐり捨てて、まったく新しい角度から取り組みだしたからです。
ゴットは、宇宙論を研究していて、多くの理論で予言されているビッグバンの遺物「宇宙ひも」に関心を抱くようになりました。宇宙ひもの太さは原子核の直径にも満たないようですが、質量は恒星並みで、空間に何百万光年も伸びていると考えられています。
ゴットは、アインシュタインの方程式に、宇宙ひもの存在を許す解を初めて見出しました。だがそこで、その宇宙ひもについて奇妙な点に気づくのです。
宇宙ひもを互いに近づけると、衝突する直前、これを使ってタイムマシンができるのです。まず彼は、衝突しかけている宇宙ひもを迂回してぐるりと一周した場合、空間が縮まり、奇妙な性質が現れることを見出しました。
たとえばテーブルのまわりを一周するとして、そのあいだに回る角度は360度になります。しかし、互いにすれ違おうとしている二本の宇宙ひものまわりを宇宙船で一周すると、空間が縮んでいるので、回る角度は360度より少なくて済みます(これは円錐の空間的構造である。円錐面を一周する場合、面を展開してみるとやはり回る角度は360度より少ない)。
したがって、二本のひものまわりを高速でめぐれば、全体の距離が見かけより小さいため、なんと光速を超えられる可能性があるのです。それでいて、特殊相対性理論にも反しません。宇宙船を基準とする座標系では光速を超えていないからです。
ところでこれは、衝突しかけている宇宙ひものまわりをめぐると過去へ行けるということでもあります。
ゴッドはこう振り返っています。
「この解を見つけたとき、すっかり興奮した。解には、光速より遅い速度で運動する正の密度をもつ物質しか使っていなかった。これに対し、ワームホールの解には、エキゾチックな負のエネルギー密度をもつ物質(無より軽いもの)が必要なのだ」
とはいえ、タイムマシンにはとてつもないエネルギーが必要になります。
宇宙ひもは存在するとしてもまれで、衝突しかけている宇宙ひもとなるとさらに少ない、と指摘する批判もありました。
そこでゴットは次のように考えたのです。高度な文明は、宇宙空間に一本の宇宙ひもを見つける。彼らは、巨大な宇宙船と道具を使って、そのひもを少しひしゃげた四角形のループにする。そしてこのループがそれ自体の重力によってつぶれると、宇宙ひもの二辺が光速に近い速さですれ違う可能性があり、一時的にタイムマシンができるというわけである。
ただしゴットもこのように認めています。
「一周して一年さかのぼれるだけの大きさをしたつぶれるループは、銀河全体の半分以上におよぶ質量、すなはちエネルギーをもつことになる」
今回は、ワームホールを追求することで「タイムトラベル」の可能性を探ってきました。しかし、そこには「宇宙ひも」という不可思議なものが出現してしまいました。
前回で「タイムトラベル」シリーズはとりあえず終了したのですが、カー・ブラックホールが中心となり、閉じた時間の環(CTL)とペンローズ図が中心となってしまいました。このCTLに沿って進めば、やがて自分のいた過去の世界に行き着くことになるでしょう。
もし、そうなれば、原理的にタイムマシンをつくることは可能となるはずです。しかし、それにはCTL構造をもった通路としての四次元時空をつくりださなくてはなりません。
「タイムトラベル」シリーズでは、タイムトラベルの通路としてのブラックホールを中心として書いてきました。タイムトラベルですから、場所の設定は地球以外考えられません。しかし、この場所設定を地球外の天体として設定できないのでしょうか。
今回は、宇宙船に乗って、宇宙へと飛び出してみたいものです。
一九八五年、天文学者のカール・セーガンが、小説『コンタクト』を執筆中、ヒロインが恒星ヴェガまで旅行できる方法を具体的に考えようとしました。それには、ヴェガまで行くだけでなく、地球へ戻ってくる往復の旅ができなければならず、ブラックホールの作るワームホールでは帰ってこられないので不可能ではないのかという疑問を持ちました。した。
そこでセーガンは物理学者のキップ・ソーンに助言を求めています。これをきっかけにソーンは、アインシュタインの方程式に、それまでの多くの問題を回避してタイムマシンを使った「タイムトラベル」ができるような新しい解を見つけ、物理学界に衝撃を与えました。
一九八八年、同僚のマイケル・モリスとウルヴィ・ユルツェヴァーとともに、「エキゾチックな負の物質」や「負のエネルギー」といった不可解な物質やエネルギーをどうにかして入手できれば、タイムマシンが作れることを明らかにしたのです。
世の物理学者は当初、この新しい解に懐疑的な見方を示しました。エキゾチックな物質などだれも見たことがなかったし、負のエネルギーはほんのわずかな量しか存在しないからです。それでも、この解はタイムトラベルを考えるうえで突破口を切り開いたのです。
負の物質や負のエネルギーには大きな利点があります。それらのおかげでワームホールが通行可能になり、事象の地平線を気にせずに往復の旅ができるようになるのです。それどころか、ソーンらは、そうしたタイムマシン(タイムワープする宇宙船)での旅行が、旅客機に乗っていて感じるストレスと比べてもずっと快適かもしれないことに気づきました。
しかし、問題がひとつあります。それは、エキゾチックな物質(つまり負の物質)が非常に奇妙な性質をもっているのことです。反物質は存在が知られ、地球の重力場で地面に向かって落下するはずですが、これと違い、負の物質は上へ向かうのです。
反重力をもつため、地球の重力を受けると浮上するのです。負の物質は、通常の物質にも、ほかの負の物質にも、引きつけられはせず斥けられます。したがって、たとえ存在したとしても、自然界で見つけるのはきわめて難しいのです。
四十五億年前に地球ができたとき、地球上の負の物質はすべて深宇宙へ飛んでいってしまったでしょう。だから負の物質は、どんな星からも遠く離れた宇宙空間になら浮かんでいるかもしれません(負の物質は通常の物質と反発するので、通りかかる恒星や惑星にぶつかることはないでしょう)。
負の物質は見つかっていません(そして存在しない可能性も高い)が、負のエネルギーは、きわめてまれではあっても物理的に存在できます。
一九四八年、オランダの物理学者ヘンドリック・カシミールは、二枚の帯電していない金属板を平行に置くと負のエネルギーが生まれる可能性があることを示しました。
ふつうに考えれば、二枚の板は帯電していないのだから静止したままのはずです。ところがカシミールは、この帯電していない平行な板のあいだに非常に小さな引力が働くことを明らかにしました(カシミール効果)。
一九五八年、この微弱な力が実際に測定され、負のエネルギーの実在が確かめられました。このカシミール効果は、真空がもつ奇想天外な性質によるものです。
量子論によれば、空っぽの空間には、無から生まれたり消えたりする「仮想粒子」に満ちています。これはエネルギー保存則に反しますが、ハイゼンベルクの不確定性原理により、非常に短い時間ならば、古典論の法則を破ることも許されるので可能です。
たとえば電子と反電子(すなわち陽電子)が、不確定性原理により、無から生まれて出会い、対消滅するという確率はわずかながらあるのです。しかし平行な板のすきまは非常に狭いため、仮想粒子はそのすきまに生じにくい、つまり、板のすきまより周囲のほうが仮想粒子は多くなるので、結果的に平行な板を両側からわずかに押す内向きの力が生じるのです。
この効果は、一九九六年、ロスアラモス国立研究所のスティーヴン・ラモローが厳密に測定しました。測定で確かめられた引力は非常に小さく、アリの三万分の一の重さに相当する程度だったのです。しかし板のすきまを狭めれば、引力は大きくなります。
いよいよ、ソーンがイメージした宇宙船の仕組みを示す時が来ました。高度な文明はまず、二枚の板をきわめて小さな間隔で平行に配置します。次にこの平行な板を球に変形すると、二重の殻をもつ球ができます。そうした球を二つ作り、そのあいだにどうにかしてワームホールを張りわたせば、ふたつの球が空間的なトンネルでつながります。このときそれぞれの球はワームホールの口を覆っていることになります。
通常、ふたつの球で時間は同期して流れます。ところが、片方の球を宇宙船に乗せて亜光速で飛ばすと、宇宙船では時間の流れが遅くなるので、ふたつの球の時間はもはや同期しなくなります。宇宙船の時計は、地球の時計よりも遅く時を刻むのです。そこで地球側の球に飛び込むと、ふたつの球をつなぐワームホールに吸い込まれ、宇宙船側の球から出ることができる。出た先の宇宙船は、地球より過去の時間なのです(ただし、このタイムマシンでは、マシン自体を作ったときより過去へは行けません)。
ソーンの解は、発表されると一大センセーションを巻き起こしましたが、実際にそのタイムマシンを作るには、高度な文明にとっても大きな障害があります。まず、きわめて希少な負のエネルギーを、大量に手に入れる必要があるのです。
この種のワームホールでは、口を開けておくのにぼう大な負のエネルギーが必要です。カシミール効果で負のエネルギーを作るとしても、その効果は非常に小さいので、原子よりずっと小さなサイズのワームホールしかできず、ワームホールを通る旅は現実的でなくなります。カシミール効果以外にも、負のエネルギーを生み出す手だてはあるのでしょうが、どれも実現は非常に難しいのです。
たとえば物理学者のポール・デイヴィスとスティーヴン・フリングは、高速で鏡を動かすと負のエネルギーが生じることを明らかにしました。動く鏡の前面に負のエネルギーがたまっていくのです。だが、負のエネルギーを得るには、鏡を光速に近いスピードで動かす必要があり、しかも、カシミール効果と同様、生じる負のエネルギーはわずかです。
負のエネルギーを引き出す方法には、高出力のレーザー光線を利用するものもあります。レーザーのエネルギー状態には、正のエネルギーと負のエネルギーが共存する「スクイズド状態」があるのですが、この効果を利用する手段も実現は至難の業なのです。
一般に負のエネルギーのパルスは10の-15乗秒間しか持続せず、そのあとに正のエネルギーのパルスが続きます。そんななかで正のエネルギー状態と負のエネルギー状態を分離するのは、不可能ではないがきわめて難しいことです。
最後に、ブラックホールも、事象の地平線の近くで負のエネルギーを生み出すことがわかっています。ジェイコブ・ペッケッスタインとスティーヴン・ホーキングが示したように、ブラックホールは、少しずつエネルギーを「蒸発」させているので完全にブラック(黒)ではありません。
不確定性原理によって、ブラックホールの途方もない重力から放射が漏れ出るトンネル効果が生じているのです。
その一方で、ブラックホールは蒸発によりエネルギーを失うため、事象の地平線は次第に縮小するのです。一般に、ブラックホールに正の物質(恒星など)が放り込まれると、事象の地平線が広がり、反対に、負の物質が放り込まれるとすれば、事象の地平線は縮小することになります。
したがって、ブラックホールの蒸発は、実質的に事象の地平線の近くに負のエネルギーを生み出す現象なのです。
ホーキングは、一般に負のエネルギーが、あらゆるワームホールを安定させるのに必要なことを明らかにしました。理屈は簡単です。正のエネルギーは、物質やエネルギーを集約するようなワームホールの開口部を作ります。
だから光はワームホールに入るときに収斂します。ところが、この光がワームホールの向こう側から出るときには、ワームホールのなかのどこかで広がってもとに戻らなければなりません。
それを可能にしてくれるのは、負のエネルギーの存在だけなのです。さらに、負のエネルギーは反発力となるので、重力によるワームホールの崩壊を防ぐのにも欠かせません。
したがって、タイムマシンすなわちワームホールを作るには、ワームホールの口を開けて安定させておけるだけの負のエネルギーを見つける必要がありそうです(大きな重力場があれば負のエネルギー場もたくさんできることは、多くの物理学者が明らかにしている。そのため、いつかは重力による負のエネルギーがタイムマシンの動力に利用できるようになるかもしれない)。
このようなタイムマシンには、もうひとつ障害があります。
「ワームホールをどこで見つけるのか?」
という問題です。ソーンは、ワームホールが時空の泡というもののなかで自然に生じるという見方を利用しました。
この見方のおおもとは、古代ギリシヤの哲学者ゼノンが二千年以上も前に発した疑問までさかのぼります。移動可能な最小の距離はいくらかという疑問です。
ゼノンは、どんな川も渡れないことを数学的に証明してみせました。まず彼は、川幅が無限個の点に分けられることに気づいたのです。ところが、無限個の点を通過するには無限の時間がかかるので、川を渡ることはできなくなってしまいます。いや、さらに言えば、そもそも最初に動くことさえできないはずだったのです(それから二千年経ち、微積分が登場してようやくこの問題が解決された。微積分により、無限個の点を有限の時間で通過できることが示され、運動そのものが数学上可能となったのである)。
プリンストン大学のジョン・ホイーラーは、アインシュタインの方程式を調べて「最小の距離」を割り出しました。プランク長さ(10の-33乗センチメートル)のオーダーにあたる極微の距離では、アインシュタインの方程式で求めた空間の曲率が非常に大きくなることを見出したのです。言い換えれば、プランク長さでは、空間は平坦でなく大きく湾曲している--よじれて「泡立って」いる--ことになるのです。
空間はでこぼこで、真空に出入りする微小な泡で満ちているのです。空っぽの空間であっても、極微の距離では時空の微小な泡でたえず沸き立っており、それらの泡は実のところ微小なワームホールやベビーユニバースに相当するのです。
通常、「仮想粒子」は電子と反電子のペアであり、それらが一瞬現れてはぶつかって対消滅します。ところがプランク長さでは、微小な泡は丸ごとひとつの宇宙やワームホールで、それがひょっこり現れては真空に消えていく。
ひょっとしたらわれわれの宇宙も、時空の泡になって浮かぶそうした小さな泡のひとつとして生まれ、なぜかはわからないが突然インフレーションを起こしたのかもしれません。
このようにワームホールは泡として自然に見つかるので、ソーンは、高度な文明ならどうにかしてその泡からワームホールを取り出し、負のエネルギーで広げて安定させられるのではないかと考えました。これはきわめて困難なプロセスに違いないだろうが、物理法則を逸脱してはいません。
ソーンのタイムマシンは、工学的に見れば作るのが非常に難しいにしても、理論的にはありそうに見えます。しかしここで、三つめの厄介な問題があるのです。
「タイムトラベルは、物理学の基本法則に反するのだろうか?」
という問題です。
今回で、「タイムトラベル」シリーズは終了します。かなり難しい内容になっていますが、今後は別のシリーズ、「タイムトラベラー・タイター」でもっと解りやすく書いていきたいと思っています。今回は、「タイター」シリーズでの図表を掲載しています。
前回は、宇宙の特異点の記述で終了しています。裸の特異点が存在すると、理論的に因果関係を予測することができなくなります。ロジャー・ペンローズは、自然界にはそんなものは存在しないだろうと考え、「宇宙検閲仮説」というものを提唱しました。
そして、この「特異点」と「宇宙検閲仮説」については、ここのブログに詳しく書いていますので、以下の記事を参考にされてください。
「特異点で何が起きているのか?」1~3
ここで、前回までに書いてきた、ブラックホールの種類をまとめてみます。
ブラックホールの性質を決めるものは,質量、回転、電荷の3つしか在りません。そして、自転しているブラックホールは角運動量を持つことが知られています。ブラックホールは自転・電荷の有無によって4種類の基本タイプに分けられます。そして、最終的にはどんなブラックホールもカー=ニューマン・ブラックホールになると言われているのです(下図1参照)。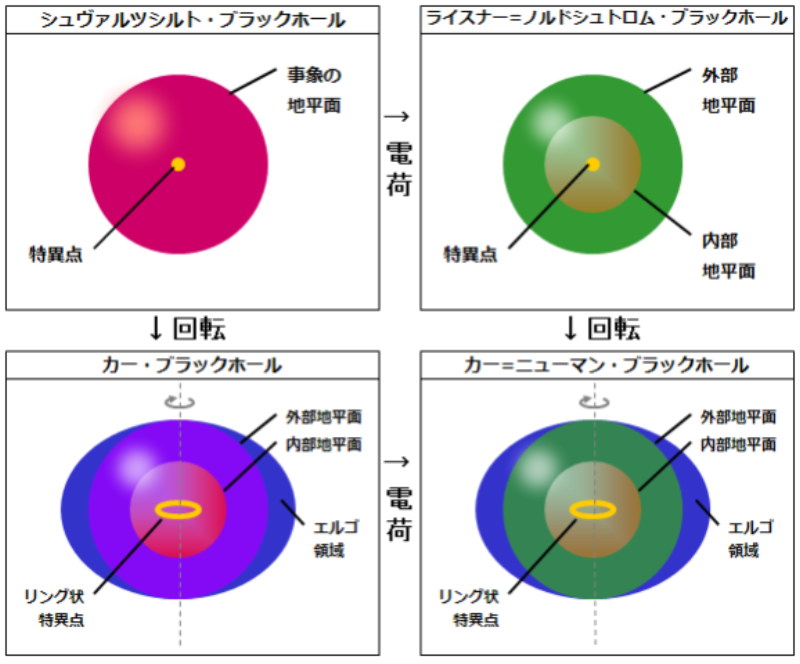
図1:ブラックホールの4種類
シュヴァルツシルト・ブラックホール:回転なし、電荷なし、点状特異点
ライスナー=ノルドシュトロム・ブラックホール:回転なし、電荷あり、点状特異点
カー・ブラックホール:回転あり、電荷なし、リング状特異点
カー=ニューマン・ブラックホール:回転あり、電荷あり、リング状特異点
さて今回は、超極限のカー物体のペンローズ・ダイアグラムを下図2に示します。超極限状態になると、カー・ブラックホールで存在していたペーパードール・トポロジーは消え失せ、一対の正の時空間と負の時空間のみになり、リング状特異点により隔てられています。
リング状特異点が露出することにより、時空全体がCTL領域となっています。われわれの宇宙に超極限のカー物体が一個存在するだけで、時空全体が影響を受けます。つまり、いたるところに過去への入口が存在するかもしれないのです。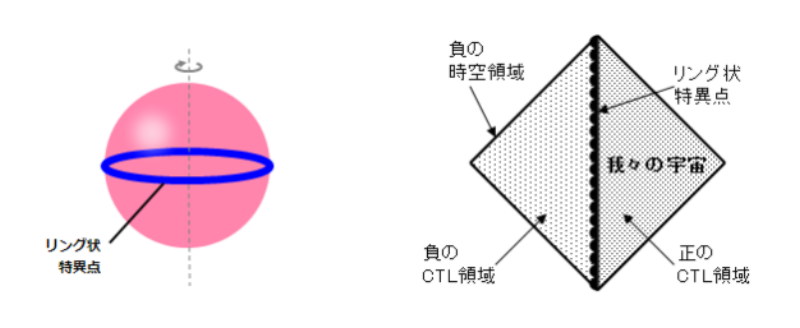
図2:超極限のカー物体(SEKO=super-extra Kerr object)とペンローズ・ダイアグラム
裸の特異点が存在すると、物理現象の因果関係が破綻するため、宇宙検閲仮説というものが考え出されました。裸の特異点が存在しないように、宇宙自体が検閲し、禁止しているという仮説です。
1992年にシャピーロとトイコルスキーによって示された、円盤状の塵の崩壊のシミュレーションでは、崩壊した軸上の少し外れた点において、曲率が無限大になり宇宙検閲仮説は破綻しました。
このシミュレーションでは事象の地平面ができなかったので、裸の特異点が形成されたと考えられました。この結果は、宇宙検閲仮説が破れていると受け取られています。
ホーキングは、キップ・ソーンと、「宇宙検閲仮説」は守られるかどうかで賭けをしていましが、このシミュレーション結果に対し、数年後、ホーキングが負けを認めました。したがって、裸の特異点が存在する可能性は高くなったといえます。
超極限のカー物体(SEKO)は裸のリング状特異点を持つ一個の反重力宇宙で、もし我々の宇宙にSEKOが一つでもあれば、時空全体がCTLとなり、全ての場所が過去への旅への出発点となるのです。
SEKOのもっとも興味深い特徴は、その特異点の周りを適切な方向に回れば時間を逆行することが出來ます。その上、そういう周回航行をすればブラックホールの膜の内側ばかりでなく、時空の全領域への到達が可能になります。
原則的にはSEKOに近づきその周りを二、三周すれば、特異点をくぐり抜けたりしてよく分からない新しい宇宙へ飛び込む必要はなく、過去のどこにでも行けるタイムトラベルが可能となります。
このように、カー・ブラックホールが超極限状態になると、特異点がむき出しの状態になり、タイムトラベルが可能であることを示しました。では、その超極限のカー物体が、この宇宙に存在するのでしょうか。
観測結果によると、各銀河の中心には、巨大なブラックホールが存在するらしいことが分かってきました。しかし、タイムトラベルするために、そのブラックホールの近くまで行くのは大変なことです。
もし、ミニブラックホールを人工的に作ることができれば、タイムマシンを実現することが出来るのです。
しかし、現実世界でのタイムトラベルを可能にするためには、SEKOにとっては欠かすことの出来ない特徴の一つとしての時間的特異点に難点が生じます。それは、量子効果によって時間的特異点が空間的特異点へと変換されてしまいます。そのため、時空の特徴が安定してしまい、タイムマシンに利用できないかもしれないのです。
また、通常のブラックホールを回転させてSEKOを作る事は不可能かもしれません。それは、ブラックホールを「質量<角運動量」にする必要があるのですが、角運動量が増大するにしたがって回転を上げる軌道が減少します。その結果、ゼロに近づくか、または回転体の反発によりSEKO自体を維持することが不可能になるのかもしれません。
現在、特異点が二つあるブラックホールの解については、まだ誰も解いてはいません。
しかし、この二つのブラックホールを利用したタイムマシーンに乗ってタイムトラベルをしてきたという、ジョン・タイターの話も聞いてみる必要がありそうです。
そのタイムマシンの原理図です(下図表参照)。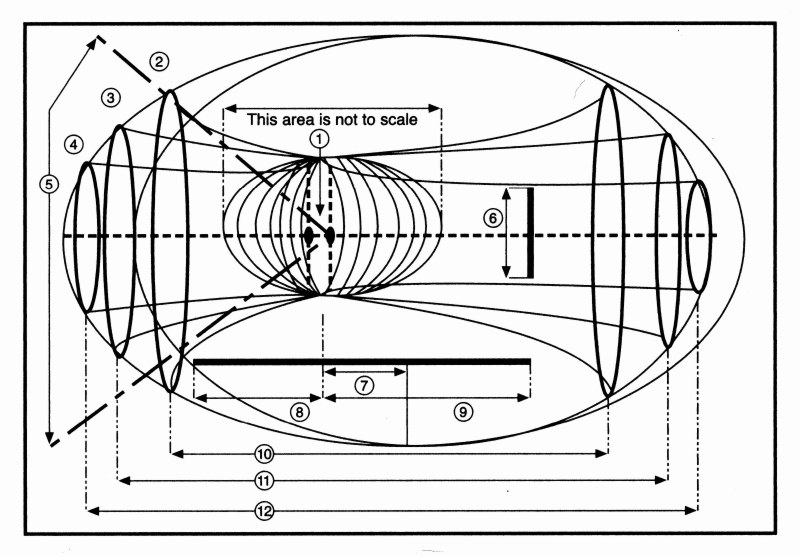
①カー領域の双対特異点 ⑦質量オフセット
②負時間領域の出力 ⑧後方質量分布
③無時間領域の出力 ⑨前方質量分布
④正時間領域の出力 ⑩負時間事象の地平線
⑤X軸出口円錐 ⑪無時間事象の地平線
⑥垂直安全距離 ⑫正時間事象の地平線
この図表は、「超極限のカー物体(SEKO)」に似ています。SEKOは、質量による重力よりも自転による角運動量の方が大きく、特異点が裸の状態になった物体です。しかし、SEKOは、特異点が一つだけなのですが、上の図では特異点が二つあります。
この図では、事象の地平線は存在しているのですがドーナツ状になっており、上下方向からは特異点がむき出しになっています。特異点が二つあるためか、質量の重心が中心からずれています。
インターネット上で、ジョン・タイターは、次のように言っています。
『タイムトラベルは、重力の強さを自在に変化させることにより達成される。人工の双対ミクロ特異点を取り巻く質量と重力場に電子を注入して荷電させ、「カー局所場」ないし「ティプラー重力シヌソイド」内の事象の地平線の直径を拡大する。ドーナツ状特異点の環内に物質を通過させ、別の世界線へと送り込む動作をシミュレート操作して、局所場を適合・回転・移動できれば、安全なタイムトラベルが可能となる。』
回転するブラックホールに電荷を注入すると、「カー=ニューマン・ブラックホール」になります。カー=ニューマン・ブラックホールは、特異点の周囲に正のCTL領域が生成されるので、リング状特異点を通り抜けなくてもタイムトラベルが可能となります。
電荷を注入することにより、重力に打ち勝つ反発力が生じるため、ドーナツ状特異点の直径が拡大します。さらに、特異点の自転による角運動量によってもドーナツ状特異点の直径が拡大するため、特異点が裸の状態になると考えられます。
このようにして、特異点が裸の状態になり、正のCTL領域がタイムマシン全体を包み込むことにより、タイムトラベルが行われると考えられます。
今回は、いよいよ、カーのブラックホールについてです。
シュワルツシルトとライスナー=ノルドストロームの解が発表されてから約半世紀が過ぎた1963年に、ニュージーランド生まれの物理学者ロイ・カーが、強力な重力を持ち、高速で回転する物体のアインシュタイン方程式の解を発見しました。カー・ブラックホールのペンローズ・ダイアグラムを下の図1に示します。
このカー・ブラックホールには、三つの特徴があります。図1の左側を見ると解りますようにリング状の特異点、負の時空領域、負のCTL(Closed Time Link)領域、つまり負の閉じた時間の環の三つです。また、ライスナー=ノルドストロームのブラックホールと同様に、時間的特異点とペーパードール・トポロジーもあります。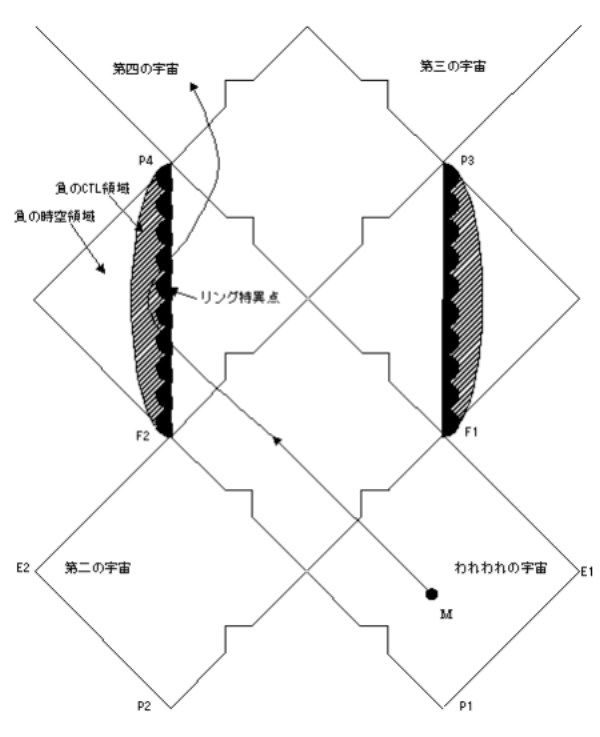
図1:カー・ブラックホールのペンローズ・ダイアグラム
まず最初は、リング状の特異点ですが、カー・ブラックホールには、特異点が点ではなく、回転軸を取り巻くリング状の形をしています。このため、無限に湾曲した領域を避けて、ブラックホールの中心に到達できるのですペンローズ・ダイアグラムでは、リング状特異点をギザギザの歯ではなく、丸い歯で表現しています。
次に、負の時空領域は、ブラックホールのリングの中心を通り抜けたところ、そこは元の宇宙ではなく、負の時空領域となっています。そこでは、G×r(Gは宇宙の重力定数、rは中心からの距離)が負になります。
中心からの距離が負になるというのは考えにくいので、重力が負になると考えられます。つまり、ブラックホールの中心に達するまでは、引っ張られる力を受けていたのですが、中心を通り抜けるとブラックホールから反発する力を受けるようになるということです。
そして.最後の三つめですが、リング状特異点の内側には、負のCTL領域、つまり負の閉じた時間の環が生じます。
リングの中心を通り抜けて、回転軸の周りを回転方向に回ると過去にさかのぼることができ、その回った回数によってどれだけ時間をさかのぼるかが決まります。そして、リングの中心を再び通って戻ると正の時空領域に戻ることはできますが、一方通行の膜があるので元の宇宙に戻ることはできず、別の宇宙へ抜けるはずです。
この別の宇宙とは、われわれの宇宙の離れた領域かもしれないし、パラレルワールドになっていて、われわれの宇宙とそっくりの別の宇宙かもしれないのです。
ロイ・カーが回転するブラックホールの解を発表してから2,3年後、ピッツバーグのエズラ・ニューマンとその同僚が、電荷を持ち回転するブラックホールの解を発表しました。今度は、カー=ニューマン・ブラックホールのペンローズ・ダイアグラムを下の図2に示します。
正のCTL領域が追加された形となっていることが解ります。この図2では、リング状特異点を通り抜けなくても、正のCTL領域に到達できるのです。この正のCTL領域により、負の時空領域を通過することなく、過去にさかのぼることができます。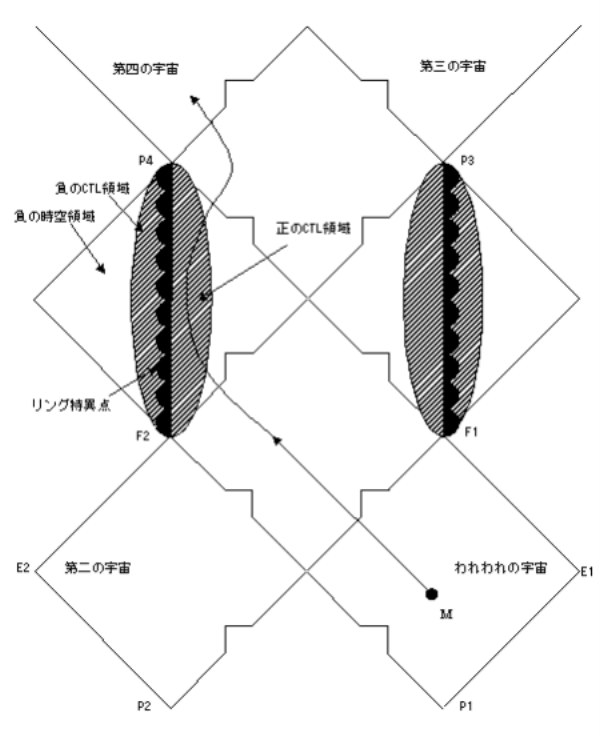
図2:ー=ニューマン・ブラックホールのペンローズ・ダイアグラム
上の図から解りますが、リング状特異点の内側には、正のCTL領域つまり正の閉じた時間の環が存在します。
カー・ブラックホールには正のCTL領域は存在せず、負のCTL領域しか存在しませんでした。しかも、負のCTL領域に行くにはリング状特異点の中心を通り抜ける必要があったのです。
下図3にカー=ニューマンのブラックホールのイメージ図を示します。リング状特異点に到達するまでに一方通行の膜が二つ存在しています。リング状特異点の内側領域に正のCTL領域が存在しています。リング状特異点の中心を通り抜けると負のCTL領域となり、さらに進むとそこは負の時空領域となっています(このイメージ図では想像しにくいので2図から類推してください)。正の時空領域に戻り、一方通行の膜を二つ抜けて出てくると、そこは別の宇宙となっています。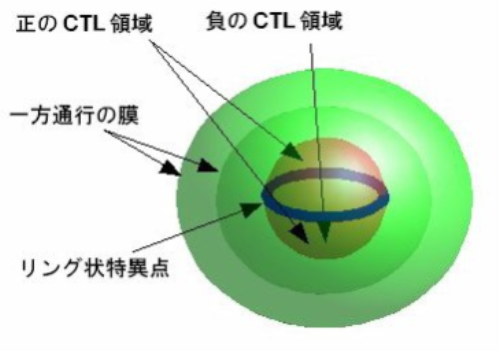
図3:カー=ニューマンのブラックホールのイメージ
カー=ニューマンのブラックホールは、リング状特異点の中心を通り抜けなくても正のCTL領域に到達できるので、そこで回転軸と反対方向に回転すると、その回った回数に応じて過去にさかのぼることができます。
ただし、一方通行の膜が存在するので、元の宇宙に戻ることはできず、別の宇宙へ行ってしまうようです。









