算額（その638）

算額（その638）

福島県郡山市田村町田母神地区 馬頭観世音（姉屋観世音）堂 明治11年
～落書き帳「○△□」～
３．四葉のクローバー
http://streetwasan.web.fc2.com/math15.5.10.html

等円 4 個とそれらの交点を通る円がある。緑色で示した部分の面積を求めよ。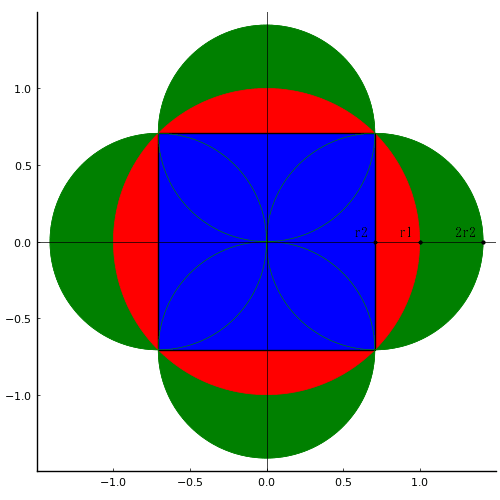
大円，等円の半径を r1，r2 とおき，図形の 1/8 （角度0度から45度まで）を考える。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r1, r2, b, r, g, x
r2 = r1/sqrt(Sym(2))
b = r2^2/2
r = PI*r1^2/8 - b
g = PI*r2^2/4 - r
println(g)

   r1^2/4

緑全部の面積はこれを 8 倍したもの，すなわち大円の面積の 2 倍である。

r1 = 1 として，上部の緑色の部分の面積は，積分により以下のようになる。これを4倍して大円の面積の2倍であることが確認できる。

eq = sqrt(r2^2 - x^2) + r2 - sqrt(r1^2 - x^2)
eq = eq(r1 => 1, r2 => 1/sqrt(Sym(2)))
integrate(eq, (x, -1/sqrt(Sym(2)), 1/sqrt(Sym(2)))).evalf() |> println

   0.500000000000000

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1
   r2 = r1/√2
   @printf("r1 = %g;  r2 = %g\n", r1, r2)
   plot()
   circlef(0, r2, r2, :green)
   circlef(0, -r2, r2, :green)
   circlef(r2, 0, r2, :green)
   circlef(-r2, 0, r2, :green)
   circlef(0, 0, r1)
   plot!([r2, r2, -r2, -r2, r2], [-r2, r2, r2, -r2, -r2], seriestype=:shape, fillcolor=:blue)
   circle42(0, r2, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(2r2, 0, "2r2 ", :black, :right, :bottom, delta=delta/2)
       point(r1, 0, "r1 ", :black, :right, :bottom, delta=delta/2)
       point(r2, 0, "r2 ", :black, :right, :bottom, delta=delta/2)
   end
end;

 

算額（その637）

算額（その637）

長野県上田市別所温泉 北向観音堂 文政11年(1828)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

2つの楕円が交差する中に等円が 4 個入っている。楕円の長径（差渡し）が 4 寸 9 分のとき，等円の直径が最大になるときの楕円の短径（差渡し）はいかほどか。

内接円の中心間の距離(eq1)，楕円と円が共通接点を持つ(eq2, eq3)，短径と円の中心の関係(eq4) があるが，eq1 〜 eq4 を一度に解くことができない。
それは，等円の半径は楕円の短径に依存するということが理由である。
そこで，例えば eq2, eq3, eq4 を連立させて r, x, y を求める。それぞれの式には b が含まれる。つまり，r, x, y は b により決定されるということである。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a::positive, b::positive, r::positive,
     x0::positive, x::positive, y::positive

a = 49//20
xx = sqrt((a^2 - b^2)*(b^2 - r^2))/b
eq1 = -b^2/a^2*x/y - (-(x - xx)/y)
eq2 = x^2/a^2 + y^2/b^2 - 1
eq3 = (x - xx)^2 + y^2 - r^2
eq4 = b + r - xx;

res = solve([eq2, eq3, eq4], (r, x, y))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (-800*b^3/2401 + b, -sqrt(49 - sqrt(2401 - 1600*b^2))*sqrt(sqrt(2401 - 1600*b^2) + 49)/20, b*sqrt(2401 - 1600*b^2)/49)
    (-800*b^3/2401 + b, sqrt(49 - sqrt(2401 - 1600*b^2))*sqrt(sqrt(2401 - 1600*b^2) + 49)/20, b*sqrt(2401 - 1600*b^2)/49)

2 組の解が得られる。本質的にはどちらでもよいが，当初の予想と同じ符号になる 2 番目のものを適解とする。
r として得られた解をプロットしてみると，b = 1 近辺で最大値になることがわかる。

r = res[2][1]
pyplot(size=(400, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(r, xlims=(0.95, 1.05), xlab="b", ylab="r")

r が最大になるのは b = 49*sqrt(6)/120 = 1.00020831163646 のときである。

b0 = solve(diff(res[1][1], b))[1]
(b0, b0.evalf()) |> println

   (49*sqrt(6)/120, 1.00020831163646)

b = 49*sqrt(6)/120 = 1.00020831163646 のときの r, x, y は以下の通りである。

r0 = res[2][1](b => b0)
x0 = res[2][2](b => b0)
y0 = res[2][3](b => b0)
(r0, x0, y0) |> println
(r0.evalf(), x0.evalf(), y0.evalf()) |> println

   (49*sqrt(6)/180, sqrt(49 - 49*sqrt(3)/3)*sqrt(49*sqrt(3)/3 + 49)/20, 49*sqrt(2)/120)
   (0.666805541090976, 2.00041662327293, 0.577470537969014)

その他のパラメータは以下の通り。

   a = 2.45;  b = 1.00021;  r = 0.666806;  xx = 2.00042;  x = 2.00042;  y = 0.577471

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 4.9/2
   b = 1.00020831163646
   (r, x, y) = (0.666805541090976, 2.00041662327293, 0.577470537969014)
   xx = sqrt((a^2 - b^2)*(b^2 - r^2))/b  # 1.67
   @printf("a = %g;  b = %g;  r = %g;  xx = %g;  x = %g;  y = %g\n", a, b, r, x0, x, y)
   plot()
   ellipse(0, 0, a, b, color=:red)
   ellipse(0, 0, b, a, color=:red)
   circle42(0, xx, r, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(xx, 0, "xx", :blue, :center, delta=-delta/2)
       point(x, y, "(x,y)", :blue, :left, :bottom, delta=delta/2)
       point(b, 0, "b  ", :red, :center, delta=-delta/2)
       point(a, 0, " a", :red, :center, delta=-delta/2)
   end
end;

算額（その636）

算額（その636）

長野県北佐久郡軽井沢町峠 熊野神社 文政11年(1828)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

楕円内に大円 2 個，小円 7 個が入っている。楕円の長径（差渡し）が 95 寸のとき，小円の直径はいかほどか。

楕円の長径と短径(差渡し)を 2a, 2b; b = 3r2
大円の半径と中心座標を r1, (0, r2)
小円の半径と中心座標を r2, (r1 + r2, r2)
右上の小円と楕円との接点座標を (x, y)
とおき，以下の連立方程式を解く。

なお，a も未知数として解く（結果の式に a が含まれる）事もできるが，一般性を失わずに a = 1 としてとき，結果を定数倍する（この場合 95/2 倍）こともできる。特にこの問題では結果の式がかなり複雑になるので a = 1 として解くという方針で進める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a::positive, b::positive, r1::positive, r2::positive,
     x::positive, y::positive

a = 1
b = 3r2
r1 = 2r2
x2 = 3r2
eq1 = -b^2/a^2*x/y - (-(x - x2)/(y - r2))
eq2 = x^2/a^2 + y^2/b^2 - 1
eq3 = (x - x2)^2 + (y - r2)^2 - r2^2;

res = solve([eq1, eq2, eq3], (r2, x, y))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    ((-5*sqrt(-37887 + 15468*sqrt(6))/8 - 3*sqrt(-25258 + 10312*sqrt(6))/4 + 9/8 + 4*sqrt(6)/3)/sqrt(-36 - sqrt(2)*sqrt(-12629 + 5156*sqrt(6)) + 79*sqrt(6)), (-2*sqrt(-37887 + 15468*sqrt(6))/5 - 2*sqrt(-25258 + 10312*sqrt(6))/5 + 2/5 + 22*sqrt(6)/5)/sqrt(-36 - sqrt(2)*sqrt(-12629 + 5156*sqrt(6)) + 79*sqrt(6)), sqrt(-27/800 - 3*sqrt(2)*sqrt(-12629 + 5156*sqrt(6))/3200 + 237*sqrt(6)/3200))
    ((3*sqrt(-25258 + 10312*sqrt(6))/4 + 5*sqrt(-37887 + 15468*sqrt(6))/8 + 9/8 + 4*sqrt(6)/3)/sqrt(-36 + sqrt(2)*sqrt(-12629 + 5156*sqrt(6)) + 79*sqrt(6)), (2/5 + 2*sqrt(-25258 + 10312*sqrt(6))/5 + 2*sqrt(-37887 + 15468*sqrt(6))/5 + 22*sqrt(6)/5)/sqrt(-36 + sqrt(2)*sqrt(-12629 + 5156*sqrt(6)) + 79*sqrt(6)), sqrt(-27/800 + 3*sqrt(2)*sqrt(-12629 + 5156*sqrt(6))/3200 + 237*sqrt(6)/3200))

2 組の解が得られるが，最初のものが適解である。

r2 の式はさほど長くはないが，短くすることはできる。多少の誤差は浮動小数点演算のせいである（多倍精度演算するとおなじになる）。

res[1][1] |> println

   (-5*sqrt(-37887 + 15468*sqrt(6))/8 - 3*sqrt(-25258 + 10312*sqrt(6))/4 + 9/8 + 4*sqrt(6)/3)/sqrt(-36 - sqrt(2)*sqrt(-12629 + 5156*sqrt(6)) + 79*sqrt(6))

term = sqrt(5156√big"6" - 12629)
e1 = (-5√3term/8 - 3√2term/4 + 9/8 + 4√6/3)/sqrt(-36 - √2term + 79√6)
e1

   0.2217968134779909378691753768002565302883462091899984084765888265892542449509785

res[1][1].evalf() |> println

   0.221796813477991

a = 95/2 のとき，結果をすべて a 倍する。
小円の直径 = 2*(95/2)*0.221796813477991　= 21.070697280409146

2*(95/2)*0.221796813477991

   21.070697280409146

その他のパラメータは以下の通りである。

a = 47.5;  b = 31.606;  r1 = 21.0707;  x2 = 10.5353;  x = 38.8437;  y = 18.191

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, x, y) = 95//2 .* (
       (-5*sqrt(-37887 + 15468*sqrt(6))/8 - 3*sqrt(-25258 + 10312*sqrt(6))/4 + 9/8 + 4*sqrt(6)/3)/sqrt(-36 - sqrt(2)*sqrt(-12629 + 5156*sqrt(6)) + 79*sqrt(6)),
       (-2*sqrt(-37887 + 15468*sqrt(6))/5 - 2*sqrt(-25258 + 10312*sqrt(6))/5 + 2/5 + 22*sqrt(6)/5)/sqrt(-36 - sqrt(2)*sqrt(-12629 + 5156*sqrt(6)) + 79*sqrt(6)),
       sqrt(-27/800 - 3*sqrt(2)*sqrt(-12629 + 5156*sqrt(6))/3200 + 237*sqrt(6)/3200))
   a = 95/2
   b = 3r2
   r1 = 2r2
   x2 = 3r2
   @printf("小円の直径 = %.15g\n", 2r2)
   @printf("a = %g;  b = %g;  r1 = %g;  r2 = %g;  x2 = %g;  x = %g;  y = %g\n",
       a, b, r1, r2, x2, x, y)
   plot()
   ellipse(0, 0, a, b, color=:red)
   circle(0, b - 2r2, 2r2, :magenta)
   circle(0, 2r2 - b, 2r2, :magenta)
   circle(0, 2r2, r2, :blue)
   circle(0, -2r2, r2, :blue)
   circle(0, 0, r2, :blue)
   circle4(x2, r2, r2, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x, y, "(x,y)", :red, :left, :bottom)
       point(3r2, r2, "(3r2,r2)", :blue, :center, delta=-delta/2)
       point(0, b, " b", :red, :left, :bottom, delta=delta/2)
       point(a, 0, "a ", :red, :right, :bottom, delta=delta/2)
   end
end;

算額（その635）

算額（その635）

算額（その360）と同じ図形

埼玉県加須市騎西 玉敷神社 大正4年(1915)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

東京都中央区日本橋 福徳神社（芽吹稲荷）
https://mebuki.jp/2125/
玉敷神社に奉納された算額中の問題を復元したもの。

甲円 2 個と 2 本の直線と 2 個の乙円がある。甲円の直径を 3 とするとき，乙円の直径を求めよ。

算額（その628）を単純化したもの。
三角形の底辺の長さを 2a とする。
甲円の半径と中心座標を r1, (0, r1), (0, 3r1)
乙円の半径と中心座標を r2, (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r1::positive, r2::positive, x2::positive, y2::positive, a::positive

sinθ = r1/3r1
#eq1 = (4r1 - (2r1 + r3))sinθ - r3
eq2 = a/sqrt((4r1)^2 + a^2) - sinθ
eq3 = r1*sinθ - (r1 - 2r2)
eq4 = x2^2 + (y2 - 3r1)^2 - (r1 - r2)^2
eq5 = (y2 - 3r1)/x2 *(-4r1)/a + 1;

res = solve([eq2, eq3, eq4, eq5], (a, r2, x2, y2))

   1-element Vector{NTuple{4, Sym}}:
    (sqrt(2)*r1, r1/3, 4*sqrt(2)*r1/9, 29*r1/9)

乙円の直径は甲円の直径の 1/3 倍である。
甲円の直径が 3 寸のとき，乙円の直径は 1 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 3//2
   (a, r2, x2, y2) = r1 .* (√2, 1/3, 4√2/9, 29/9)
   @printf("乙円の直径 = %g\n", 2r2)
   @printf("a = %g;  r1 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n", a, r1, r2, x2, y2)
   plot([a, 0, -a, 0], [0, 4r1, 0, 0], color=:orange, lw=0.5)
   circle(0, r1, r1)
   circle(0, 3r1, r1)
   circle(x2, y2, r2, :blue)
   circle(-x2, y2, r2, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, r1, " 甲円:r1,(0,r1)", :red, :left, :vcenter)
       point(0, 3r1, " 3r1", :red, :left, :vcenter)
       point(x2, y2, "乙円:r2\n(x2,y2)", :blue, :center, :top, delta=-delta/2)
       point(a, 0, "a", :black, :left, :bottom, delta=delta)
       point(0, 4r1, " 4r1", :black, :left, :bottom)
   end
end;

算額（その634）

算額（その634）

埼玉県加須市馬内 秋葉神社

東京都中央区日本橋 福徳神社（芽吹稲荷）
https://mebuki.jp/2125/

埼玉県加須市馬内の秋葉神社に奉納された算額中の問題を復元したもの。

大円の中に上円，中円，下円が円に接する 2 本の直線に挟まれている。上円，下円の直径を 16，64 とするとき，外円の直径を求めよ。

外円の半径と中心座標を R, (0, 0)
上円の半径と中心座標を r1, (r1, y1)
中円の半径と中心座標を r2, (0, y2)
下円の半径と中心座標を r3, (r3, y3)
2直線の交点は y 軸上にあり，その座標を (0, a) とする。
描かれる図形の正しさを保証する座標として，直線と外円との交点座標を (x, sqrt(R^2 - x^2)) とする。
以下の連立方程式を解く。
直線と y 軸のなす角を 2θ，(0, a) と下円の中心座標 (r3, y3) がなす角は θ で，tan(2θ) と tan(θ) の関係式が連立方程式 eq6 である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a::positive, R::positive, r1::positive, y1::positive,
     r2::positive, y2::positive, r3::positive, y3::negative,
     x::positive
eq1 = r1^2 + y1^2 - (R - r1)^2
eq2 = r1^2 + (y1 - y2)^2 - (r1 + r2)^2
eq3 = r3^2 + y3^2 - (R - r3)^2
eq4 = r3^2 + (y3 - y2)^2 - (r2 + r3)^2
eq5 = r1/(a - y1) - r3/(a - y3)
tanθ = r1/(a - y1)
tan2θ = r2/sqrt((a - y2)^2 - r2^2)
eq6 = tan2θ - 2tanθ/(1 - tanθ^2)  # tan の倍角公式
eq7 = x/(a + sqrt(R^2 - x^2)) - tan2θ;  # 外円との交点

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (a, R, y1, r2, y2, y3, x) = u
   return [
       r1^2 + y1^2 - (R - r1)^2,  # eq1
       r1^2 - (r1 + r2)^2 + (y1 - y2)^2,  # eq2
       r3^2 + y3^2 - (R - r3)^2,  # eq3
       r3^2 - (r2 + r3)^2 + (-y2 + y3)^2,  # eq4
       r1/(a - y1) - r3/(a - y3),  # eq5
       -2*r1/((a - y1)*(-r1^2/(a - y1)^2 + 1)) + r2/sqrt(-r2^2 + (a - y2)^2),  # eq6
       -r2/sqrt(-r2^2 + (a - y2)^2) + x/(a + sqrt(R^2 - x^2)),  # eq7
   ]
end;

(r1, r3) = (16, 64).//2
iniv = BigFloat[100, 75, 70, 35, 25, -30, 70]
res = nls(H, ini=iniv)

   (BigFloat[101.0160878276326834706245414713648871161063810216537006427555673980074763401048, 76.49999999999999999999999999999999999999999999999999999999762230488260311415535, 68.03124282269139907205326262357227091492878721866473716757506133442061889385097, 33.99999999999999999999999999999999999999999999999999999999738290330058695649773, 26.80018656651479357383916406383150066345679496492853282359138444046472151565239, -30.9232921921324541236605739198055776886039941903021532579865373591499745691432, 69.04228072652930803351703141806364055524282066404273049867895237707748909712568], true)

外円の直径 = 153;  a = 101.0160878;  R = 76.5;  y1 = 68.0312;  r2 = 34;  y2 = 26.8002;  y3 = -30.9233

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3) = (16, 64) .// 2
   (a, R, y1, r2, y2, y3) = (230, 160, 140, 75, 50, -70) .// 2
   (a, R, y1, r2, y2, y3, x) = res[1]
   @printf("外円の直径 = %g;  a = %.10g;  R = %g;  y1 = %g;  r2 = %g;  y2 = %g;  y3 = %g\n", 2R, a, R, y1, r2, y2, y3)
   plot()
   circle(0, 0, R)
   circle(r1, y1, r1, :blue)
   circle(-r1, y1, r1, :blue)
   circle(0, y2, r2, :green)
   circle(r3, y3, r3, :magenta)
   circle(-r3, y3, r3, :magenta)
   segment(0, a, x, -sqrt(R^2 - x^2), :orange)
   segment(0, a, -x, -sqrt(R^2 - x^2), :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:gray80, lw=0.5)
       hline!([0], color=:gray80, lw=0.5)
       point(0, a, " a", :black, :left, :vcenter)
       point(x, -sqrt(R^2-x^2), "(x,-√(R^2-x^2)) ", :black, :right, delta=-delta)
       point(r1, y1, " 上円:r1,(r1,y1)", :blue, :left, :vcenter)
       point(0, y2, " 中円:r2\n (0,y2)", :green, :left, :vcenter)
       point(r3, y3, "下円:r3,(r3,y3)", :magenta, :center, :bottom, delta=delta/2)
   end
end;

算額（その633）

算額（その633）

一〇五 加須市騎西町中種足 雷神社 大正元年(1912)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

東京都中央区日本橋 福徳神社（芽吹稲荷）
https://mebuki.jp/2125/

正方形の中に対角線と小さい正方形，正三角形と大小の円がある。小円の直径を 1 とするとき，大円の直径を求めよ。

正方形の一辺の長さを a とする。x 軸にある正三角形の頂点の座標を (x, 0) とする。
大円，小円の半径を r1, r2 として，まず x を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms l::positive, a::positive, x::positive, r1::positive, r2::positive
eq1 = (x - a/2)^2 +(a/2)^2 - 2(a - x)^2
res = solve(eq1, x);
res |> println
res[1](a => 1).evalf(),res[2](a => 1).evalf()

   Sym[a*(3 - sqrt(3))/2, a*(sqrt(3) + 3)/2]

   (0.633974596215561, 2.36602540378444)

解が 2 個求められるが，最初のものが適解である。
x = a*(3 - √3)/2

x = res[1]
x |> println

   a*(3 - sqrt(3))/2

正三角形の一辺の長さ l は √2(a - x) である。

l = sqrt(Sym(2))*(a - x)
l |> println

   sqrt(2)*(-a*(3 - sqrt(3))/2 + a)

大円，小円は（二等辺）直角三角形に内接しているので，「鈎股弦中の円の直径」公式により求められる。

r1 = (2(a/2) - (a/2)*sqrt(Sym(2)))/2
r2 = (2(a - x) - l)/2
r1 |> println
r2 |> println

   -sqrt(2)*a/4 + a/2
   -a*(3 - sqrt(3))/2 + a - sqrt(2)*(-a*(3 - sqrt(3))/2 + a)/2

r2 を 1 としたときの r1 は，(-sqrt(2)*a/4 + a/2)/(-a*(3 - sqrt(3))/2 + a - sqrt(2)*(-a*(3 - sqrt(3))/2 + a)/2) のようになるが，これは簡約化すると 1/2 + sqrt(3)/2 = (1 + √3)/2 = 1.36602540378444 になる。

ratio = r1/r2
ratio |> println
apart(ratio) |> simplify |> println
ratio.evalf() |> println

   (-sqrt(2)*a/4 + a/2)/(-a*(3 - sqrt(3))/2 + a - sqrt(2)*(-a*(3 - sqrt(3))/2 + a)/2)
   1/2 + sqrt(3)/2
   1.36602540378444

小円の直径を 1 とするとき，大円の直径は約 1.366 である。

その他のパラメータは以下の通りである。

a = 1;  x = 0.633975;  l = 0.517638;  r1 = 0.146447;  r2 = 0.107206;  r1/r2 = 1.36603

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 1
   x = a*(3 - √3)/2
   l = √2*(a - x)
   r1 = (2(a/2) - (a/2)√2)/2
   r2 = (2(a - x) - l)/2
   @printf("a = %.10g;  x = %g;  l = %g;  r1 = %g;  r2 = %g;  r1/r2 = %g\n", a, x, l, r1, r2, r1/r2)
   plot()
   rect(0, 0, a, a, :black)
   rect(0, a/2, a/2, a, :blue)
   segment(0, 0, a, a, :black)
   plot!([a/2, x, a, a/2], [a/2, 0, a - x, a/2], color=:orange, lw=0.5)
   circle(r1, a/2 - r1, r1,)
   circle(a/2 + r1, a - r1, r1,)
   circle(a - r2, r2, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       # vline!([0], color=:gray80, lw=0.5)
       # hline!([0], color=:gray80, lw=0.5)
       point(0, a/2, " a/2", :black, :left, :bottom, delta=delta/2)
       point(0, a, " a", :black, :left, :bottom, delta=delta/2)
       point(a/2, a/2, "(a/2,a/2) ", :black, :right, :bottom, delta=delta/2)
       point(x, 0, "x ", :black, :right, :bottom, delta=delta/2)
       point(a, 0, "a ", :black, :right, :bottom, delta=delta/2)
       point(a/2, a, "(a/2,a)", :black, :center, :bottom, delta=delta/2)
       point(a, a - x, "(a,a-x)  ", :black, :right, :vcenter)
       point(r1, a/2 - r1, "大円:r1\n(r1,a/2-r1)", :red, :center, delta=-delta/2)
       point(a/2 + r1, a - r1, "大円:r1\n(a/2+r1,a-r1)", :red, :center, delta=-delta/2)
       point(a - r2, r2, "小円:r2\n(a-r2,r2)", :green, :center, delta=-delta/2)
   end
end;

算額（その629）

算額（その629）

和算図形問題あれこれ
令和4年5月の問題-No.1
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

正方形内に正六角形を入れる。正方形の一辺の長さが 1219 寸のとき，正六角形の一辺の長さはいかほどか。

正方形の一辺の長さを a とする。b，c を図のように定義し，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms l::positive, a::positive, b::positive, c::positive

eq0 = 2(a/2 - c)^2 - l^2
eq1 = (a/2)^2 + (b - a/2)^2 - l^2
eq2 = c^2 + (b - c)^2 - l^2
res = solve([eq0, eq1, eq2], (l, b, c))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (a*sqrt(2 - sqrt(3)), -sqrt(3)*a/2 + 3*a/2, a*(1 - sqrt(3)/2))
    (a*sqrt(sqrt(3) + 2), sqrt(3)*a/2 + 3*a/2, a*(sqrt(3)/2 + 1))

最初のものが適解である。

正六角形の一辺の長さは a*sqrt(2 - sqrt(3)) = a√(2 - √3) である。

正方形の一辺の長さ a が 1219 寸のとき，正六角形の一辺の長さは a√(2 - √3) = 631.0008319599457 寸である。

a = 1219
a√(2 - √3)

   631.0008319599457

その他のパラメータは以下の通り。

a = 1219;  b = 772.815;  c = 163.315

function draw(more=false)
   pyplot(size=(300, 300), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 1219
   (l, b, c) = (a*sqrt(2 - sqrt(3)), -sqrt(3)*a/2 + 3*a/2, a*(1 - sqrt(3)/2))
   @printf("正六角形の一辺の長さ = %g;  a = %g;  b = %g;  c = %g\n", l, a, b, c)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:cyan, lw=0.5, seriestype=:shape, alpha=0.5)
   plot!([c, b, a, a - c, a - b, 0, c], [c, 0, a - b, a - c, a, b, c], color=:orange, lw=0.5, seriestype=:shape, alpha=0.8)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(a, 0, "a ", :black, :right, :bottom, delta=delta/2)
       point(c, c, "(c,c)", :black, :left, :bottom, delta=delta/2)
       point(0, b, " b", :black, :left, :vcenter)
   end
end;

算額（その632）

算額（その632）

和算図形問題あれこれ
令和3年11月の問題2
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

直角三角形の中に，正三角形と等円 2 個を入れる。股の長さが 487 寸のとき，正三角形の一辺の長さはいかほどか。

正三角形の一辺の長さを a とする。
等円の半径と中心座標を r, (x, r), (r, y)
とおき，以下の連立方程式を解く

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r::positive, x::positive, y::positive, a::positive,
     鈎::positive, 股::positive
eq1 = distance(0, 0, a/2, sqrt(Sym(3))a/2, r, y) - r^2
eq2 = distance(a, 0, a/2, sqrt(Sym(3))a/2, x, r) - r^2
eq3 = distance(0, 鈎, 股, 0, r, y) - r^2
eq4 = distance(0, 鈎, 股, 0, x, r) - r^2
eq5 = (sqrt(Sym(3))a/2)/(股 - a/2) - 鈎/股;
# res = solve([eq1, eq2, eq3, eq4, eq5], (r, x, y, a, 鈎))

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r, x, y, a, 鈎) = u
   return [
       -r^2 + (3*r/4 - sqrt(3)*y/4)^2 + (-sqrt(3)*r/4 + y/4)^2,  # eq1
       -r^2 + (r - sqrt(3)*(a + sqrt(3)*r - x)/4)^2 + (-3*a/4 + sqrt(3)*r/4 + 3*x/4)^2,  # eq2
       -r^2 + (r - 股*(r*股 - y*鈎 + 鈎^2)/(股^2 + 鈎^2))^2 + (y - 鈎*(-r*股 + y*鈎 + 股^2)/(股^2 + 鈎^2))^2,  # eq3
       -r^2 + (r - 鈎*(r*鈎 - x*股 + 股^2)/(股^2 + 鈎^2))^2 + (x - 股*(-r*鈎 + x*股 + 鈎^2)/(股^2 + 鈎^2))^2,  # eq4
       sqrt(3)*a/(2*(-a/2 + 股)) - 鈎/股,  # eq5
   ]
end;

股 = 487
iniv = BigFloat[56, 295, 209, 263, 312]
res = nls(H, ini=iniv

   (BigFloat[56.11416043991601035847741706383402473599898003302003798949966598270036579889394, 295.3980059252043265908683636932107368735334613723332636723610589520722219482431, 209.4208977858381008824304265789438848352208122172291274041824122497419576667868, 263.0004802898689700383037446882855378574200007464121970616614846371699418629093, 312.0159697201720972932632403222578260473761673054778157588165017227055663499631], true)

股の長さが 487 寸のとき，正三角形の一辺の長さはほぼ 263 寸である。

その他のパラメータは以下の通り。
r = 56.1142;  x = 295.398;  y = 209.421;  a = 263;  鈎 = 312.016

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   股 = 487
   (r, x, y, a, 鈎) = res[1]
   @printf("正三角形の一辺の長さ = %.10g;  r = %g;  x = %g;  y = %g;  a = %g;  鈎 = %g\n", a, r, x, y, a, 鈎)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:gray80, lw=0.5)
   plot!([0, a, a/2, 0], [0, 0, √3a/2, 0], color=:gray80, lw=0.5)
   circle(r, y, r, :blue)
   circle(x, r, r, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:gray80, lw=0.5)
       hline!([0], color=:gray80, lw=0.5)
       point(a/2, √3a/2, "(a/2,√3a/2)")
       point(x, r, "(x,r)", :blue, :center, delta=-delta/2)
       point(r, y, "(r,y)", :blue, :center, delta=-delta/2)
       point(股, 0, "股", :black, :left, :bottom, delta=delta/2)
       point(a, 0, "a ", :black, :right, :bottom, delta=delta/2)
       point(0, 鈎, "鈎", :black, :left, :bottom, delta=delta/2)
   end
end;

算額（その631）

算額（その631）

和算図形問題あれこれ
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

長方形の中に，菱形，大円 2 個，小円 4 個が入っている。小円は長方形に内接し，大円，菱形に外接している。大円は互いに外接し，長方形に内接し，小円に外接している。算額の図では大円は互いに接していないように見えるが，実際は接している。
長方形の短辺の長さが 2 寸 5 分のとき小円の直径はいかほどか。

長方形の長辺，短辺の長さを 2a, 2b とする。
大円の半径と中心座標を r1, (0, r1); r = b/2
小円の半径と中心座標を r2, ((a - r2, b - r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a::positive, b::positive, r1::positive, r2::positive
r1 = b//2
eq1 = (a - r2)^2 + (b - r2 - r1)^2 - (r1 + r2)^2
eq2 = distance(a, 0, 0, b, a - r2, b - r2) - r2^2
res = solve([eq1, eq2], (a, r2))

   1-element Vector{Tuple{Sym, Sym}}:
    (b*(5 + 3*sqrt(17))/16, b*(9 - sqrt(17))/16)

長方形の長辺の長さは b(5 + 3√17)/8，小円の直径は b(9 - √17)/8 である。
長方形の短辺の長さが 2 寸 5 分のとき，長辺の長さは 2 寸 7 分 1 厘 4 毛ほど，小円の直径は 7 分 6 厘 2 毛ほどである。

b = 2.5/2
b .* ((5 + 3√17)/8, (9 - √17)/8)

   (2.713955762008278, 0.7620147459972405)

その他のパラメータは以下の通り。

b = 1.25;  r1 = 0.625;  r2 = 0.381007

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   b = 2.5/2
   r1 = b/2
   (a, r2) = (25/64 + 15*sqrt(17)/64, 45/64 - 5*sqrt(17)/64)
   @printf("小円の直径 = %g;  b = %g;  r1 = %g;  r2 = %g\n", 2r2, b, r1, r2)
   plot([a, a, -a, -a, a], [-b, b, b, -b, -b], color=:gray80, lw=0.5)
   plot!([a, 0, -a, 0, a], [0, b, 0, -b, 0], color=:gray80, lw=0.5)
   circle4(a - r2, b - r2, r2)
   circle(0, r1, r1, :blue)
   circle(0, -r1, r1, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:gray80, lw=0.5)
       hline!([0], color=:gray80, lw=0.5)
       point(0, r1, " 大円:r1\n (0,r1)", :blue, :left, :vcenter)
       point(a - r2, b - r2, " 小円:r2\n (a-r2,b-r2)", :red, :center, delta=-delta/2)
       point(0, b, " b", :black, :left, :bottom, delta=delta/2)
       point(a, 0, " a", :black, :left, :vcenter)
   end
end;

算額（その630）

算額（その630）

和算図形問題あれこれ
令和4年8月の問題-No.1
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

正三角形内に斜線を 3 本引き，分割された領域に直径が 1174 寸の等円を 3 個入れる。正三角形の一辺の長さを求めよ。

正三角形の一辺の長さを 2a とする。
等円の半径と中心座標を r, (x, r), (0, 3r)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a::positive, b::positive, x::positive, r::positive

r = 1174//2
eq1 = r/(a - x) - 1/sqrt(Sym(3))
三角形の相似から x を求める
r2 = sqrt(Sym(3))a - 2r  # 三角形の頂点から真ん中の等円の下端までの距離
r3 = sqrt(Sym(3))a - 3r  # 三角形の頂点から真ん中の等円の中心までの距離
eq2 = 2r*r2/sqrt(r3^2 - r^2) - x
eq3 = r/r3 - b/sqrt(3a^2 + b^2);
res = solve([eq1, eq2, eq3], (a, b, x))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (587*sqrt(11)/2 + 1761*sqrt(3)/2, 587*sqrt(3), 587*sqrt(3)/2 + 587*sqrt(11)/2)

res[1][1] |> factor |> println

   587*(sqrt(11) + 3*sqrt(3))/2

正三角形の一辺の長さは 2a = (√11 + 3√3)*等円直径/2 = 4997.000224067413 である。

(√11 + 3√3)*1174/2 |> println

   4997.000224067413

正三角形の一辺の長さ = 4997.000224;  等円の直径 = 1174
a = 2498.5;  b = 1016.71;  x = 1481.79

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1174//2
   (a, b, x) = (587*sqrt(11)/2 + 1761*sqrt(3)/2, 587*sqrt(3), 587*sqrt(3)/2 + 587*sqrt(11)/2)
   @printf("正三角形の一辺の長さ = %.10g;  等円の直径 = %g;  a = %g;  b = %g;  x = %g\n", 2a, 2r, a, b, x)
   plot()
   vline!([0], color=:gray80, lw=0.5)
   hline!([0], color=:gray80, lw=0.5)
   plot!([a, 0, -a, a], [0, √3a, 0, 0], color=:green, lw=0.5)
   circle(x, r, r)
   circle(0, 3r, r)
   c = (√3a - 2r)/√3
   segment(0, √3a, b, 0, :blue)
   segment(0, √3a, -b, 0, :blue)
   segment(-c, 2r, c, 2r, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       point(0, 3r, " 3r", :red, :left, :vcenter)
       point(x, r, "(x,r)", :red, :center, delta=-delta/2)
       point(0, √3a, " √3a", :black, :left, :vcenter)
       point(a, 0, "a", :blue, :center, delta=-delta)
       point(b, 0, "b", :blue, :center, delta=-delta)
       plot!(ylims=(-300, √3a+100))
   end
end;

 

算額（その628）

算額（その628）

和算図形問題あれこれ
令和3年12月の問題2
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

二等辺三角形の内外に甲円 2 個を置き，その間に乙円，丙円，丁円を入れる。甲円の直径が 6寸のとき，乙円，丙円，丁円の直径と三角形の底辺の長さを求めよ。

三角形の底辺の長さを 2a とする。
甲円の半径と中心座標を r1, (0, r1), (0, 3r1)
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (0, 2r1 + r3)
丁円の半径と中心座標を r4, (x4, y4)
とおき，以下の連立方程式を解く。

SymPy の能力上，まとめて解くことができないようなので，最初に独立な 3 変数の解を求め，続いてそれらが既知として残りのパラメータを求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r1::positive, r2::positive, x2::positive, y2::positive, a::positive, r3::positive, r4::positive, x4::positive, y4::positive

sinθ = r1/3r1
eq1 = (4r1 - (2r1 + r3))sinθ - r3
eq2 = a/sqrt((4r1)^2 + a^2) - sinθ
eq3 = r1*sinθ - (r1 - 2r2);

res1 = solve([eq1, eq2, eq3], (a, r2, r3))

   Dict{Any, Any} with 3 entries:
     r3 => r1/2
     a  => sqrt(2)*r1
     r2 => r1/3

乙円，丙円の直径，底辺の長さは甲円の直径の 1/3，1/2， √2 倍である。
甲円の直径が 6 寸のとき，乙円，丙円の直径は 2 寸，3 寸である。底辺の長さは 6√2 ≒ 8.48528 寸である。

@syms r1::positive, r2::positive, x2::positive, y2::positive, a::positive, r3::positive, r4::positive, x4::positive, y4::positive

(a, r2, r3) = r1 .* (sqrt(Sym(2)), 1//3, 1//2)
eq4 = x4^2 + (3r1 - y4)^2 - (r1 + r4)^2
eq5 = x4^2 + (y4 - r1)^2 - (r1 + r4)^2
eq6 = distance(0, 4r1, a, 0, x4, y4) - r4^2
eq7 = x2^2 + (y2 - 3r1)^2 - (r1 - r2)^2
eq8 = (y2 - 3r1)/x2 *(-4r1)/a + 1
res2 = solve([eq4, eq5, eq6, eq7, eq8], (x2, y2, r4, x4, y4))

   2-element Vector{NTuple{5, Sym}}:
    (4*sqrt(2)*r1/9, 29*r1/9, 2*r1, 2*sqrt(2)*r1, 2*r1)
    (4*sqrt(2)*r1/9, 29*r1/9, 2*r1*(7 - 4*sqrt(3)), -2*sqrt(2)*r1*(35 - 21*sqrt(3))/7, 2*r1)

2 番目のものが適解である。

丁円の直径は甲円の直径の 2(7-4√3) 倍である。
甲円の直径が 6 寸のとき，丁円の直径は 6*2(7-4√3) ≒ 0.861561 である。

乙円の直径 = 2;  丙円の直径 = 3; 丁円の直径(12(7-4√3)) = 0.861561;  底辺(6√2) = 8.48528

その他のパラメータは以下の通り。
a = 4.24264;  r1 = 3;  r2 = 1;  r3 = 1.5;  r4 = 0.430781;  x2 = 1.88562;  y2 = 9.66667; x4 = 1.66441;  y4 = 6

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 6//2
   (a, r2, r3) = r1 .* (sqrt(Sym(2)), 1//3, 1//2)
   (x2, y2, r4, x4, y4) = r1 .* (4*sqrt(2)/9, 29/9, 2(7 - 4*sqrt(3)), -2*sqrt(2)*(35 - 21*sqrt(3))/7, 2)
   @printf("乙円の直径 = %g;  丙円の直径 = %g; 丁円の直径 = %g;  底辺 = %g\n", 2r2, 2r3, 2r4, 2a)
   @printf("a = %g;  r1 = %g;  r2 = %g;  r3 = %g;  r4 = %g;  x2 = %g;  y2 = %g; x4 = %g;  y4 = %g\n", a, r1, r2, r3, r4, x2, y2, x4, y4)
   plot([a, 0, -a, 0], [0, 4r1, 0, 0], color=:orange, lw=0.5)
   circle(0, r1, r1)
   circle(0, 3r1, r1)
   circle(0, 2r1 + r3, r3, :blue)
   circle(x2, y2, r2, :green)
   circle(-x2, y2, r2, :green)
   circle(x4, y4, r4, :black)
   circle(-x4, y4, r4, :black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, r1, " 甲円:r1,(0,r1)", :red, :left, :vcenter)
       point(0, 3r1, " 3r1", :red, :left, :vcenter)
       point(x2, y2, "乙円:r2\n(x2,y2)", :green, :center, :top, delta=-delta/2)
       point(0, 2r1 + r3, " 丙円:r3\n (0,2r1+r3)", :blue, :left, :vcenter)
       point(x4, y4, " 丁円:r4,(x4,y4)", :black, :left, :vcenter)
       point(a, 0, "a", :black, :left, :bottom, delta=delta)
       point(0, 4r1, " 4r1", :black, :left, :bottom)
   end
end;

算額（その627）

算額（その627）

和算図形問題あれこれ
令和4年9月の問題-No.2
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

大球の中に甲球 2 個と乙球 5 個が入っている。甲球は交差しており，乙球の 1 個が交差部分に内接している。残りの 4 個の乙球は甲球と外接し大球に内接している。
甲球の直径が 987 寸のとき，乙球の直径はいかほどか。

図は，3次元空間を Z 軸方向上方から見たものであり，中央の乙球は手前と奥を含めて 3 個が一直線上に並んでいる。図の上下の乙球と甲球は x-y 平面上(z = 0）に中心を持つ。

大球の半径と中心座標を R, (0, 0)
甲球の半径と中心座標を r1, (R - r1, 0)
乙球の半径と中心座標を r2, (0, R - r2)
とおき，以下の連立方程式を解き，大球，乙球の半径を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms R, r1, r2

r1 = 987//2
eq1 = (2r1 - r2) - R
eq2 = (R - r1)^2 + (R - r2)^2 - (r1 + r2)^2
res = solve([eq1, eq2], (R, r2))

   2-element Vector{Tuple{Sym, Sym}}:
    (987/4 - 987*sqrt(5)/4, 987*sqrt(5)/4 + 2961/4)
    (987/4 + 987*sqrt(5)/4, 2961/4 - 987*sqrt(5)/4)

2 番目のものが適解である。

R = 987/4 + 987*sqrt(5)/4
r2 = 2961/4 - 987*sqrt(5)/4
(R, r2)

   (798.4997734480731, 188.50022655192686)

r2 はほんの少しだけ簡約化できる。

res[2][2] |> factor |> println

   -987*(-3 + sqrt(5))/4

987(3 - √5)/4, 987(3 - √5)/2

   (188.50022655192686, 377.0004531038537)

乙球の直径は 987(3 - √5)/2 = 377.0004531038537 である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 987//2
   R = 987/4 + 987*sqrt(5)/4
   r2 = 2961/4 - 987*sqrt(5)/4
   @printf("乙球の直径 = %g;  R = %g; r2 = %g;  r1 = %g\n", 2r2, R, r2, r1)
   plot()
   circle(0, 0, R, :black)
   circle(R - r1, 0, r1, :blue)
   circle(r1 - R, 0, r1, :blue)
   circle(0, 0, r2)
   circle(0, R - r2, r2)
   circle(0, r2 - R, r2)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(R - r1, 0, "甲球:r1", :blue, :center, delta=-delta/2)
       point(0, R - r2, "乙球:r2", :red, :left, :vcenter)
       point(R, 0, "R ", :black, :right, delta=-delta/2)
   end
end;

 

算額（その626）

算額（その626）

和算図形問題あれこれ
令和4年9月の問題-No.1
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

左右対称の四角形の中に，正方形と 2 斜線がある。赤，黃，黒の面積が 12 平方寸, 24 平方寸，16 平方寸のとき，正方形の一辺の長さはいかほどか。

頂点などの座標を図のように定義する。直線の上にある（ように見える）点はまさに直線上にある（傾きの同じ直線上にある）という 4 条件と，赤，黃，黒の面積の 3 条件についての連立方程式を解く。

SymPy での計算は分数式で行われるので，誤差が含まれるおそれはない。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a::positive, b::positive, c::positive,
     d::positive, e::positive,
     x::positive, y::positive
     R::positive, Y::positive, K::positive

(R, Y, K) = (12, 24, 16)
eq1 = (y - c)/x - ((d + 2a) - c)/a
eq2 = (y - b)/x - (y - e)/(x - a)
eq3 = (y - e)/(x - a) - (y - (d + 2a))/(x + a)
eq4 = y/x - (y - d)/(x - a)
eq5 = ((d + 2a) - e)a - R
eq6 = (e - d) * (x - a) - Y
eq7 = (c - (d + 2a))a - K;

res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7])

   1-element Vector{Dict{Any, Any}}:
    Dict(x => 44/5, y => 88/15, b => 55/6, d => 8/3, e => 23/3, c => 44/3, a => 4)

a = 4 になるので，正方形の一辺の長さは 2a = 8 である。

その他のパラメータは以下の通り。

a = 4//1;  b = 55//6;  c = 44//3;  d = 8//3;  e = 23//3;  x = 44//5; y = 44//5

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   x = 44//5; y = 88//15; b = 55//6; d = 8//3; e = 23//3; c = 44//3; a = 4//1
   println("a = $a;  b = $b;  c = $c;  d = $d;  e = $e;  x = $x; y = $x")
   println("赤: $((d + 2a - e)a)")
   println("黃: $((e - d)*(x - a))")
   println("黒: $((c - (d + 2a))a)")
   plot([x, 0, -x, 0, x],  [y, c, y, 0, y], color=:black, lw=0.5)
   plot!([a, a, -a, -a, a], [d, d + 2a, d + 2a, d, d], color=:black, lw=0.5)
   plot!([0, a, a, 0], [b, d + 2a, e, b], color=:red, seriestype=:shape, alpha=0.4)
   plot!([0, -a, -a, 0], [b, d + 2a, e, b], color=:red, seriestype=:shape, alpha=0.4)
   plot!([a, x, a, a], [e, y, d, e], color=:yellow, seriestype=:shape, alpha=0.4)
   plot!([-a, -x, -a, -a], [e, y, d, e], color=:yellow, seriestype=:shape, alpha=0.4)
   plot!([0, a, -a, 0], [c, d + 2a, d + 2a, c], color=:black, seriestype=:shape, alpha=0.2)
   segment(x, y, -a, d + 2a)
   segment(-x, y, a, d + 2a)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(a, d + 2a, " (a,d+2a)", :black, :left, :vcenter)
       point(a, e, " (a,e)", :black, :left, :bottom, delta=delta/2)
       point(x, y, " (x,y)", :black, :left, :vcenter)
       point(a, d, " (a,d)", :black, :left, delta=-delta/2)
       point(0, b, " b", :black, :left, delta=-delta)
       point(0, c, " c", :black, :left, :vcenter)
       point(0, d, " d", :black, :left, delta=-delta)
   end
end;

算額（その625）

算額（その625）

和算図形問題あれこれ
令和4年10月の問題-No.1
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

直角三角形の面積を縦線で n 等分する。甲の長さが a 寸であるとき，乙の長さを n と a で表わせ。また，n = 10，a = 419 のときの 乙の長さを求めよ。

底辺を n 個に区分する分点を w[1], w[2], ..., w[n-2], w[n-1], w[n] とする。
原点 w[0], からそれぞれの分点までを底辺とする直角三角形の高さ（分点から斜辺までの垂直距離）を h[1], h[2], ..., h[n-2], h[n-1], h[n] とする。
甲の長さは a = w[n] - w[n-1]，乙の長さは w[n-1] - w[n-2] である。
（分点 w[n] までの）直角三角形全体の面積は S[n] = 底辺*高さ/2 = w[n]*h[n]/2 である。
分点 w[n-1] までの直角三角形の面積はS[n] の (n-1)/n 倍である。 S[n-1] = w[n-1]*h[n-1]/2 = S[n]*(n - 1)/n である。
分点 w[n-2] までの直角三角形の面積はS[n] の (n-2)/n 倍である。 S[n-2] = w[n-2]*h[n-2]/2 = S[n]*(n - )/n である。
この3つの直角三角形に関して以下の連立方程式を解くと，w[n], b[n], w[n-1], b[n-1], w[n-2], b[n-2] が求まる。
甲の長さは w[n] - w[n-1]，乙の長さは w[n-1] - w[n-2] である。
乙の長さは甲の長さの (w[n-1] - w[n-2])/(w[n] - w[n-1]) 倍である。

以下の連立方程式では便宜上 10, 9, 8 を添え字として使っているように見えるが識別のためだけで分割数を n = 10 にしているわけではないことに注意。また，直角三角形の高さは問題を解くに当たっては不要なものである。
このやり方にしたがうと，相似比と面積比の関係などということも考えなくてよい。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms w8::positive, h8::positive,
     w9::positive, h9::positive,
     w10::positive, h10::positive,
     底辺::positive, 高さ::positive, n::positive
S = 底辺*高さ/2
eq1 = w10*h10/2 - S*(n - 0)/n
eq3 = w9*h9/2 - S*(n - 1)/n
eq5 = w8*h8/2 - S*(n - 2)/n
eq2 = h10/w10 - 高さ/底辺
eq4 = h9/w9 - 高さ/底辺
eq6 = h8/w8 - 高さ/底辺;

res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (w10, w9, w8, h10, h9, h8))

   1-element Vector{NTuple{6, Sym}}:
    (底辺, 底辺*sqrt(n - 1)/sqrt(n), 底辺*sqrt(n - 2)/sqrt(n), 高さ, 高さ*sqrt(n - 1)/sqrt(n), 高さ*sqrt(n - 2)/sqrt(n))

甲の長さは以下のようになる。

res[1][1] - res[1][2] |> println  # w10 - w9

   底辺 - 底辺*sqrt(n - 1)/sqrt(n)

乙の長さは以下のようになる。

res[1][2] - res[1][3] |> println  # w9 - w8

   -底辺*sqrt(n - 2)/sqrt(n) + 底辺*sqrt(n - 1)/sqrt(n)

問題が「甲を与えて乙を求める」なので，「乙/甲」の倍率を求める。
簡約化する前は複雑な式に見えるが，簡約化するときれいな形になる。
f = (√(n - 1) - √(n - 2))/(√n - √(n - 1))

f = (res[1][2] - res[1][3]) / (res[1][1] - res[1][2])
f |> simplify |> println

   (-sqrt(n - 2) + sqrt(n - 1))/(sqrt(n) - sqrt(n - 1))

n = 10, 甲の長さ a = 419 のときの乙の長さ 443.00019273604335 は以下のよう求められる。

n = 10
a = 419
a*(√(n - 1) - √(n - 2))/(√n - √(n - 1))

   443.00019273604335

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (底辺, 高さ) = (10, 4)
   n = 10
   plot([0, 底辺, 底辺, 0], [0, 0, 高さ, 0], color=:blue, lw=0.5, showaxis=false)
   delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
   for i = 1:n
       w = 底辺*sqrt(i)/sqrt(n)
       h = w * 高さ/底辺
       segment(w, 0, w, h, :blue)
       point(w, 0, "w$i", :red, :center, delta=-3delta)
       point(w, h, "h$i", :red, :center, :bottom, delta=3delta)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       # vline!([0], color=:black, lw=0.5)
       # hline!([0], color=:black, lw=0.5)
       point(0, 0, "w0", :red, :center, delta=-3delta)
   end
end;

 

算額（その624）

算額（その624）

和算図形問題あれこれ
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html

正方形を 2 本の斜線で区切り，大円 2 個と，小円 2 個を入れる。大円，小円の直径がそれぞれ 7 寸，2 寸のとき，正方形の一辺の長さはいかほどか。

説明のために示した上の図は，大円と中円の直径が 3寸，2寸のときのものである。
正方形の一辺の長さを a, 斜線と左右の辺との交点座標を (0, b), (a, a - b) とおく。
大円の半径と中心座標を r1, (r1, r1)
小円の半径と中心座標を r2, (a - r2, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a::positive, b::positive, r1::positive, r2::positive
(r1, r2) =  (7, 2) .// 2
eq1 = distance(0, b, a, a - b, r1, r1) - r1^2
eq2 = distance(0, b, a, a - b, a - r2, r2) - r2^2
res = solve([eq1, eq2], (a, b))

   2-element Vector{Tuple{Sym, Sym}}:
    (12, 21/2)
    (12, 14)

最初の組のものが適解である。
大円と中円の直径が 7寸，2寸のとき，正方形の一辺の長さは 12, b = 21/2 である。
下図のようになる。上の説明のための図とは大違いである。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (7, 2) .// 2
   (a, b) = (12, 21/2)
   @printf("正方形の一辺の長さ = %g;  b = %g\n", a, b)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:black, lw=0.5, xlims=(-0.6, 13.7), ylims=(-0.6, 12.5))
   circle(r1, r1, r1)
   circle(a - r1, a - r1, r1)
   circle(r2, a - r2, r2, :blue)
   circle(a - r2, r2, r2, :blue)
   segment(0, b, a, a - b)
   segment(a - b, a, b, 0)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(r1, r1, "大円:r1,(r1,r1)", :red, :center, delta=-delta/2)
       point(a - r2, r2, "小円:r2,(a-r2,r2)", :blue, :center, delta=-delta/2)
       point(a, a - b, " (a,a-b)", :black, :left, :vcenter)
       point(0, b, "b ", :black, :right, :vcenter)
       point(0, a, "a ", :black, :right, :vcenter)
       point(a, 0, "a", :black, :center, delta=-delta/2)
   end
end;