014 放散虫：Z^3+0.5画像のフラクタル性(その3)

前記事013の子1画像の中の一部を拡大し、それを孫図と名付ける。


下図は孫図であるが画像構成は子1画像と全く同じ(フラクタル)である。
(この孫図の中の4箇所の部分(A～D)を更に拡大する。)



拡大図(A～D即ち孫1～孫4)は以下のようになる。
(各画像の特徴は各画像に書いてある。)

013 放散虫：Z^3+0.5画像のフラクタル性(その2)

放散虫：Z^3+0.5画像を極座標表示させる。この画像を便宜上、親画像と名付ける。


上の親画像の中の4箇所の部分(A～D)を拡大する。
それぞれの画像を便宜上、A→子1,B→子2,C→子3,D→子4と名付ける。
(注：以後の記事で画像を順次拡大していくため上記のように名づける。)

以下の図から分かるように子1～子4は全く同じ画像構造となっている。

012. 放散虫:Z^3+0.5画像のフラクタル性(その1)

放散虫:Z^3+0.5を拡大していくと1図のようになる。


放散虫：Z^3+0.5の内臓部は2図のようになる。



3図に示すように2図の中の2箇所の部分を拡大する。



-----------------------------------
前記事011で示したように、Z^3+0.5画像は3個の同一画像から構成されている。
それらの3個の同一画像は、更に3個の部分から構成されていることが、3図、4図より分かる。また其れらの画像は入れ子構造となっていることが分かる。
この入れ子構造は無限に続いている。

011. 「放散虫」：Z^n+C 画像について。但しn=正整数、C=実定数 の場合。

Z^n+C 画像(但しn=正整数、C=実定数)画像例を以下に示す。

1図

2図

3図

2図は1図の拡大図(「内臓部」)である。
----------------------------------------------
これらの図の画像作成条件の概略は以下のとおり。
1.N-loop脱出条件：X^2+Y^2>100
2.pset条件：|X|<10 or |Y|<10
3.色:C=No mod 16 (NoはN-loop脱出時のN値)
----------------------------------------------
上図から分かるように『Z^n+C (n：正整数 ,C：実数)の画像は『同形なn個の画像から構成されている。』
この『・・・』の命題が正しければ、このような画像の分析は、n個のうちの1つの画像を調べれば其の調査結果は其の画像全体についての結果になる。　この記事の後で、ちょっとした画像分析をしたいと思っているので、『・・・』が正しいかどうかを調べる。
この程度の問題なら私でも解けそうだ。そこで、昔々の学生時代を偲びつつ証明しよう。
-----------------------------------------
[命題]
『nが正整数、Cが実定数のとき、複素関数：Z^n+Cの“放散虫”の画像は、原点を中心とした扇状にn分割された各領域で、同一な画像から成立している。』

[証明]
複素平面を原点(0,0)を中心として扇状に、同じ大きさにn分割する。第1番目の分割領域内の点(X,Y)を極座標表(R,θ)表示すると、Z=X+iY=R*e^iθとなる。ここで、R=(X^2+Y^2)^0.5,　θ=arctan(Y/X)である。

次に、任意の正整数をm ( < n ) とし、第m番目の分割領域について考える。 Rを一定値にしてθを(2π/n)*m (radian) 回転させると、点(X,Y)は、第m番目の分割領域に移動する。その点を(Xm,Ym)とすると、その点は、Z=Xm+iYm=R*e^i(θ+(2*π/n)*m)となる。

ここで、Z^nを、分割領域1及び分割領域mについて求めてみる。

分割領域1では、Z=R^n*e^i(n*θ)となる。
次に分割領域mでは、Z=(R*e^i(θ+(2*π/n)*m))^n=(R^n)*(e^i((θ+2*π/n)*m*n)=(R^n)*(e^i(n*θ))*e^(i*m*2*π) = (R^n)*e^i(n*θ)(cos(2*m*π)+i*sin(2*m*π)=(R^n)*e^i(n*θ)となり、領域1でのZ^nと一致する。　
(注：cos(2*m*π)=1, sin(2*m*π)=0)

従って、Rを固定値としたとき、領域1と領域mでのZ^n値は全く一致するため、それらの領域での、点(X,Y)と点(Xm,Ym)の挙動は全て一致する。故に、これらの挙動の結果生ずる、任意の条件化下の図形表示は、n分割された領域のそれぞれで、全て一致することになる。

(補足：画像全体の作成手順の概要は、始めRを初期値に固定しθ=0→2πと変化させて計算し、次にRを次の値に固定し、θ=0→2πと変化させて計算する。これを繰り返す)
以上より、複素関数：Z^n+C　の図形は、原点を中心としてn分割された領域で、全く同一の画像から構成されることになる。
(証明終り)

なお、この証明の正しさを確認するため、Z^3の場合について、N-loopの入出力での点(X,Y)の軌跡を調べた。その件については、このブログの後の記事で掲載する予定。

010. cosZと言う名の噴火連山

以下の画像は歪んだ同心円が重なった模様が或る規則性をもって並んでいるユニークな画像である。
これらの画像の同心円模様を連山に見立てると、その連山の各々の頂から黒い噴煙が出ているようにも見える。
各々連山からの噴煙が一つの“かたまり”になっている様子は、いかにも、現実の火山の噴煙を連想させる。
この噴煙のようなモノは、一体、なにを意味しているのだろうか？　(各図の画像作成条件については最後に書いておく。)






---------------------------------------------------------
画像作成条件は以下のとおり。
1. 複素関数:f(Z)=cosZ+0.5
2. 1図の表示画像座標値:横軸(Xi)=-π～+π 縦軸(Yi):-0.75π～+0.75π
3. N-loop脱出条件：Q=tan(X*Y)として、(|Q|>100 or |Q|<0.01)ならば脱出する。
4. Pset条件：N-loop脱出(N=Noとする)後、(|X|<10 or |Y|<10)ならばpsetする。
色:C=No mod 16,C=7→8 とする。
5. Nmax=100 とし、N-loop貫通時は C=0(黒)とする。
---------------------------------------------------------
以下、画像についての説明。

3図から5図から推定できることは以下のことである。

『“噴火点”近くの画像は、その画像の大きさ(スケール)を変えても、画像は変わらない』ということ。

つまり噴火点近くの画像はフラクタルな画像となっていて、おそらく、この噴火点近くの画像は、N-loopのNmaxを、随時、大きくしていけば、永遠に自己相似な画像が続いていくと思われる。

画像の色から分かるように“噴火点”に接近するにつれて、N-loopを脱出するに必要なN値が1ずつ増加している。
(其れは各図の右上に示した色コードから分かる)

従って、『噴火点そのものは、N-loopを脱出するためのN値が無限大となるような、複素平面の特異点である』と言えそうだ。

ともあれ、これらの画像が、単純な計算フルゴリズムから創造されている、純然たる数学上の図形であることを思うと、なにか不思議な感じがする。

数学上の図形というと、三角形だの楕円だのといった、ただただ規則的で単純・無機質・無愛想で、画像としては、すぐ飽きてくるようなツマラナイものと思ってしまいがちだが、いやいや、なかなかどうして、そんなものではないと痛感する。

---------------------------------------------------------
1図の作成のBASIC/98のプログラムを下記しておく。

10 REM cosZと言う名の噴火連山の親
20 REM 横軸(K)：640 dots、縦軸(J)：480 dots
21 CHAIN MERGE "C:BASICPROSUBRCOLOR右上表示.BAS",60,ALL
60 CHAIN MERGE "C:BASICPROSUBRKOSHIKI.BAS",90,ALL
90 CHAIN MERGE "C:BASICPROSUBRER1.BAS",100,ALL
100 ON ERROR GOTO 50000
110 CONSOLE ,,0,1
120 COLOR 0,7,,,2
130 CLS 3
140 GOSUB 10000
150 OPEN "C:BASICRUN画像DATA.DAT" FOR OUTPUT AS #1
160 OPEN "C:BASICRUN親DATA.DAT" FOR OUTPUT AS #2
170 REM 親DATAの設定(随時変更)
180 XS=-P:XE=P:DX=(XE-XS)/640
181 YS=-DX*240:YE=-YS:DY=DX
190 WRITE #2,XS,XE,YS,YE,DX,DY
200 CLOSE #2
240 FOR J=0 TO 480
260 FOR K=0 TO 640
270 X=XS+DX*K
280 Y=YS+DY*J
290 FOR N=0 TO 100
300 X1=X
310 X=FNCOSR(X,Y)+0.5
320 Y=FNCOSI(X1,Y)
330 Q=TAN(X*Y)
340 IF ABS(Q)>100 OR ABS(Q)<0.01 THEN 370 ELSE 350
350 NEXT N
360 C=0 :GOTO 410
370 REM 発散した時点での点(X,Y)のpsetの有無の判定条件
380 IF ABS(X)<10 OR ABS(Y)<10 THEN 390 ELSE 430
390 C=N MOD 16
400 IF C=7 THEN C=8
410 PSET(K,J),C
420 WRITE #1,K,J,C,N
430 NEXT K
440 NEXT J
450 CLOSE #1
451 GOSUB 3000
460 END

009. プログラム実行どきのエラー処理

プログラムを実行ときにエラーが発生したとき其のエラーの内容及びエラー発生行を表示させるプログラムをサブルーチン化しておくと便利である。

以下はBASIC/98 での其のサブルーチン・プログラムである。

50000 *エラー処理
50010 'file name ER1
50020 IF ERR=6 OR ERR=11 THEN 50080 ELSE 50030
50030 PRINT "「overflow」及び「ゼロで除算」以外のエラー"
50040 PRINT "エラー番号=";ERR
50050 PRINT "エラー発生行=";ERL
50060 PRINT "J=";J;"K=";K
50070 STOP
50080 RESUME NEXT

008. 複素関数：f(Z)^g(Z)の実数部と虚数部の計算

f(Z)とg(Z)を任意の複素関数とするとき、f(Z)^g(Z)の実数部と虚数部を求めるプログラムをサブルーチン化しておく。ここで、このサブルーチンの入力値として、f(Z)及びg(Z)の、おのおのの実数部、虚数部は以下のように与えられているとする。

f(Z)の実数部、虚数部を、それぞれ、FZR、FZI とする。
即ち、f(Z)=FZR + i*FZI
g(Z)の実数部、虚数部を、それぞれ、GZR、GZI とする。
即ち、g(Z)=GZR + i*GZI

また、f(Z)は極座標でも表して、f(Z)= =FZR + i*FZI=R*e^iθ　とする。
ここで、R=(FZR^2+FZI^2)^0.5 , θ=arctan(FZI/FZR) である。

上記の条件のもとに、f(Z)^g(Z)の実数部と虚数部を、以下のようにして求める。(以下の式において、掛け算の記号(*)は煩雑さを避けるため適宜省略する)

f(Z)^g(Z)=(R*e^iθ)^( GZR + i*GZI)
=( R^(GZR+i*GZI) )*( e^(iθ(GZR+iGZI) )
=( R^GZR)* ( e^(-θ*GZI) ) * (R^i*GZI)*(e^iθGZR)
ここで、ZF1= (R^GZR)* ( e^(-θ*GZI) とおけば、
f(Z)^g(Z)=ZF1* (R^i*GZI)*(e^iθGZR)
=ZF1*( e^(logR))^(iGZI) ) * (e^iθGZR) (ここで、logの底はeとする)
　　　　=ZF1*e^i*(logR*GZI+θ*GZR)
ここで、ZF2=logR*GZI+θ*GZR とおけば、
f(Z)^g(Z)=ZF1*e^i*ZF2
=ZFI*(cosZF2+i*sinZF2)
となり、f(Z)^g(Z)の実数部=ZF1*cosZF2
f(Z)^g(Z)の虚数部=ZF1*sinZF2
となる。ここで、ZF1= (R^GZR)* ( e^(-θ*GZI)
　　　　　　　　ZF2=logR*GZI+θ*GZR　
である。従って、f(Z)^g(Z)の実数部と虚数部を求めるプログラムをサブルーチン・プロクグラムは以下のようにすればよい。

30000 REM f(Z)^g(Z)の計算：file name FGZ
30010 IF R=0 THEN 30060
30020 ZF1=(R^GZR)*EXP(-TH*GZI)
30030 ZF2=TH*GZR+LOG(R)*GZI
30040 FZGZR=ZF1*COS(ZF2)
30050 FZGZI=ZF1*SIN(ZF2)
30060 RETURN

006. 複素関数:Z^f(Z)の実数部と虚数部の計算

Zを複素平面上の点とし、f(Z)を任意の複素関数とするとき、複素関数：Z^f(Z)の実数部と虚数部を求める計算プログラムをサブルーチン化ておく。

そのために、Z^f(Z)の実数部と虚数部を以下のようにして求める。

Z=X+iY=R*e^iθとし，ここで、R=(X^2+Y^2)^0.5 ,θ=arctan(Y/X)から、Rとθは、このサブルーチンの入力値とする。また、任意のf(Z)の実数部(これをREFとする)と虚数部(これをIMFとする)も既に与えられているとする。

即ち、f(Z)=FZR+i*FZI とする。 (ここで、FZR , FZI は既知の実数とする)

(以下の計算式において掛け算の記号(*)は煩雑さを避けるため適宜省略する。)

Z^f(Z)=( R*e^iθ)^( FZR+i*FZI)=( (R*e^iθ)^FZR)*( (R*e^iθ)^iFZI )
=(R^FZR)*(e^(iθ*FZR))*(R^iFZI)*e^(-θ*FZI)
=(R^FZR)*e^(-θ*FZI)*e^(iθ*FZR)*R^(i*FZI)
　　ここで、ZF1=(R^FZR)*e^(-θ*FZI) とおくと、

Z^f(Z)=ZF1* ( e^(iθ*FZR)*R^(i*FZI) ) ・・・・・(1)
　 ここで、R=e^logR 　(但し、logの底はeとする)　だから
　　R^(i*FZI)=(e^logR)^(i*FZI)=e^(i*logR*FZI)
従って、(1)より、
Z^f(Z)=ZF1*e^i(θ*FZR+logR*FZI)
ここで、ZF2=θ*FZR+logR*FZI とおくと、
Z^f(Z)=ZF1*e^(*ZF2)=ZF1*(cosZF2+i*sinZF2)
=ZF1*cosZF2 + i*(ZF1*sinZF2)
となるから、
Z^f(Z)の実数部= ZF1*cosZF2
Z^f(Z)の虚数部= ZF1*sinZF2
( 但し、ZF1=(R^FZR)*e^(-θ*FZI) , ZF2=θ*FZR+logR*FZI )

となり、Z^f(Z)の実数部と虚数部が求まった。
従って、Z^f(Z)の実数部と虚数部を、それぞれ、ZFZR,ZFZIとすれば、求めるサブルーチン・プログラムは下記のようになる。

20000 REM Z^(f(z)の計算：file name ZFZ
20010 IF R=0 THEN 20060
20020 ZF1=(R^FZR)*EXP(-TH*FZI)
20030 ZF2=TH*FZR+LOG(R)*FZI
20040 ZFZR=ZF1*COS(ZF2)
20050 ZFZI=ZF1*SIN(ZF2)
20060 RETURN

005. 複素関数:Z^Zの実数部と虚数部の計算

複素平面上の点Zが与えられていたとき、複素関数：Z^Zの実数部と虚数部の計算をサブルーチン化しておく。　ここで、このサブルーチンを実行するときは、点ZのX,Y,R及びθ(プログラムでの変数名：TH)は、与えられているものとする。また、自然対数eの底(プログラムでの変数名：EE)も与えられているものとする。

X及びYから、R及びθは、R=(X^2+Y^2)^0.5 , θ=arctan(Y/X) より求める。(注：θ=arctan(Y/X) は、あらかじめ、サブルーチン ARCTAN3A で求めておく。)

複素関数：Z^Zの実数部と虚数部の計算方法を以下に示す。
(これも私が数学の公式集を参考にして計算したものであるから誤りがあるかも知れないから御注意！！　：　下式で掛け算の記号(*)は適宜付けたり省力したりしている。下式はゴチャゴチャしているが、やっていることは単純なこと。こういうところが数式というものの欠点の一つだと思う。)

Z^Z={R*e^(iθ)}^(X+iY)={R^(X+iY)}*[{e^(iθ)}^{(X+iY)}]
=[(R^X)*{R^(iY)}]*[e^{iθ*(X+iY)}
=[(R^X)*e^(-θY)]*[(R^iY)*(e^iθX)]・・・(1)

ここで、上式を分かりやすくするために、
A=(R^X)*e^(-θY)
とおくと、
Z^Z=A*[(R^iY)*(e^iθX)]・・・(2)

ここで、e^x=R として、x を求める。logの底をeとすると、
logR=log(e^x)=x*log e=x

従って、R=e^x=e^logR　だから、(1)式の第2項に、このRを代入すると、
(1)式の第2項=[(R^iY)*(e^iθX)]={(e^logR)^iY}*{(e^iθX)}
={e^i(YlogR)} *{(e^iθX)}
=e^i(YlogR+θX)・・・(3)

ここで、上式を分かりやすくするために、
B=(YlogR+θX)
とおくと、
(1)式の第2項=(3)式=e^iB=cosB+isinB
となるから、(1)式、即ち、Z^Z は、
Z^Z=A*(3)式=A*( cosB+isinB)=AcosB +i(AsinB)
となる。従って、
Z^Zの実数部= AcosB
Z^Zの虚数部= AsinB
となる。ここで、
A=(R^X)*e^(-θY) 　, B=(YlogR+θX)

以上より、Z^Zの実数部と虚数部を計算するサブルーチン・プログラムは、下記のようにします。下記のプログラムの行9010,9020,9040,9060及び9070は、使用しているBASICの制約によるもので、本来は不要です。

9000 REM Z^ZのRe.ZとIm.Zの計算
9002 REM ZのX,Y,R,θ(TH)は与えられているものとする。
9004 REM 自然対数の底e：EE=2.718281も与えられているものとする。
9010 IF TH*Y<-709 THEN TH*Y=-709 :GOTO 9030
9020 IF TH*Y>709 THEN TH*Y=709
9030 A1=(R^X)*EE^(-TH*Y)
9040 IF R=0 THEN R=1E^-100
9050 B=Y*LOG(R)+TH*X
9060 IF B>1.0E+9 THEN B=1.0E+9 :GOTO 9080
9070 IF B<-1.0E+9 THEN B=-1.0E+9
9080 ZZR=A1*COS(B)
9090 ZZI=A1*SIN(B)
9100 RETURN

上記のプログラムにおいて、Z^Zの実数部値をZZRとおき、Z^Zの虚数部値をZZIとした、それらをメイン・プログラムへ、RETURNすればよい。

004. 算術関数ATNの計算方法

BASIC/98での、arctan(Y/X)の算術関数ATN(X/Y)の演算結果は、
-π/2～π/2の値となります。従って、上図の図１の、第一及び第四象限では、算術関数ATN(X/Y)は、そのままの値で問題はない。問題となるのは、第二及び第三象限の場合である。

第二及び第三象限の場合でのθ=arctan(Y/X)の計算方法は、いくつか考えられるが、其のいくつかの方法を試みた結果、私は、現在、上図方法で計算している。

この方法が、現在のところ、全象限での画像の連続性は最も良い。
これは経験上のことで未だ理屈として正しいのかどうか確信はない。
もっと理屈にかなったθ=arctan(Y/X)の計算方法が有るかも知れない。
--------------------------------------------------
私は、θ=arctan(Y/X)の計算は下記のようなプログラムでサブルーチン化している。

5000 REM θの計算:file name ARCTAN3A
5010 IF X=0 THEN 5020 ELSE 5050
5020 IF Y=0 THEN TH=0 :GOTO 5090
5030 IF Y>0 THEN TH=P/2 ELSE TH=-P/2
5040 GOTO 5090
5050 AA=Y/X
5060 IF X>0 THEN TH=ATN(AA) :GOTO 5090
5070 IF X<0 AND Y>0 THEN TH=ATN(AA)+P :GOTO 5090
5080 IF X<0 AND Y<0 THEN TH=ATN(AA)-P
5090 RETURN

003 複素関数の実数部と虚数部について

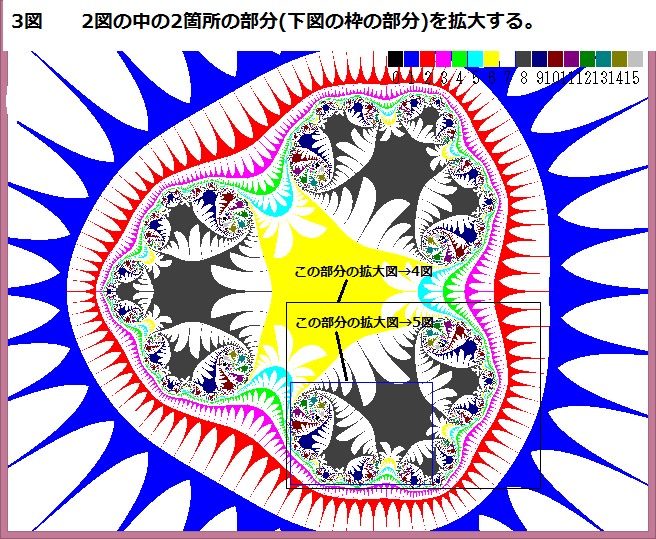
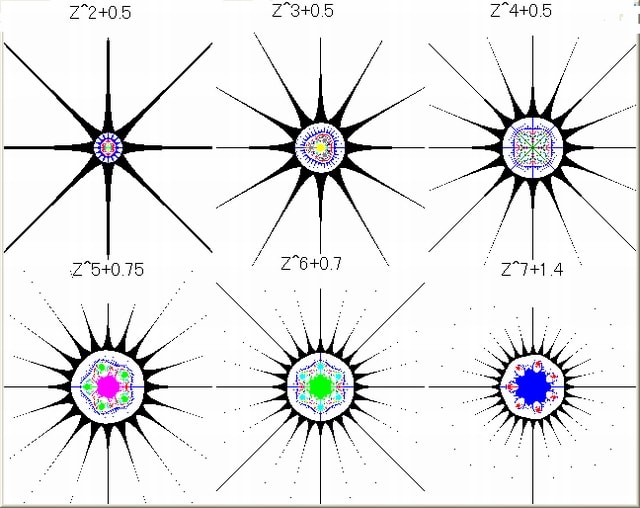
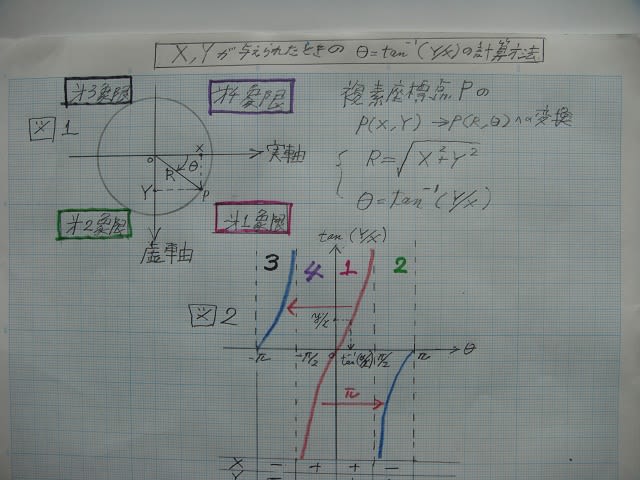
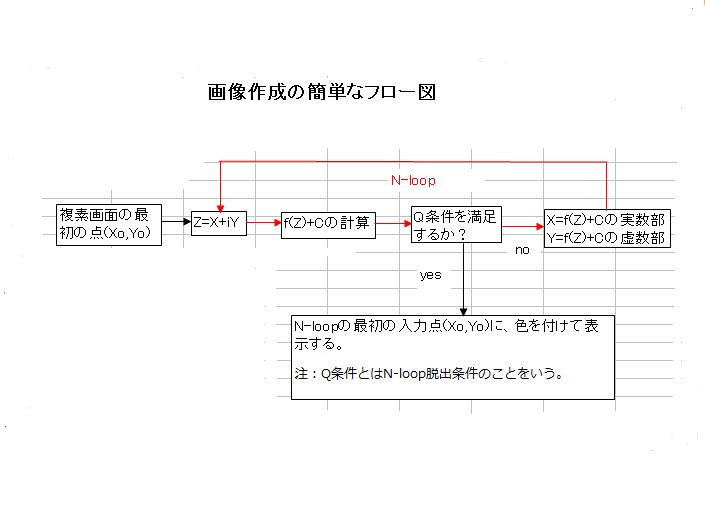
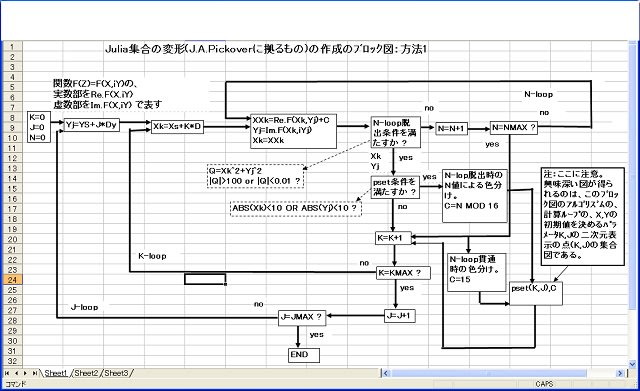
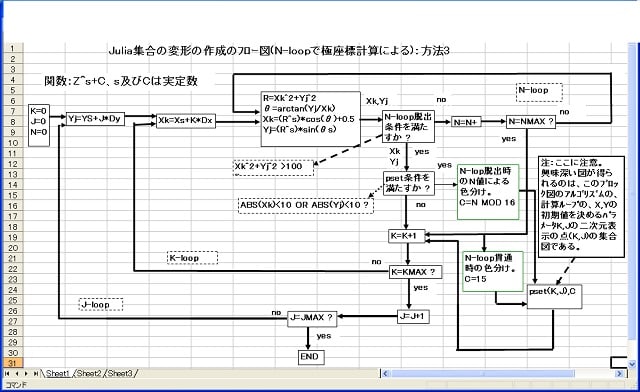
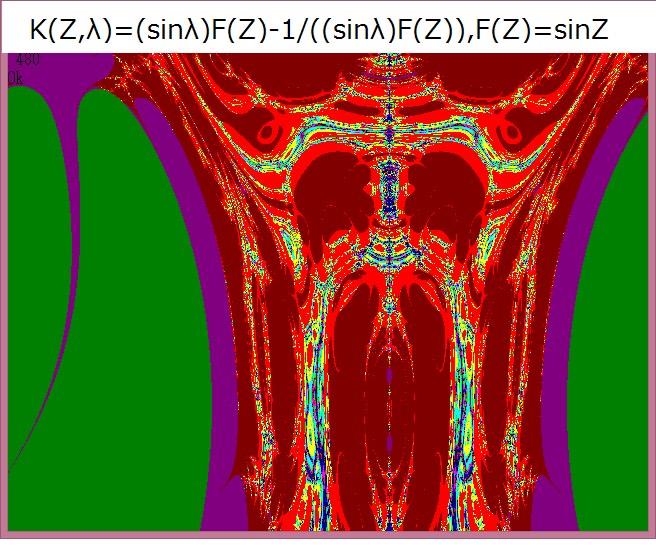
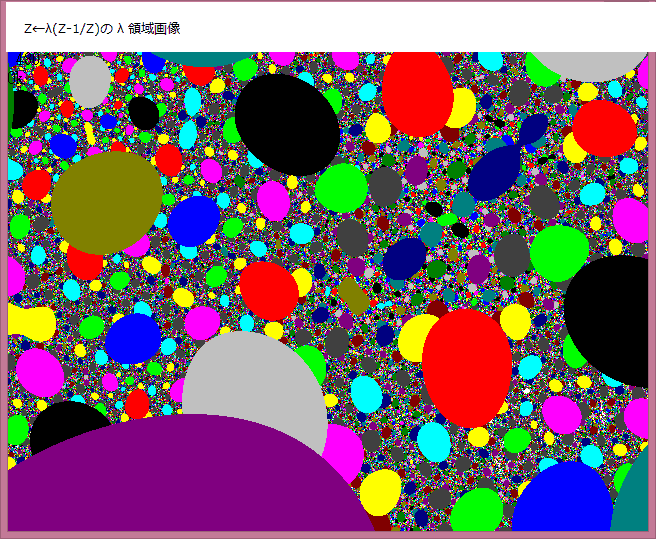
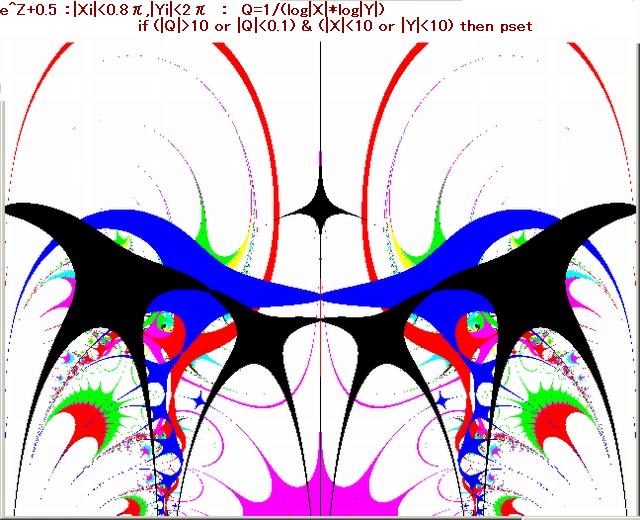
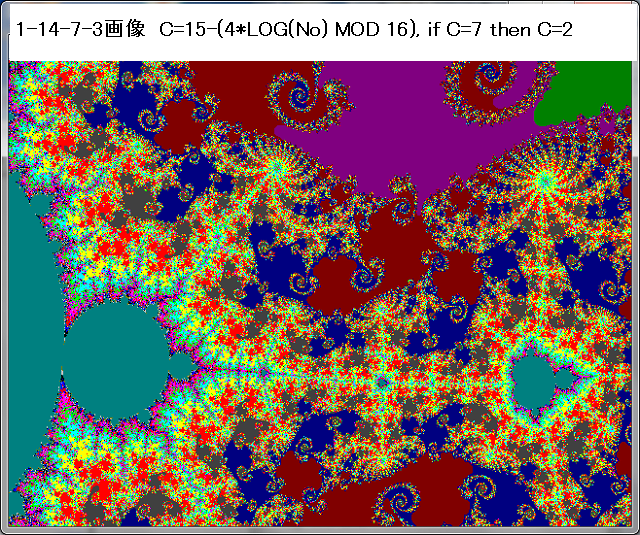
以下のリストのように、複素関数の実数部と虚数部はサブルーチン化しておき、本体プログラムより必要に応じて DEF FN コマンドで呼び出している。関数は随時追加している。
-------------------------------------------------------
10000 REM KOSHIKI FILE NAME KOSHIKI ,Ver.4
10010 EE=2.718281# :P=3.141592#
10020 DEF FNSINH(X)=.5#*(EE^X-EE^(-X))
10030 DEF FNCOSH(X)=.5#*(EE^X+EE^(-X))
10040 REM Z^n
10050 DEF FNR2(X,Y)=X^2-Y^2
10060 DEF FNI2(X,Y)=2*X*Y
10070 DEF FNR3(X,Y)=X*(X^2-3*Y^2)
10080 DEF FNI3(X,Y)=Y*(3*X^2-Y^2)
10090 DEF FNR4(X,Y)=FNR2(X,Y)^2-FNI2(X,Y)^2
10100 DEF FNI4(X,Y)=2*FNR2(X,Y)*FNI2(X,Y)
10110 DEF FNR5(X,Y)=FNR2(X,Y)*FNR3(X,Y)-FNI2(X,Y)*FNI3(X,Y)
10120 DEF FNI5(X,Y)=FNR2(X,Y)*FNI3(X,Y)+FNI2(X,Y)*FNR3(X,Y)
10130 DEF FNR6(X,Y)=FNR3(X,Y)^2-FNI3(X,Y)^2
10140 DEF FNI6(X,Y)=2*FNR3(X,Y)*FNI3(X,Y)
10150 DEF FNR7(X,Y)=X*FNR6(X,Y)-Y*FNI6(X,Y)
10160 DEF FNI7(X,Y)=Y*FNR6(X,Y)+X*FNI6(X,Y)
10170 DEF FNR8(X,Y)=FNR6(X,Y)*FNR2(X,Y)-FNI6(X,Y)*FNI2(X,Y)
10180 DEF FNI8(X,Y)=FNR6(X,Y)*FNI2(X,Y)+FNI6(X,Y)*FNR2(X,Y)
10190 DEF FNR9(X,Y)=FNR6(X,Y)*FNR3(X,Y)-FNI6(X,Y)*FNI3(X,Y)
10200 DEF FNI9(X,Y)=FNR6(X,Y)*FNI3(X,Y)+FNI6(X,Y)*FNR3(X,Y)
10210 DEF FNR10(X,Y)=FNR6(X,Y)*FNR4(X,Y)-FNI6(X,Y)*FNI4(X,Y)
10220 DEF FNI10(X,Y)=FNR6(X,Y)*FNI4(X,Y)+FNI6(X,Y)*FNR4(X,Y)
10222 DEF FNR11(X,Y)=FNR6(X,Y)*FNR5(X,Y)-FNI6(X,Y)*FNI5(X,Y)
10224 DEF FNI11(X,Y)=FNI6(X,Y)*FNR5(X,Y)+FNR6(X,Y)*FNI5(X,Y)
10226 DEF FNR12(X,Y)=(FNR6(X,Y))^2-(FNI6(X,Y)^2)
10228 DEF FNI12(X,Y)=2*FNR6(X,Y)*FNI6(X,Y)
10230 DEF FNR13(X,Y)=FNR6(X,Y)*FNR7(X,Y)-FNI6(X,Y)*FNI7(X,Y)
10232 DEF FNI13(X,Y)=FNI6(X,Y)*FNR7(X,Y)+FNR6(X,Y)*FNI7(X,Y)
10238 REM Sin Z
10240 DEF FNSINR(X,Y)=.5#*SIN(X)*(EE^Y+EE^(-Y))
10250 DEF FNSINI(X,Y)=.5#*COS(X)*(EE^Y-EE^(-Y))
10260 REM COS Z
10270 DEF FNCOSR(X,Y)=.5#*COS(X)*(EE^Y+EE^(-Y))
10280 DEF FNCOSI(X,Y)=-.5#*SIN(X)*(EE^Y-EE^(-Y))
10282 REM TAN Z
10284 DEF FNTANR(X,Y)=FNSINR(X,Y)*FNCOSR(X,Y)-FNSINI(X,Y)*FNCOSI(X,Y)/((FNCOSR(X,Y))^2+(FNCOSI(X,Y))^2)
10286 DEF FNTANI(X,Y)=FNSINR(X,Y)*FNCOSI(X,Y)+FNCOSR(X,Y)*FNSINI(X,Y)/((FNCOSR(X,Y))^2+(FNCOSI(X,Y))^2)
10290 REM e^Z
10300 DEF FNEZR(X,Y)=COS(Y)*EE^X
10310 DEF FNEZI(X,Y)=SIN(Y)*EE^X
10320 REM Sinh Z
10330 DEF FNSINHR(X,Y)=.5#*COS(Y)*(EE^X-EE^(-X))
10340 DEF FNSINHI(X,Y)=.5#*SIN(Y)*(EE^X+EE^(-X))
10350 REM Cosh Z
10360 DEF FNCOSHR(X,Y)=.5#*COS(Y)*(EE^X+EE^(-X))
10370 DEF FNCOSHI(X,Y)=.5#*SIN(Y)*(EE^X-EE^(-X))
10380 REM Sin(Sin Z)
10390 DEF FNSINSINR(X,Y)=SIN(FNSINR(X,Y))*FNCOSH(FNSINI(X,Y))
10400 DEF FNSINSINI(X,Y)=COS(FNSINR(X,Y))*FNSINH(FNSINI(X,Y))
10410 REM Cos(Sin Z)
10420 DEF FNCOSSINR(X,Y)=COS(FNSINR(X,Y))*FNCOSH(FNSINI(X,Y))
10430 DEF FNCOSSINI(X,Y)=-SIN(FNSINR(X,Y))*FNSINH(FNSINI(X,Y))
10440 REM e^(Z^2)
10450 DEF FNEZR2(X,Y)=(EE^(FNR2(X,Y)))*COS(FNI2(X,Y))
10460 DEF FNEZI2(X,Y)=(EE^(FNR2(X,Y)))*SIN(FNI2(X,Y))
10470 REM e^(Z^3)
10480 DEF FNEZR3(X,Y)=(EE^(FNR3(X,Y)))*COS(FNI3(X,Y))
10490 DEF FNEZI3(X,Y)=(EE^(FNR3(X,Y)))*SIN(FNI3(X,Y))
10500 REM e^(Z^4)
10510 DEF FNEZR4(X,Y)=(EE^(FNR4(X,Y)))*COS(FNI4(X,Y))
10520 DEF FNEZI4(X,Y)=(EE^(FNR4(X,Y)))*SIN(FNI4(X,Y))
10530 REM e^(Z^5)
10540 DEF FNEZR5(X,Y)=(EE^(FNR5(X,Y)))*COS(FNI5(X,Y))
10550 DEF FNEZI5(X,Y)=(EE^(FNR5(X,Y)))*SIN(FNI5(X,Y))
10560 REM e^(Z^6)
10570 DEF FNEZR6(X,Y)=(EE^(FNR6(X,Y)))*COS(FNI6(X,Y))
10580 DEF FNEZI6(X,Y)=(EE^(FNR6(X,Y)))*SIN(FNI6(X,Y))
10590 REM e^(Z^7)
10600 DEF FNEZR7(X,Y)=(EE^(FNR7(X,Y)))*COS(FNI7(X,Y))
10610 DEF FNEZI7(X,Y)=(EE^(FNR7(X,Y)))*SIN(FNI7(X,Y))
10620 REM e^(Z^8)
10630 DEF FNEZR8(X,Y)=(EE^(FNR8(X,Y)))*COS(FNI8(X,Y))
10640 DEF FNEZI8(X,Y)=(EE^(FNR8(X,Y)))*SIN(FNI8(X,Y))
10650 REM e^(Z^9)
10660 DEF FNEZR9(X,Y)=(EE^(FNR9(X,Y)))*COS(FNI9(X,Y))
10670 DEF FNEZI9(X,Y)=(EE^(FNR9(X,Y)))*SIN(FNI9(X,Y))
10680 REM e^(Z^10)
10690 DEF FNEZR10(X,Y)=(EE^(FNR10(X,Y)))*COS(FNI10(X,Y))
10700 DEF FNEZI10(X,Y)=(EE^(FNR10(X,Y)))*SIN(FNI10(X,Y))
10710 REM e^(SIN Z)
10720 DEF FNEZSINR(X,Y)=(EE^(FNSINR(X,Y)))*COS(FNSINI(X,Y))
10730 DEF FNEZSINI(X,Y)=(EE^(FNSINR(X,Y)))*SIN(FNSINI(X,Y))
10740 REM e^(SINH Z)
10750 DEF FNEZSINHR(X,Y)=EE^(FNSINHR(X,Y))*COS(FNSINHI(X,Y))
10760 DEF FNEZSINHI(X,Y)=EE^(FNSINHR(X,Y))*SIN(FNSINHI(X,Y))
10780 REM e^(COS Z)
10790 DEF FNEZCOSR(X,Y)=(EE^(FNCOSR(X,Y)))*COS(FNCOSI(X,Y))
10800 DEF FNEZCOSI(X,Y)=(EE^(FNCOSR(X,Y)))*SIN(FNCOSI(X,Y))
10810 REM e^(COSH Z)
10820 DEF FNEZCOSHR(X,Y)=EE^(FNCOSHR(X,Y))*COS(FNCOSHI(X,Y))
10830 DEF FNEZCOSHI(X,Y)=EE^(FNCOSHR(X,Y))*SIN(FNCOSHI(X,Y))
10840 RETURN----------------------------------------

002. 画像作成のプログラムと色及びNoのlog化の概略説明

（Ａ)・ジュリィア集合変形画像とマンデルブロー画像の以下のように此のブログでは定義する。

・ジュリィア集合変形画像の定義

『ある任意の複素関数をf(Z)+Cとします。Cは実数でも虚数でも構いません。
ある複素画面領域の点(Z=X+iY)において、01.図～04.図の計算手順を満足したとき、その点に色を付けて、その点Zを表示する。この手順を複素画面領域全てについて行い画像を完成させる。』

これとは少し異なる手順の画像作成条件を考える。便宜上、そのような画像をマンデルブロ画像と名づける。この画像作成方法は以下のとおりとする。

・マンデルブロー画像の定義

『ある任意の複素関数をf(Z)+Cとします。Cは複素数でRe.C=CX,Im.C=CYとする。
ある複素画面領域の点(CX,CY)において、Z=X+iYとしてf(Z)+Cを上のフロー図のように計算を行います。この計算手順を満足したとき点(CX,CY)に色をつけて表示する。
この手順をCの複素画面領域全てについて行い画像を完成させる。』

注：複素関数をf(Z)+Cとしたとき、『ジュリィア集合変形画像』の複素画面表示はZ=X+iYで点(X,Y)の集合であり、『マンデルブロー画像は点(CX,CY)の集合』である。

----------------------------------------------------------------------

（Ｂ）ジュリィア集合変形画像の作成手順のプログラム・概略フロー図を以下に示す。



なお極座標を用いた画像作成については下記の2.及び3.を適宜、使用しているが詳細説明は割愛する。

以下此のブログでのジュリィア集合変形画像作成の詳細なプログラム・フロー図を示しておく。

1.方法1：ジュリィア集合変形画像作成のフロー図。



2.方法2：ジュリィア集合変形画像作成のフロー図。(極座標によるもの：1)



3.方法3：ジュリィア集合変形画像作成のフロー図。(極座標によるもの：2)



--------------------------------------------------------------------

（Ｃ）マンデルブロー集合変形画像の作成手順のプログラム・概略フロー図を以下に示す。



---------------------------------------------------

（Ｄ）画像の色の説明を以下に示す。







---------------------------------------------------
（Ｅ）N-loop脱出時のNoのLOG化について。

4 N-loop脱出時のNoのLOG化について。

以下においてLOGの底はeである。
BASIC/98において使用できるのは最大16色であり、その色は、O～15の中の整数(Cとする)
で指定される。その具体的な配色は上記（Ｄ）項のように決められている。

従って、このブログでは、N-loop脱出時のNをNoとしたとき、Noを色Cで表現する場合、
No＞16では、C=No MOD 16として、16進法で゛色を決めている。

マンデルブロ画像のように画像構造が細密な個所では、Noが複雑に変化し、その結果、そのような個所で色が複雑に変化して分かりにくくなる。

そのような場合の画像構造を、より分かりやすくするために、NoをLOG化することが考えられる。　以下、NoをLOG化した場合の検討である。

***

LOG(No)が、1 だけ変化変化した場合(即ち、色Cが次の色に変化した場合)、
Noは、どれだけ変化するのだろうか?

いま、Noの値としてNa,Nbを考え、LOG(Nb)-LOG(Na)=1　とする。
従って、LOG(Nb/Na)=1 故に、Nb/Na=e=2.72 故に　Nb=2.72Na　となる。

従って、LOG(No)が、1 だけ変化した場合、Noは 2.72 変化していることになる。

逆に言うと、Noが2.72倍変化したとき、色Cが次の色に変わり、画像の色変化が緩和され、
色のよるが画像構造が容易になる(但し、それだけ色による構造分析は粗くなる)

BASIC/98の色配色(整数:Cに対する色の配色)は、画像構造の解析において適当とは言えず、配色を移動させたほうがよい場合がある。

その場合に、Noに適当な係数を掛け配色を移動させる。

例えば、その係数を10^6とすると、
LOG(10^6*No)=LOG(10^6)+LOG(No)=6*LOG(10)+LOG(No)=13.8+LOG(No)

となり、13.8→13 or 12 だけ配色が移動する。

注：配色移動は、C=(適当な整数+LOG(No) としてもよいが、Noに直接、適当な係数を掛けたほうが精度が上がるから上記の方法にした。

***

{ 要約と要点 }

『複素平面上の画像において、このブログでは、Noを色Cで表現している。
マンデルブロ画像のように、画像のある個所においては画像が細密になり(即ち、Noの変化が
細密になり)、Noの表現である色Cの区別が識別しにくくなる。

そのために、NoをLOG(No)で表現する。
そうすることによって、N=2.72*Noになったとき次の色に変わる。

例：No=2(C=2:赤)のとき、N=2.72*2=5.44→5になったとき、次の色:C=3(紫)に変わる。
この場合は、N=2～4はC=2(赤)として単一表現され画像の色の変化が単純化される。

また、単純化されるNの値の数はNに依存し、N→大程大きくなる。
最大となるのは、No MOD 16=15 のときで、15*2.72=40.8→40 となりNoの変化が40でも同一色で表示され、画像解析が容易となる。

この色の単純化(グループ化)は、実際には、Noの係数(例:10^6)を含めてのLOG化と色の16進法化で行われるから、これ自体が複雑な操作であるが、LOG(No)化によって画像の色による解析が容易になることは確かである。但し、その分、解析は粗くはなる。

001. 初めに & 画像例

拝啓。

これからパソコンを使って画像の作成遊びを気が向くままボチボチとしていきたいと思います。
　
どんな画像遊びかというと、その“たね本”がありまして其れは『コンピューター・カオス・フラクタル－見えない世界のグラフィクス－』(クリフォード・Ａ・ピックオーバー著、白揚社)です。

この本では、いわゆるマンデルブロー図形や、その他の種々の奇妙で不思議な図形が、とても分かりやすく、たくさん紹介されていて其れら図形・画像の作り方のプログラムも掲載されています。　この本の「はじめに」には、この本の意図・特徴がよく表現されています。少し長いですが引用してみましょう。

---------------------------------------------------------------
『私はときどき自分を釣り師になぞらえてみる。コンピューター・プログラムとアイデアは釣り針であり、リールである。コンピューターで描きあげた絵はトロフィーであり、うまいご馳走である。釣り師には、何が釣れるかがいつもわかっているわけではない。しかし、どこがよく釣れるか、どの流れに魚がたまっているか、などについての知識はもっているだろう。しばしばびっくりするほどの大物が釣れるが、これこそまさに釣りの醍醐味である。しかし保証はない。そのかわり予期しない楽しみもある。読者もぜひ未知の釣り場で実際に糸を垂れてほしい。できれば釣りあげた獲物を観賞し更に其れを解剖し内部の構造を調べてほしい。』
--------------------------------------------------------------

私も釣り竿を持って複素平面という名の池へ行ってノンビリと釣り糸を垂れよう、というわけです。　

釣り竿や釣り針は、多くのみなさんも、昔(と言っても、かれこれ２０年ほど前ですかねぇ)、使っていたインタプリターＢＡＳＩＣ言語のＢＡＳＩＣ／９８(電脳組)を使います。

このテの画像遊びには適しない言語でしょうが、私は昔、職場で此れを学ばされまして退職後、此の遊びに使ってやれと思いたった次第です。それなりに楽しめます。

もちろん、画像の面白さは主観的なものであり他の人にはツマラナイものかも知れません。

なお此のブログではジュリィア変形集合画像とマンデルブロー集合画像を主として作成しています。それらの画像の説明についてはカテゴリー『画像作成の説明』で説明しています。

ではではーーーー

追啓：このブログでは複素関数を使用していますが其の使い方( 主として複素関数の実数部と虚数部の求め方 )に、数学上の間違いがあるかも知れません。その点、承知おき願います。



------------------------------------------------
以下は此のブログでの画像例です。