PCが描く奇妙な画像集(数学的万華鏡と生物形態等の世界)

・インタープリタBASICによるフラクタルとカオスの奇妙な画集。

028 e^sinZ 画像

2014-06-19 13:41:21 | ジュリィア集合の変形：e^f(Z)+C
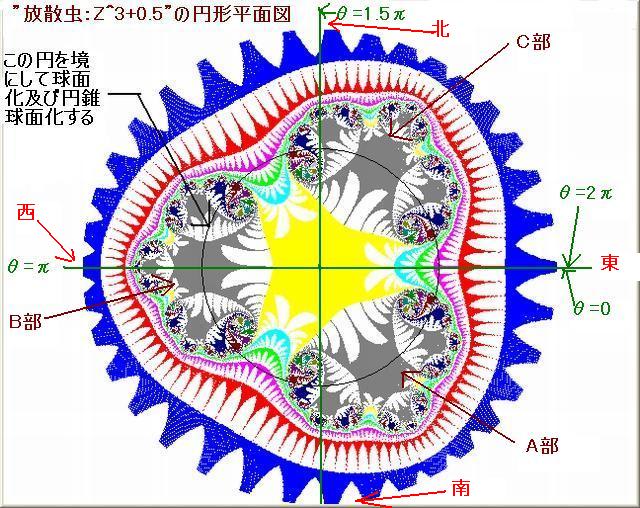
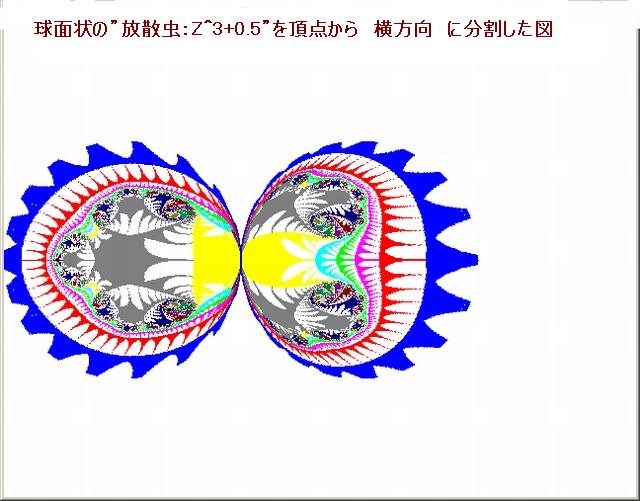
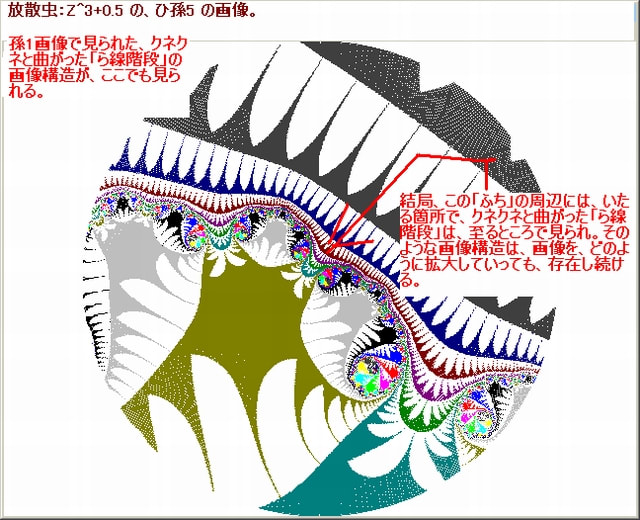
下図は e^sinZ 画像と其の画像の中の 8 箇所の部分の拡大画像である。
画像作成条件は最後に書いておく。




-----------------------------------------------------------








-----------------------------------
画像作成条件：
・『複素関数は e^sin Z +0.5』
・『N-loopを脱出するのは、Q=tanX*tanYとしたとき、もし、( |Q|>100 or Q|<0.01 ) ならば 脱出する』
・『N-loop脱出後、もし、(|X|<10 or |Y|<10)ならばpsetする』
・最初の画像のN-loop の入力値(Xi,Yi)が 0<=Xi<=3π, |Yi|<=1.1π

025 放散虫：sinZ+Z^2+0.5画像のフラクタル性

2014-06-19 07:49:50 | ジュリィア集合の変形：f(Z)+g(Z)+C
1.図　放散虫：sinZ+Z^2+0.5画像の中の3 箇所を拡大する




2.図　1図の 1 の拡大画像




3.図　1図の 2 の拡大画像




4.図　1図の 3 の拡大画像




***
3.図について。

この画像は 3 段の同形の重層構造となっている。

特に興味深いのは此の画像の右側の上下の目玉のような部分には此の画像の中央部の画像の歪んだコピーが居る。そして此の画像にはＷ型の「つばめ」も居る。かなり複雑なフラクタル構造画像である。

021 放散虫：Z^3+0.5画像の変形化2 (球面化1)

2014-06-18 09:17:11 | ジュリィア集合の変形：Z^s+C
1.図に示す円形型の放散虫：Z^3+0.5画像を球面化し、その画像を東西南北から眺めたら、どんな画像になるだろうか？　それらの画像を2.～5.図に示す。

1.図


2.図　球面型の放散虫を東側から見た画像


3.図　球面型の放散虫を南側から見た画像


4.図　球面型の放散虫を西側から見た画像


5.図　球面型の放散虫を北側から見た画像


***
また此の球面化した画像を2分割したら、どんな画像になるだろうか？
それらの画像を数に示す。




019 放散虫：Z^3+0.5画像の規則性と不規則性の混在について(その2)

2014-06-18 07:22:19 | ジュリィア集合の変形：Z^s+C
前回の記事018では、N-loop脱出時のX,Yを別々に調べてきたか゛今回は点(X,Y)の挙動を調べてみる。

補足：以下の図1の画像の作成プログラムは記事002の方法2である。複素平面上の点(R,θ)が画像の表示条件を満足したとき、その点(R,θ)を所定の色で表示している。N-loopの脱出時の(X,Y)を表示しているのでない。ここらへんが混乱しやすいの要注意。

1.図


調べる箇所は、「内臓」部の一部であるR=0.65のところでRを固定し、θを20度から30度に変化させて、その場合のN-loop脱出時の点(X,Y)の軌跡を調べる。その結果が2.図である。

2.図


上図から分かるように、「内臓」部では、N-loopの入力点(R,θ)に対応した、N-loopの出力点(X,Y)の軌跡が複雑に飛び回るために、その結果として、放散虫：Z^3+0.5の「内臓」部の画像も複雑になっている。
次に、「触手」部であるR=1.3のところでRを固定し、θを0度から60度に変化させた場合の、N-loop脱出時の点(X,Y)の軌跡を3.図に示す。

3.図


上図から分かるように、「触手」部では、N-loopの入力点(R,θ)に対応した、N-loopの出力点(X,Y)の軌跡は単純な変化であるため、その結果として、放散虫：Z^3+0.5の“触手”部の画像も単純になっている。

018 放散虫：Z^3+0.5画像の規則性と不規則性の混在について(その1)

2014-06-17 09:34:04 | ジュリィア集合の変形：Z^s+C
放散虫：Z^3+0.5の画像構造を少し定量的的に調べてみる。
(補足：この画像の作成プログラムは記事002の方法2である。)

記事011で示したように、Z^n+C 画像(但し、n=正整数,C=実定数)は、n 個の全く同一な画像から構成される。従って此の画像を解析する場合、n 個の中の 1 個の部分のみ解析すれば画像全体の構造が分かる。

1.図はZ^3+0.5画像を極座標表示した場合の、θ=0～(2/3)/π までの 1/3 部分である。この部分のみ解析すれば其の結果は全体画像にも言えることになる。
(注：画像の色が今まで記事と異なるのは、N-loop を1→Nmax したためで・・・今迄の画像は 0→Nmaxとしていた・・・あって本質的には今迄画像と同一である。)

1.図



2.図

2.図はRを0→9 変化させたときの、N-loop脱出時のXとYの変化を示した図である。

(補足：1.画像は、複素平面上の点(R,θ)が画像の表示条件を満足したとき、その点(R,θ)を所定の色で表示している。N-loopの脱出後の(X,Y)を表示しているのでない。ここらへんが混乱しやすいの要注意。)

2.図の色は、1.図の色と対応させている。この図で分かる大事なポイントの一つは、このXとYの画像が規則的な箇所と不規則的な箇所が混ざっている、ということである。

1.図と見比べてみると分かることだが、規則的な箇所は“放散虫：Z^3+0.5”の「触手」部分であり、不規則的な箇所は「内臓」部分だ。

放散虫：Z^3+0.5の「内臓」部分の画像の複雑さは、XとYの変化の不規則性に依っている。そして放散虫：Z^3+0.5”の「触手」部分の画像の単純さは、XとYの変化の規則性に依っているのだ。R=0～1部分のみを横軸に拡大してみた図が次の3.図である。

3.図

上図は、1.図のRを0→1まで (つまりに「内臓」部での) N-loop脱出時のXとYの変化を示した図である。

(補足：1.画像は、複素平面上の点(R,θ)が画像の表示条件を満足したとき、その点(R,θ)を所定の色で表示している。N-loopの脱出後の(X,Y)を表示しているのでない。ここらへんが混乱しやすいの要注意。)

3図の「内臓」部分でもXとYの規則性と不規則性の混在が見られるが不規則な変化が目立つ。

横軸方向(R方向)のXとYの波形の不連続性は、これらの画像の分解能の不足に拠るものもあると思われるが、画像の感じから言って此れらの画像の不規則な変化は一種のカオス状態になっていることにも拠ると思われる。

この放散虫：Z^3+0.5画像の面白さの要因は、このブログで紹介している他の画像もそうだが此の不規則性と規則性の混在にある、と言えると思われる。

ただ複雑だけの画像や、逆に、ただ単純なだけの画像は退屈で面白くない。
複雑さと単純さの混在こそが画像の面白さの要諦だと思われる。



017 放散虫：Z^3+0.5画像の中のZω点の数？

2014-06-16 12:31:24 | ジュリィア集合の変形：Z^s+C
前記事016で、N-loopを脱出するに要するNをNoとしたとき、No=ωとなるような点Zωの存在を示した(但し、あくまでも「ら線階段」図形からの推定だが)。

点Zωは「ら線階段」の収斂点だから、点Zωの数は画像の中の「ら線階段」の数となる。
記事015において、孫1画像の中の4部分を選び其れらの画像を拡大してみた。

其れらの画像の各々には無数の「ら線階段」があった。
(要するに孫1自身のフラクタル画像が無数に存在していた。)

従って無数のZω点が存在していることになる。

其れらの画像・・・即ち孫1の部分画像・・・を見る限りにおいて、無数は無限と言い換えてもよいと思われる(ここに思考の一つの飛躍があるが)。

その無限の大きさ(濃度)を仮にℵaとしよう。

***

さて孫1画像にはZω点はℵa個あることになるが、Z^3+0.5画像は其のフラクタルな画像も無限個ある。なぜなら或る部分(例えば記事014の子1画像のAの部分)の拡大は無限に可能だからである。その無限の大きさ(濃度)を仮にℵbとしよう。

***

さてZ^3+0.5画像の中のZω点の濃度は ℵa*ℵb としてよいだろうか？

ここらへんのことは私は自身はないが、ともかく Z^3+0.5画像のZω点の濃度については私の興味がある。其れは此のZ^3+0.5画像の魅力の一つである。


016 放散虫：Z^3+0.5画像の「ら線」構造ついて

2014-06-16 09:09:57 | ジュリィア集合の変形：Z^s+C
1.図


2.図


1.図は、放散虫：Z^3+0.5 の孫1 画像を反時計方向に70度回転させた画像である。

2.図は色の説明図である(記事002で説明している。参考のため再掲した。)

1.図から分かるように此の放散虫：Z^3+0.5 の 孫1 画像は「ら線階段」を連想させる画像構造となっている。

そして其の「階段」は或る1点へと収斂している。
この図に書いた数値は其の各「階段」での色を示す数値(カラーコート値)である(2.図を参照)。

1.図から分かることは、此の「ら線階段」は、N-loop脱出時のN値を1ずつ増加させながら、複素平面の或る1点へと収斂している、ということだ。

その収斂点へ向かう程、N-loopを脱出するに必要なN値(No)は増加していく。

そして此の収斂点へ向かう過程は永遠に続くと思われる。
つまり、Noが、いかに大きくなっても其の収斂点には決して到達しないだろうと思われる。

この過程は無限に続くのだが、No値は、一つずつ増加していくわけだから、此の無限の大きさは、いわゆる可算無限だと思われる。

0を含む自然数数全ての集合をωと名づけたとき、この収斂点ではNo=ω表現できると思われる。

そして此の複素平面上の収斂点を便宜上Zω=Xω+iYωと名づけることにすると、「ら線階段」は点Zωへ収斂していく、とも言えそうだ。

さて、問題は此のようなZωは此の放散虫：Z^3+0.5 の 孫1 画像の中に「いくつ」在るのだろうか？　ということだ。

この問題については以下の記事で考察する。

015 放散虫：Z^3+0.5画像のフラクタル性(その4)

2014-06-16 08:13:12 | ジュリィア集合の変形：Z^s+C
下図は、前画像014で示した孫1画像である。この画像の中の5箇所の部分(A～D)を拡大する。それらの画像を便宜上、それぞれ「ひ孫画像1」～「ひ孫画像5」と名付ける。なお各画像の説明は各画像に書いてある。








------------------------------------------------------
記事012より今迄見てきた画像から下記のことが言える。

放散虫：Z^3+0.5 画像の”内臓”部の画像は、3個の同一な画像から構成されている。
そして其の3個の画像自体も、それぞれ、自己相似な3個の画像から構成されている。
そして更に其の3個の画像自体も、それぞれ、自己相似な3個の画像から構成されていて・・・・。このような画像構造が永遠に続いている。

そして又その3個の画像には、それぞれ、1点へと収束していくクネクネと曲がった「ら線階段」が無限に存在する、ということである。

即ち、3個の画像を、どのように拡大していっても、3個の自己相似な画像が永遠に存在する。そして其の画像は、1点へと収束していくクネクネと曲がった自己相似な「ら線階段」が無限に存在する、ということである。

この無限の自己相似性の二重構造が、放散虫：Z^3+0.5　の「内臓」部の画像構造になっている。これは何とも複雑な構造だ。

こんな複雑な構造自体を知らなくても、放散虫：Z^3+0.5　の「内臓」部の画像を見て何となく奇妙で面白い感じをもつのは、我々が此の画像の或る秩序をもった複雑性を直感的に感じ取っているからだろう。