SCILABによる制御系設計 その11

Scilab 11
さてさて、専門的なブログとなっていますが、皆さん理解していますか？
実は、私もあやしいです。
そもそも、複素平面　って　何？
ということや
ラプラス変換　演算子　など　？？？？？　かもしれません。
イメージしやすい例題で解説しても良いのですが、とりあえずscilabの使い方
という視点でやっています。
前回まで、伝達関数表現の　極配置　について見てきました。尾形先生の教科書ではこの後、４−３で「根軌跡上の任意の点に対応するゲインKの値を探索する」、４−４「非最小位相系の根軌跡」４−５「条件安定システムの根軌跡」４−６「むだ時間があるシステムの根軌跡」と続きます。
探した限り、matlabであるrlocusに対応したのがscilabでの対応が難しいため（やろうと思えばやれますが。。。）
ここらへんは飛ばします。（おまえわかってないから飛ばすのか！　という声が聞こえますが）
で、根軌跡によって　当ブログの本題の制御系の設計をやってみましょう。
つまり参考書は４−７「制御システムの性能を補償するための根軌跡によるアプローチ」です。
制御システムは　このやり方は１）モデルが与えられている　そして　２）根軌跡がわかるので　３）補償する制御器を与えてやり　４）MATLABやscilabで評価してやる。
ということになります。　具体的に例題で見ていきましょう。
４−７−１　として　根軌跡による　位相進み補償がまず最初です。。。
zzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzz
寝てますね
あきらめましょう
結局、設計は位相進み補償、位相進み遅れ補償、などを机上でやり
ステップ応答で比較しているのに上記４）をやっているということです。
例題４−１３の結果を示して今回は終わりにします。すみません
s=poly(0,'s');
-->Ht=1.06/(s*(s+1)*(s+2));
-->H=syslin('c',Ht);
-->evans(H,100);
として、まずHtという補償前の前向き伝達関数を与えてその根軌跡を見る。
すると



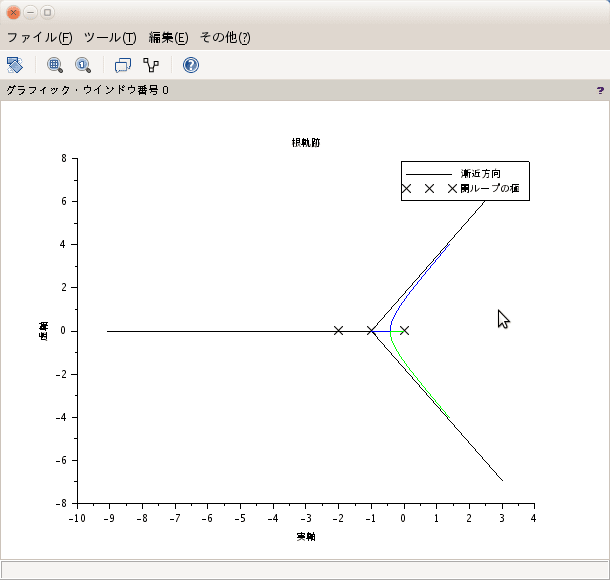
こんな感じの根軌跡が得られる。
補償器を設計して（設計は尾形先生の本に譲る）
->Gt=0.9656*(s+0.05)/(s+0.005);
これが補償器
-->GH=Gt*Ht;
直列にして
-->G=syslin('c',GH);
-->clf()
-->evans(G,100);
警告: evans: 曲線は最初の 2000 個の離散点に丸められています。
あれ　まあ良いか


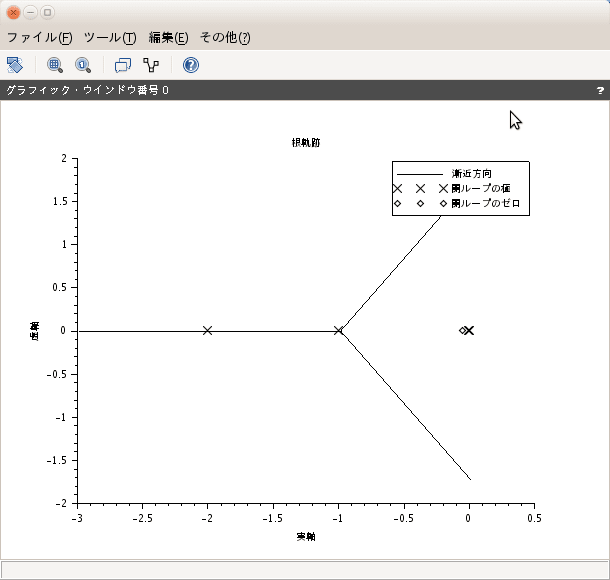
となり補償後のものが得られました。この評価は、ステップ応答の比較をしてみると


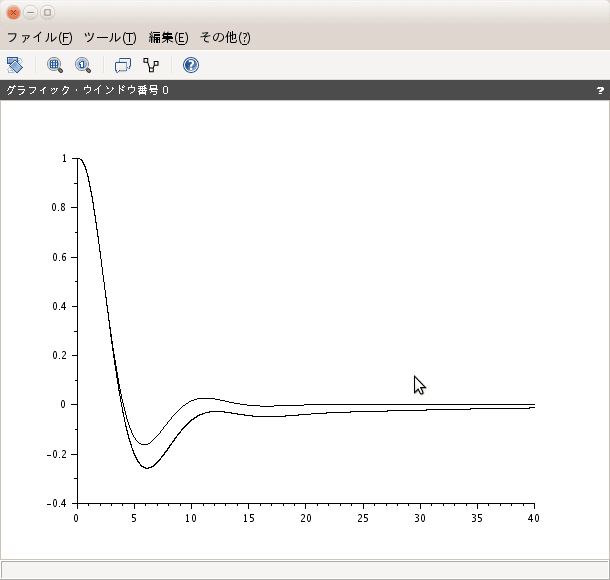
あらら　何かおかしい
今回はここまで　修正してまたアップします。