”数学の秋”〜日本島民よ､たまには頭を使おうじゃないか

　そこで､”数学の秋”に相応しいクイズを紹介しよう。
　｢円周率が3.05より大きいことを証明せよ｣(東大･2003)
　東大入試問題の中でも10本の指に入る有名な問題だそうで､当時のゆとり教育では”円周率は3だと教える”という風評も相まり､世間にあっという間に広まったとされる。
　ハッキリ言って､これが直感ですぐに解ける人はそういないと思う。勿論､フラグ(伏線)を知ってれば簡単だが､知らなければ頭を悩ませる筈だ。そういう私も､三角関数というだけで尻込みしてしまった。

　そこで我ら凡人は､”円周率πが3.05ではなく3よりも大きい事”を､まずは証明しようと試みる筈だ。それに､(数学が苦手な人でも)勘の鋭い人は､”直径1の円周(=円周率π)に関する大小関係を示せばいいのでは？”と考えるだろう。
　そこでまず､”円周>円に内接する正多角形の周”ー①を考える。
　直径1(半径1/2)の円に内接する正6角形は1辺の長さが1/2で辺が6本あるので､その周の長さは3となる。そこで①の定義より､”円周>3⇔円周率π>3”がめでたく導けますね。

最初の難問？〜東大入試に挑戦！

　さてと最初の関門はクリアできたが､3を3.05にするには内接する正n角形の周を3.05より大きくすれば(つまりnを大きくすれば)いい。
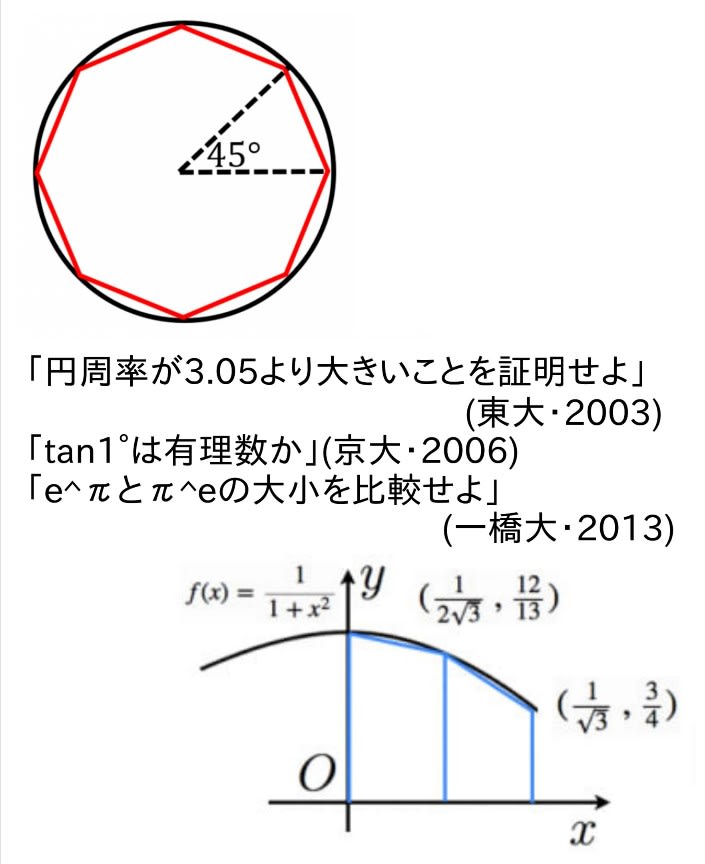
　そこで､正8角形を考える(イラスト)。
　この1辺の長さは(余弦定理を使えば)√(1+1−cos(45°))=√(2−√2)となり､正8角形の周の長さは8√(2−√2)。
　ここで①より､8√(2−√2)<2πとなり､4√(2−√2)<πを得る。左辺を計算すると3.061･･･となるので､円周率>3.05がめでたく証明出来た。
　但し､4√(2−√2)を計算するには電卓が必要だが､4√(2−√2)>3.05を評価すれば済む。
　この不等式は√2<2−(3.05)²/4²と同値で､右辺=1.418･･･と計算でき､(√2の近似が1.414より)確かに成立する。

　しかし､”余弦定理”(b²=c²+a²−2cacosB)なんてクソ喰らえって人も多いだろう。そこで､もっとスマートな証明を紹介する。
　少し高度？になるが､sinxのマクロリン級数を使ったやり方である。
　sinx=x−x³/6+･･･より､f(x)=sinx−x+x³/6とおけば､f’(x)=cosx−1+x²/2､f’’(x)=−sinx+x､f’’’(x)=−cosx+1≥0を得る。
　ここで(f’’(x)とf’(x)の曲線の傾きに注目し)､f’’’(x)の形とf’’(0)=0からf’’(x)≥0,(x≥0)､f’’(x)≤0,(x≤0)が判り､f’’(x)の形とf’(0)=0からf’(x)≥0が判る。故に､cosx≥1−x²/2(マクロリン型不等式)が導ける。
　この不等式にx=π/6を代入し､√3/2≥1−π²/72として､π≥√(72−36√3)=6√(2−√3)を得る。
　故に､π>3.05が示せた。但し､6√(2−√3)の評価(計算)も上で述べた様にやればいい。

　この他にもいろんな証明があるが､”sinの基本公式”(sin(α−β)=sinαcosβ−cosαsinβ)さえ知ってれば､”円に内接する多角形の面積 <円の面積”が利用できる。
　但し､面積による評価は円周の評価よりも緩いし(正12角形でも3<πしか得られない)､3.05より大きい事を証明するには正24角形を使う必要がある。
　半径1の円に内接する正24角形の面積は､sin(π/12)/2×24=3(√6−√2)<πとなり､3(√6−√2)=3.105･･･と計算できるので､π>3.05を簡単に得る(証明終)。因みに､sin(π/12)=sin(π/3−π/4)=(√3/2)･(√2/2)−(1/2)･(√2/2)=(√6−√2)/4ですね。

　しかし､微分も三角関数も嫌だぁ〜という人は､1/(1+x²)の積分を使う証明もある。
　∫[0,1/√3]dx/(1+x²)は､x=tanθとおけば､∫[0,π/6]dθ=π/6と置換できる。
　ここで､y=f(x)=1/
(1+x²)とx軸y軸､x=1/√3で囲んだ部分の面積S=π/6を下から抑える方法です(イラスト)。
　f’’(x)=2(3x²−1)/(1+x)³となり､0≤x≤1/√3でf’’(x)≤0となるので､y=f’’(x)はこの定義域で常に凸。故に､Sを台形2つで下から近似する。
　積分の始点を(0,1)終点を(1/√3,3/4)中間点を(1/2√3,12/13)とすれば､S>(1+12/13)×1/2√3×1/2+(12/13+3/4)×1/2√3×1/2=187√3/624を得る。
　故に､π/6>187√3/624となり､π>3.114・・・>3.05(証明終) 。
　但し､台形1つで近似してもπ>3.031...しか証明できない事に注意です。

　以上､｢高校数学の美しい物語｣を一部参考にして紹介しましたが､三角関数に慣れ親しんでる人には簡単？だったろうか。

tan1°は有理数か？

　次の関門(クイズ)は､｢tan1°は有理数か？｣という､2006年度京大の入試問題で､殆どの受験生が解けなかった？との噂がある問題です。
　これも勘のいい人は､”tan1°なんて無理数だろうよ”と見当をつけますかね。
　無理数の証明には”背理法”を使い､有理数である事を仮定し､矛盾を示す。つまり､tan1°が有理数なら加法定理を用いる事が出来､他の数が有理数である事も導ける筈だと。

　そこでまず､tan1°が有理数であると仮定すると､tanの倍角公式より､tanαが有理数ならtan2αも有理数である。故に､tan2°､tan4°､tan6°､､､も全て有理数である。
　また､tanの加法定理であるtan(α−β)=(tanα−tanβ)/(1+tanαtanβ)より､tanα及びtanβが有理数ならtan(α−β)も有理数となる(有理数とは分数で表される数より明らか)。
　故に､64−4=60より(tan64°もtan4°も有理数なら)､tan60°も有理数となる。しかし､tan60°=√3であり､√3は無理数なので(tan1°が有理数である事に)明らかに矛盾する(証明終)。

　因みに､√3が無理数である事も背理法で証明できますね。まず√3が有理数と仮定すれば､互いに素なp,q(共に整数)を用い､√3=p/qと表せる。両辺を2乗し､3q²=p²ー①と変形すればp²は3の倍数となり､故にpも3の倍数である。
　そこでp=3k,(k:整数)とおけるので①に代入し､q²=3k²を得る。q²は3の倍数でqも3の倍数となる。故に､p,qも3の倍数となり､互いにそである事に矛盾(証明終)。
　但し､平方数が3の倍数なら元の数も3の倍数である事を証明なしに用いたが､3の倍数でない数を2乗し､3の倍数にならない事を示しせば証明できます。

　ここでも､数学力というのは理屈や数学的知識よりも､洞察と直感に負う所が大きい事が理解できますね。しかし､”無理数とは分数で表現できない数”(=2つの整数の比で書き表せない数)という基本的な事を理解してないと前へは進めませんが。
　でも､これが解けない京都大受験者も東大には負けてますね。何とか頑張って､東大を追い抜きましょう。応援してます。

e^πとπ^eの大小を比較せよ

　｢eのπ乗とπのe乗､どっちが大きい｣という問題で､2013年の一橋大の問題ですが､2020年の自治医科大でも出されてます。
　多くの人は､e^πとπ^eを対数(log)をとり､πlogeとelogπの比較まで漕ぎ着けたんではないでしょうか。
　でも､ここからがセンスなんですね。勘のいい人なら､πlogeとelogπをeπで割れば､loge/eとlogπ/πの比較に気付く筈です。
　これは､f(x)=logx/x,x>0の関数として見れば､かなり単純な問題になってきますね。
　つまり､f(x)を微分してf(x)の増減を調べれば､e^πとπ^eの大小に決着が付く訳です。
　f’(x)=((1/x)･x−(logx)･1)/x²=(1−logx)/x²。故に､f(x)はx=e(f’(e)=0)を頂点に凸状になる。つまり､x>eの時はf(x)は単調減少(f’(x)<0)となる。
　また､e=2.7･･･でπ=3.14･･･より､f(e)>f(π)となり､ loge/e>logπ/πにeπを掛けて､e^π>π^eを得る(証明終)。実際に電卓で計算すれば､e^π=23.14･･･>π^e=22.459･･･となりますね。

　因みに､いきなりg(x)=e^x−x^eとして､x=πの時の値を求めた人も多いでしょうが､それだとg(x)の増減を調べるのは難しく､露頭に迷い込みますよ。
　日本全国の医学系大学も､もっと数学の難しい問題を出すべきですね。でないと､汚職の学部とも言われかねない。

　
　以上､有名な3つの大学入試問題を紹介しましたが､いきなり出されて解けた人はそう多くはいないでしょうか。
　多分､NYの司法試験に落ちた小室圭も偽PTSDの元皇族バカ女では､殆どカスリもしなかったでしょうね(笑)。
　そういう私も､後半の2問以外はヒントがなければ､太刀打ちできなかったでしょう。でも､東大の問題は非常にバランスの取れた良質な問題だと思います。
　勿論､フラグ(伏線)を知ってれば､意外と簡単で､錆びついた脳をリフレッシュするには丁度いい問題だったかもです。
　数学とはいっても､全てが堅苦しい事ばかりでもなく､直感と考察で単純にクリアできる部分も沢山あります。
　逆に､数学が得意だと自負自賛してる人も､最初の一歩を間違えると一生を棒に振るほどの危険性を孕んでるとも言えますね。

　｢真犯人フラグ｣が､どうも期待外れで終わりそうなので､少し難しいフラグを用意してみました。
　さてと貴方は何問解けたでしょうか？