ボンバーパズル by 色伝 3

（投稿者 ： 色伝考好）

注意 :
前回のボンバーパズルの最後の問題の解き方の解説を含みます。
まだ解いていない人は、先に前回のボンバーパズルの問題を解いてから読むことをおすすめします。

ボンバーパズルには左のような手筋があります。 この手筋の原理を考えてみると、下のようになります。

黄と赤のマスに入るバクダンの合計は 2個である。つまり、 黄に 1個、赤に 1個。 黄に 2個、赤に 0個。 のいずれかである（赤が 1マスなので、黄に 0個、赤に 2個という組み合わせは不可能）。 黄と緑のマスに入るバクダンの合計は 1個である。つまり、 黄に 0個、緑に 1個。 黄に 1個、緑に 0個。 のいずれかである。 以上の両方を満たすのは、黄に 1個のときだけである。 よって、バクダンは黄に 1個、赤に 1個、緑に 0個となる。

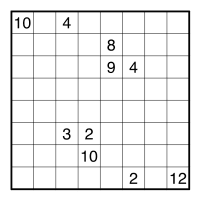
一方、カックロには左のような手筋があります。 この手筋の原理を考えてみると、下のようになります。

黄と赤のマスに入る数字の合計は 4 である。つまり、 黄に 1、赤に 3。 黄に 3、赤に 1。 のいずれかである（ルールから、黄に 2、赤に 2 という組み合わせは不可能）。 黄と緑のマスに入る数字の合計は 3 である。つまり、 黄に 1、緑に 2。 黄に 2、緑に 1。 のいずれかである。 以上の両方を満たすのは、黄が 1 のときだけである。 よって、数字は黄が 1、赤が 3、緑が 2となる。

この二つの手筋を見比べてみると、全く同じ原理だということがわかります。
つまり、本来は同レベルの手筋のはずなのです。
しかし、カックロの手筋は初級手筋どころか、知らなければ簡単な問題ですら一マスも埋まらないというレベルの手筋であるにもかかわらず、ボンバーパズルの手筋は中級以上の手筋なのです。

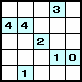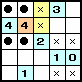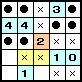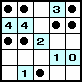
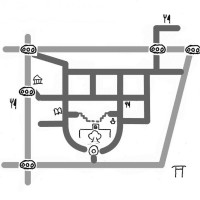
さて、前回のボンバーパズルの最後の問題は、左のようなものでした。 この問題がすんなりと解けた人は少ないと思いますが、実はこの問題も同じ原理で解くことができるのです。

黄と赤のマスに入るバクダンの合計は、紫の数字の合計であり、10個である。つまり、 黄に 6個、赤に 4個。 黄に 7個、赤に 3個。 黄に 8個、赤に 2個。 黄に 9個、赤に 1個。 黄に 10個、赤に 0個。 のいずれかである（赤が 4マスなので、黄には 6個以上のバクダンが入る）。 黄と緑のマスに入るバクダンの合計は、橙の数字の合計であり、6個である。つまり、 黄に 0個、緑に 6個。 黄に 1個、緑に 5個。 黄に 2個、緑に 4個。 黄に 3個、緑に 3個。 黄に 4個、緑に 2個。 黄に 5個、緑に 1個。 黄に 6個、緑に 0個。 のいずれかである。 以上の両方を満たすのは、黄に 6個のときだけである。 よって、バクダンは黄に 6個、赤に 4個、緑に 0個となる。

数は増えましたが、考え方は上の手筋と全く同じだということがわかります。
つまり、カックロで上の手筋を基本レベルの手筋とみなすのは、上のボンバーパズルの問題を簡単な問題とみなすことと同義なのです。
まさにカックロで許容されている手筋の難易度が異常であるということがわかります。

何が言いたいかというと、「こんな難しすぎる手筋を基本レベルの手筋としているカックロなんかより、ボンバーパズルを好きになろうぜー！」ということです。

………。
……。
…。
……だめ？

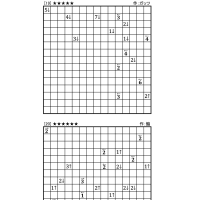
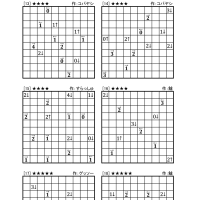
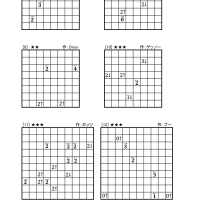
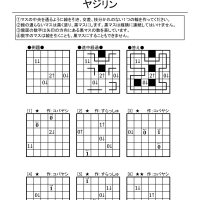
ということで、今回はボンバーパズルです。
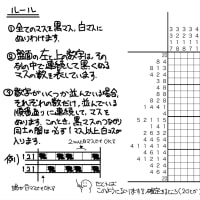
ルールは、一回目の記事を参照してください。

（クリックすると大きな画像が表示されます。）