スラローム by フェニックス 2

（投稿者：フェニックス）


スラロームのペンパ本が発売されました。依頼が来たので15問作ったら3問載りました。これを多いと見るか少ないと見るか…

出来の悪い問題でも、作ったものはとりあえず送ったから、多かったことにしておこう。


で、ニコリに問い合わせたところ、ボツった問題が今後別のところで使われる可能性はほとんどないとの事だったので、許可をもらって一部をここで公開することにしました。（スラロームのルール）


（クリックすると大きな画像が表示されます）

以下はパソコンで遊ぶ人向けです。ぱずぷれを利用させていただきました。（問題は上の画像と同じものです）

スラローム 10×10 （1）
スラローム 10×10 （2）（一部改変）
スラローム 10×18 （1）
スラローム 10×18 （2）
スラローム 14×24 （1）
スラローム 14×24 （2）（一部改変）


見た目重視派の僕としては、10×18 （1）みたいな点対称配置の問題で、ド真ん中に発着点を置けないことが、時々非常に苛立たしく感じます。ペンパ本用でサイズが指定されていたので指定通りのサイズで作りましたが、本音を言えば奇数×奇数の方が作りやすいんですよね…

しろまるくろまる by 色伝 3

（投稿者 ： 色伝考好）

おかげさまで、大学祭は無事終了しました。
来ていただいた方は、本当にありがとうございました。

さて、パズル同好会は、大学祭に関する皆様の感想をお待ちしております。
今後の活動の参考にさせていただきたいと思っています。
ご感想・ご要望などがありましたら、ぜひこのブログのコメントにお書きください。
コメントはどの記事にしていただいてもOKです。

特に、冊子のパズルについては難易度も種類も大きさも問題数も手探り状態です。
「おそらく読者はこういうパズルを望んでいるだろう」という仮定の下で作られた冊子であり、その仮定が正しいかどうかは不明なのです。
「簡単な問題を増やしてくれ」とか、逆に「もっと難しい問題が解きたい」とか、「この種類のパズルが解きたい」とか、「大きなサイズの問題が解きたい」とか、どういったものでもかまいません。
冊子を買っていただいた方は、ぜひとも感想をお聞かせください。
来年も冊子を作るかどうかはわかりませんが、作るときにはその参考にさせていただきたいと思っています。

……………………。

……以上で業務連絡終了。
ここからはしろまるくろまるのターン！！

しろまるくろまるには、外枠に接するマスに関するある制約があります。
その制約は、前回説明した手筋以上の強いものです。
それを用いれば、前回の5番の問題もたちどころに解いてしまえるのです。

その制約とは、以下の通り。

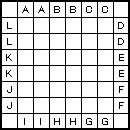盤面が偶数マス×偶数マスの場合、たとえば左の図においては同じ文字のマスには同じ色の丸が入ります。

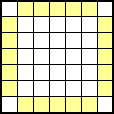盤面が奇数マス×奇数マスの場合、たとえば左の図においては黄色のマスに入る○と●の数は、それぞれ奇数個になります。 ただし、非常に特殊なケースですが、奇数マス×奇数マスの場合、外枠のマスすべてが同じ色の丸になるという例外もあります。 とはいえ、そういう問題はまず見ればわかるので、意識して覚えておく必要はありませんが。

普通に解いているだけではまず気づくわけがない上に、教えられたとしても単純な試行錯誤ではなぜそうなるのか証明することができないという、ひどい手筋です。
こんな手筋を使わないと解けない問題を作る人の気がしれませんよねー。

……。

では、早速証明に入ります。
今回の証明方法は、ペンパ石くんとフェニックスくん考案のものです。
私が考えた証明方法は別にあるのですが、ペンパ石 & フェニックス証明の方が説明しやすいので、今回はこちらで説明することにします。
前回の記事の手筋は既知のものとします。

まずは、左の問題について考えてみます。

○と●の境界に線を引きます。 すると、線は外枠からスタートしてすべての交差点を一回ずつ通って外枠へと出ることになります。 ここで、線の通り方について、詳しく見てみます。

交差点を赤と青で市松模様に塗ります。 すると線は、 …→赤→青→赤→青→赤→青→… のように赤と青を交互に通ることになります。 盤面のサイズが偶数マス×偶数マスの場合、交差点は奇数個×奇数個となります。 すると、左のように塗った場合、赤が青より1マス多くなってしまいます。 つまり、すべての交差点を一回ずつ通るためには、線は赤で始まり、赤で終わらなければならなくなってしまいます。

赤で始まり、赤で終わるということは、左の図の同じ文字のマスには同じ色の丸が入らなければならないのです。

	奇数マス×奇数マスの場合についても、同じように考えてみます。

奇数マス×奇数マスの場合、交差点は偶数個×偶数個となります。 すると、赤と青の数が同数になります。 つまり、線が赤から始まった場合必ず青で終わり、線が青から始まった場合必ず赤で終わることになります。

赤から始まり青で終わる、もしくは青から始まり赤で終わるということは、左の図の黄色のマスに入る○と●の数は、それぞれ奇数個にならなければならないのです。

以上です。
わかりやすさを優先し、できる限り文章量が少なくなるように意識して書いたため、あえて説明を省いている箇所があります。
各自で補いながら読んでください。

ということで、今回はしろまるくろまるです。
上の手筋を使ったり使わなかったりします。

しろまるくろまるのルール（ant's PUZ-T）

（クリックすると大きな画像が表示されます。）

しりとり

（投稿者：D-duck）

十一月祭でパズル同好会の教室にお越しくださったみなさん、ありがとうございました。
楽しかったよー、また来年も来るからねー、とお声をかけてくださったお客さんもいて、とても嬉しかったです。

そして。
四日間頑張ってくれた会員さん、本当にお疲れ様です。
また打ち上げでもしましょう。


ところで、教室にしりとり書き込みスペースがあったのは覚えているでしょうか？

今日はその結果をパーッと貼ってみましょう。
諸事情により一部伏せている言葉もありますが、決して決して詮索しないように。

ではご覧ください。


しりとり→リサージュ図形→イクラ→ランタノイド→どぶろく→クリスマスキャロル→ルイス・キャロル→ルーレット→トリチェリー→リーマンブラザーズ→ズッキーニ→虹→ジグソーパズル→ルミナリエ→エコ→コイズミキョウコ→コバヤシサチコ→コウヤマタカヒコ→コンドウマサヒコ→コイケエイコ→ココリコ→子→子猫→小太鼓→コロッケ・→けむし→しゅうまい→いんげんまめ→めだまやき→きゅうり→りんごじゅーす→すけべ→ベル研究所→陽動作戦→ンゴマ→マインスイーパ（上級136秒です）→パズル同好会→イタロカルヴィーノ→ノスリ→リプシッツ連続→クラシス→推理小説研究会→イソジン→ンジャメナ→ナン→ンゴロンゴロ国立公園→ンジャロ→ロバート・ラングドン→ンギグリ語群→ンクルマ→マグダラのマリア→亜細亜→アルメニア→アルバニア→アルジェリア→アーネスト・ヘミングウェイ→ε-δ論法→浮世絵→エクアドル→ルベーグ→グレートブリテンおよび北部アイルランド連合王国→クルンテープ・プラマハーナコーン・アモーテラータナコーシン・マヒンタラーマッタヤー・マハーディロックポップノッパラットラーチャタニーブリーロムウドムラーチャニウェートマハーサターンサッティットサッカタッティヤウィサヌカムプラシット→トビウオ→甥っ子萌え→エンドウ豆→メンデル→ルービックキューブ→V3きりもみキック→クジラ肉→黒澤明監督→クリック→クロック→クロネッカーのδ→δευｓ→Σベスト→トンガ→ガーネット→トリグリセリド→ドストエフスキー→イジングモデル→ルール→ルーブル→ルノワール→ムワッヒド朝→ウンウンオクチニウム→ムルムル→ルベーグの収束定理→リウビルの定理→留数定理→リプシッツの定理→リンデュンの定理→リーマンの拡張定理→リーマンの写像定理→立方体→陰函数定理→リーマン予想→ウリゾンの補題→インジウム→無理数→ウラジミール・ナボコフ→フビニの定理→リンカーン・ライム→無量大数（10^（68））←まちがえてるよ～→ウィリアムゴールディング→群準同型→因数分解→イソプロピルベンゼンペルオキシド→どじっ子もえ→エネルギー保存の法則→クローンの法則→くら→ラジウム→ムッソリーニ→ニトロセルロース→スイス→スイス→スイス→ストレス→スライス→スタニスワフ・レム→無限次元ベクトル空間→ンドゥール→ルジャンドルの未定乗数法→ウィリアム・トレヴァー→アイザック・アシモフ→フィリップKディック→クリストファー・プリースト→トルーマン・カポーティ→イーガン→ンゴロンゴロ動物保護区→クノー→ノーフォーク→玖渚友→モルモット→トリチウム→村紗水蜜→蜜蜂→遅延時間→間奏→上田馬之介（助かも）→ケリー・リンク→九字刺し→シュークリーム→ムース→ストロベリーショートケーキ→キサントプロテイン反応→応答速度→ド・ブロイの物質波→波動関数→ウラジミール・クラスノーホフ→フーリエ級数展開→インピーダンス→スイカ→カ→カカ→カイリュー→ウマイボウ→ウサギ→ギニュー→ウリボウ→うきわ→わんこう→○○○→ちくわ→○○○○→ツンデレ→レモネード→ドン小西→下着→ぎょうざ→ざんしゅけい→いす→すいぎょうざ→ざくろ→○○→リーチ→チロルチョコ→穀物→物理演算→算盤→盤上→うな牛→牛若丸→ルドルフ数→ウォルフガンブ・アマデウス・モーツァルト→トマト→トマト→トマト→トマト→トマト→トマト→唐辛子→素人→トマト→とんぼ→ボート→時→キットカット→十寸→金閣寺→ジェイムズ・ジョイス


「ちゃんとつながってんの？」とか「『ん』で復活してるよ…」とか「理学部容赦しないのね」とか「英米文学、よう頑張った」とか、色々と突っ込みどころはありますが、まぁ、大目に見てあげてくださいな。


ついでに裏メニューの方も貼っておきます。
省略部分はみなさんの豊かな想像力で補ってください。


トマト→トマト→トマト→…→トイレット→トマト→…→トースト→トレンチコート→トマト→…→トロイアット→トランスポート→トロント→トマト→…→トメイト→トマト→TOTOのウォシュレット→トマト→トマート→トマト→…→ト・マ・ト→トマト→…→トワイライト→トロイメント→トマト→…→トリト→トマト→…→トマト


パズル同好会的には、トマト以外の言葉が入っているという点で未熟なしりとりですね。
来年はもっと熟したトマトを目指しましょう。


それでは、来年もよろしくどうぞ。

美術館 by 色伝 2

（投稿者 ： 色伝考好）

明日から11月祭スタートです。

パズル同好会の企画の場所は、京都大学のサイトの吉田南構内マップを参照してください。
「吉田南4号館」という建物でやっています。
11月祭の詳細については、11月祭公式サイトを参照してください。

さて宣伝はこれくらいにして、今回は美術館です。
完全に見た目重視です。
解き味重視の美術館が解きたい方は、前回の美術館をどうぞ。

美術館のルール（webニコリ、フラッシュ版）
美術館のルール（webニコリ、テキスト版）

（クリックすると大きな画像が表示されます。）

以下は、パソコン上で遊びたい方用です。
カンペンを利用させていただきました（問題は上の画像と同じものです）。

• 美術館 01（かんたん）
• 美術館 02（むずかしい）
• 美術館 03（ふつう）
• 美術館 04（むずかしい）
• 美術館 05（むずかしい）
• 美術館 06（むずかしい）
• 美術館 07（ふつう）
• 美術館 08（むずかしい）

P.S. ゴマ卵さんへ

コメントでのパズルの問題、ありがとうございました。
あの2問には、言葉では言い表せないほど感激しました。
本当にありがとうございました！

そうだ、京都大学に行こう。

（投稿者：D-duck）

今週の11月20日（金）から23日（月）まで、京都大学ではNF（November Festival：十一月祭）が開催されます。

そして今年も、われらが京都大学パズル同好会は、教室をお借りして企画を行います！

教室は、吉田南構内の4共13。

その名もふにゃり、

「Ｐ(⊃ＮＮ)^(90゜)＜ｅ」

えっ？
意味がわからないですって？
そうでしょうね。
正直自分もわかりません。

まあ、⊃ＮＮの部分を右に90゜回転させてみましょうか。


Ｐ
Ｕ
Ｚ
Ｚ
＜
ｅ


どうです？
何かが見えてきたかもしれないような気がしないでもないけど、うん、ひょっとして、もしかして、多分、あれってあれだよね…？的な感想を抱いてもらえれば本望です。


会場では、知恵の輪や各種メカニカルパズル、ルービックキューブなど、いろいろなパズルで遊べます。

また、クロスワード、数独、迷路などのペンシルパズルも自由に解けます。

更になんと、パズルの説明をしてくれる優しいお兄さん、お姉さんまでついてくるという充実のサービスっぷり。

今すぐ行かなきゃっ！と思ったあなた、三日ほどフライングです。
まだまだ宣伝は終わってませんよ。

そして今年は、同好会員特製のパズル冊子がバージョンアップ！

パズルの種類もページもどどんと増えて、印刷・製本は業者さんに頼んだきれいな仕上がり。
これでお値段たったの200円。

普通の人なら三ヶ月は楽しめます。


ええ、もう行くしかないですよね。
待ちきれませんよね。
待っててくださいあと三日。

以上、ぜひとも週末は京大へ、という話でした。