都立数学 大問3の三問めは解くべきか

[2022年1月17日 更新]

都立高校入試の数学では、各大問の最終問題が難しいことはこのブログで何べんも言ってきた。

その中でも取りやすいのはどれかと問われたら「大問2か大問3」と答える。

◆正答率を見れば明白

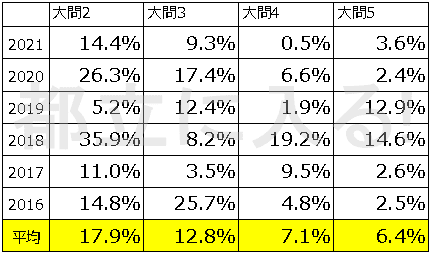
この表は過去6年の都立高校入試数学、各大問の最終問題の正答率を示したもの。

大問2と大問5は二問目。

大問3と大問4は三問目。

年度によって異なるが、平均すれば易しい順に

大問2→大問3→大問4→大問5　となっている。

大問2は証明問題なので、「そもそも証明問題は無理」という受験者が一定数いる。だが正答率を見ると異常なほど低いこと(1桁パーセント)はほぼない。

対策さえすれば、途中点も含め点を稼ぐことができるのだ。

◆大問3は取れるか

では同じように、大問3の三問目は解けるか。

出た問題は、

2021年度　1次関数…三角形の面積が等しくなる点Pのx座標

2020年度　2次関数...四角形の面積が三角形の4倍となる点Pのx座標

2019年度　1次関数…三角形の面積が2倍となる点Pのx座標

2018年度　2次関数...直線が原点を通るときの点Pの座標

2017年度　1次関数…三角形の面積が2/5倍となる点Pのx座標

2016年度　2次関数…三角形の面積が3倍となる点Pのx座標

1次関数が2年連続で出たことはないので、2022年度は2次関数(2乗に比例する関数)なのは確実。

また今年は平均点を少し上げたいだろうから、大問3の三問目もやや易しい可能性がある。すると傾向は変えてこないだろうから、「三角形〇〇〇の面積が□倍になるような点Pのx座標を求めよ」のパターンの可能性が高い。

数学で80点以上、偏差値60台半ばを狙うのなら大問3の三問目は解く価値があると見ている。

◆x座標をtと置け

点Pの座標を求める問題では「点Pのx座標を文字tと置き、y座標はtで表す」のが鉄板。

x座標、y座標を2種類の文字で置くのは推奨しない。式が2つ必要で煩雑になるからだ。

またy座標をtと置くと面倒なことになる。やってみるといい。

都立入試の関数では「x座標をtと置く」が手堅い。覚えておくべし。

都立に入る!　ツイッター 役立つ情報。ミンナニナイショダヨ

@toritsukoko