３次元空間を考える

　前回から少し時間が経ってしまいました。春になって、気温が上昇してきましたので、農作業の仕事が忙しくなってきました。病気のリハビリを目的として始めた無農薬有機野菜栽培が、ここ３年くらいで１００坪ほどの農園に拡大してしまい、草取りや土造りに追われています。

　何せ、私の住んでいるところから１５Km程離れた農地で、数十年の間放置していた所です。そのため、草や木の根の除去、畑の区画整理（一区画５から１０ｍの畦）に多くの時間を今までに費やしています。しかも、家から離れているために農機具を買うことも出来ず、ただひたすらスコップと鍬及び素手での作業が中心となっています。

　今後は、この農作業の合間をぬってブログの更新をしていく予定です。

　今回は久々に一日中雨が降っていますので、前回の続きとして私の頭が「ボケ」てしまわないうちに、この物質世界の話を書くことにしました。


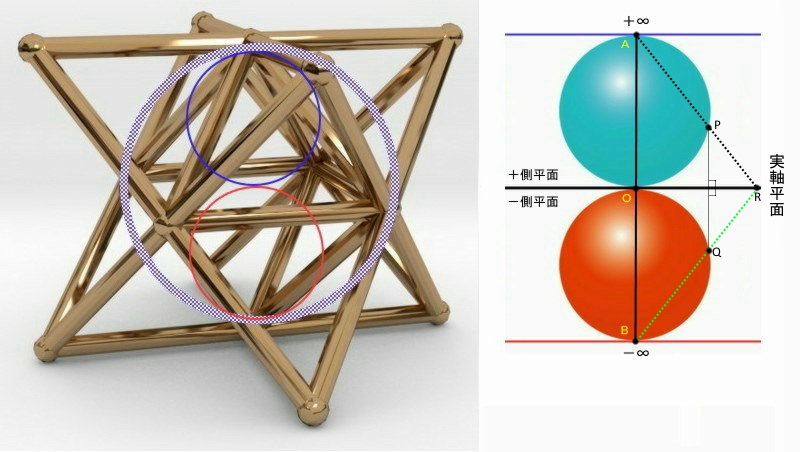
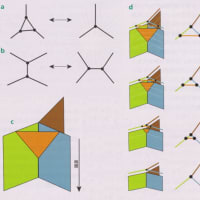
図：マカバの中の空間

　まず上の左側の図の説明に入ります。この図の中にあるの正八面体を球体（外接球）として考えていきます。この時、私たちが地表面として認識している場所は正八面体の中心部分（正方形）、すなはち外接球の赤道面になります。この表面上の場所が人類に与えられた立体的空間として感じることの出来る場所です。

　この中心部分（正方形）の平面とは別に、マカバのの底部と上部のクロス（Ｘ）した平面に関して、この左図では、正八面体の上下の特異点（＋∞・―∞）に接する円（球体）を描いています。
　
　次に右図を見て下さい。この図は、左図の正方形の中心をＯ（特異点＝＊）として、この点Ｏを挟んで上下に二つの球体を配置しています。そして、点Ａ・Ｏ・Ｂの３つの点はいずれも特異点になっていることに注意してください。
　点Ａ・Ｏ・Ｂを含む青・黒・赤の特異点を含む平面は、「＋∞・＊・－∞」という特殊な壁（ブレーン）になっています。そして、点Ａと点Ｂはどちらとも特異点ですので、点Ｏと同じ扱いが出来そうです。すなはち、点Ａでは青球の上に赤球が、一方点Ｂでは赤球の下には青球の特異点として二つのブレーンが張り合わされているのです。

　例えば、点Ａから青球面上の点Pを覗いてみることにします。すると、右図に描いていますように実軸平面上の点R（上側）に点Pの情報が描かれます。しかし、点Aと点Bは同じ場所と見なせますから、点Bから赤球面上の点Qを通った点R（下側）は重なってしまいます。

　この例えから推測出来ることは、我々人類が認識している側が青側であるなら、その世界に映し出されている事象（ホログラム）はプラス側平面の事象ということになります。

　さて、今度は青球面上の点Pが点Oから点Aに向かって反時計回りに回転していることにします。すると、実軸平面上に描かれた軌跡（時間）は点Oからスタートし、点Pが点Aに非常に接近した時には一瞬にして無限大に離れた距離に到達していることになります。だから、特異点である点Aに到着した瞬間には実軸平面上では無限大の速度に達しているはずです。このことは、運動エネルギー（E＝1/2ｍｖ^2）も無限大になっていることを意味します（ｖ＝速度）。

　このエネルギーの問題を解決するために導入された定数が、光速（ｃ＝30万Km/s）であり、この光速ｃが繰り込まれたエネルギーの式が「E=ｍｃ^2」なのです。この式の意味することは、光速で運動する物質は質量が０であり、反対に質量が０である物質は光速で運動するということが定義されたことになります。

　次に、赤球面上の点Qが点Oから点Bに向かって時計回りに回転していることにします。点Pの時と同様に考えることで、光速とエネルギーに関しての結果が同じになることがわかります。ただし、異なる点はホログラムがプラス側平面の事象とマイナス側平面の事象との違いです。

　ここで、実軸平面上に映し出されたホログラムは、光としてしか認識出来ないことが解ります。すると、目の前に映し出された３次元的な物体には、はたして質量が存在しているのでしょうか？

　また、プラス側平面とマイナス側平面のホログラムと実軸平面上の物体との関係はどのようになっているのでしょうか？


　今回は、疑問を投げかけたところで終了します。次回の更新までには数日掛かりそうですから、その間、皆さんもこの問題に取り組んでみてください。