前回、突然にペンローズ・ダイアグラムすなはちペンローズ図を持ち出したため、話がいきなり難解になってしまい、誠に失礼しました。
それで、このペンローズ図について易しく説明をしてくれている書籍を探したのですが、専門書以外にはあまり一般に出回っていなくて、私の書棚からペンローズ関連の書物を探してみました。
すると、講談社のブルーブックに「ペンローズのねじれた四次元」という竹内薫氏がお書きになっている本が見つかりました。
今回は、「ペンローズ図とは?」という題でブログに書かせていただきます(ほとんど抜粋編集)。ただし、この書籍から、ペンローズ図に必要な部分を抜き出しています。いくらかでも時空構造を理解するための、手助けになってくれたらいいなと思っています。
ペンローズ図というのは、無限に遠い所を有限の所にもってきた図のことを言う。ペンローズ以前には、この図を描いた人はいなかったわけだから、この発明は、実は、大変なことなのだ。 普通の時空図をペンローズ図に変換する数式は、ものすごく複雑で、かなり数学をやった人でも、「どうして、こんな変換に気がついたのか!」と悲鳴をあげるに違いない。
一般相対論の教科書のバイブルとして有名で「電話帳」の異名を取る「Gravitation]
という分厚い本には、ペンローズ図について、次のような記述がある。ペンローズは一般相対論の業績があまりにも多く、他人が思いつかないような図を描くので、どれもこれも「ペンローズ図」になってしまう、というわけ。
ところで、なんで無限の点を有限のところにもってくる必要があるのか?
実は、それには、れっきとした物理学的な理由がある。
ここでは、技術的な問題に深入りはできないが。結論から言うと、ハーマン・ボンディやペンローズらによって、うまい方法が考えだされた。ペンローズ図は、そのような物理学者たちの重力場との悪戦苦闘の過程で生れたのであった。
それでは、ペンローズ図の読み方を伝授しよう。
この図の見方は、おそらく、物理学者でもわからない人がいるのだと思う。といっても、いくつかの決まりさえ覚えれば、そんなに難しいものでもない。メルカトル図法の地図を平気で読んでいる人なら、大丈夫、読める。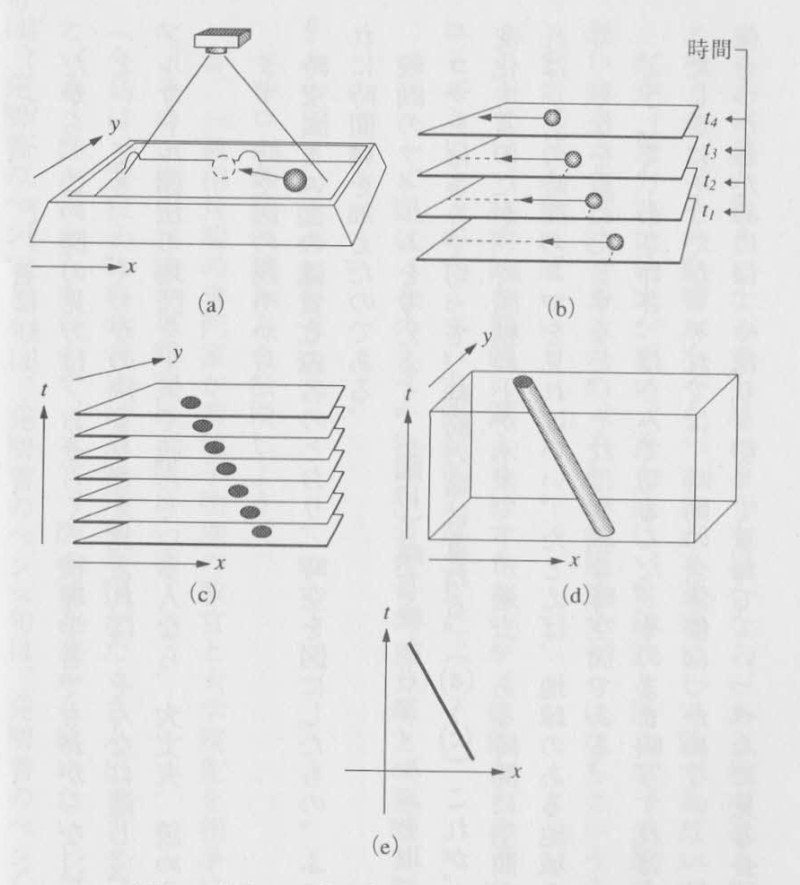
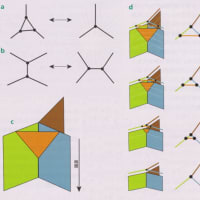
図1:フィルムの重ね図
まず、時空図の説明から始めよう。時空図というのは、その名のとおり、時空を図にしたもの。ふつうの地図は、空間図だが、それに時間軸を加えたのである。
映画のフィルムを考えよう(図1)。映写機からフィルムを取ってきて、フィルムの一コマ、一コマをはさみで切って、時間の順に重ねる((a)~(c))。これが、時空図である。空間の様子が変化するのだが、時間軸の上が未来で下が過去。
ある時間に空間がどうなっているかを知りたければ、その時間のコマを見ればいい。たとえば、地球のある地域の歴史をフィルムに撮っておいて、それを重ねたとすると、それは立派な時空図である。
もっとも、フィルムの場合、四角形なので、二次元になっていて、図が見づらい(d)。そこで、多くの場合、二次元のフィルムの軸を一つだけ残して、単純化する。だから、時間軸のほかには、空間軸が一つだけになる。通常は、縦軸が時間で横軸が空間だ(e)。
時空図は、上下左右に無限に大きいと考える。
ここで、原点にある電球から四方に照射された光がどう描かれるかに注目してほしい。光は、時間とともに遠くまで達する。光速は約30万キロメートル毎秒だから、時間軸の目盛りを1秒、空間の目盛りを30万キロメートルにしておけば、光は、傾きがプラス・マイナス1の直線として表される。角度が45度である。
この光の軌跡のことを「光円錐」(Light cone)と呼ぶ。どうしてかというと、フィルムの空間次元をもとの二次元に戻すと、光が原点から円錐状に出ているから(図2)。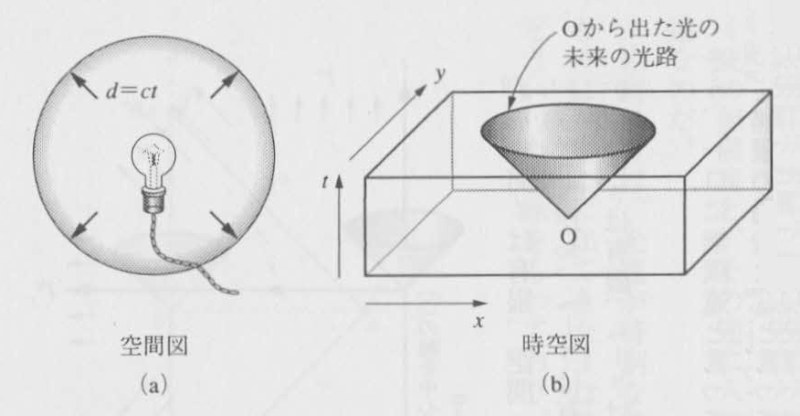
図2:光円錐の図
それでは、いよいよペンローズ図である。
普通の時空図は、アインシュタインのチューリッヒ工科大学時代の数学の先生であったヘルマン・ミンコフスキーの名をとって、「ミンコフスキー図」と呼ばれている。このミンコフスキー図では、無限遠は無限遠にあるので、紙の上に描いたのでは見えない。無限遠で時空がどうなっているかは見ることができないのだ。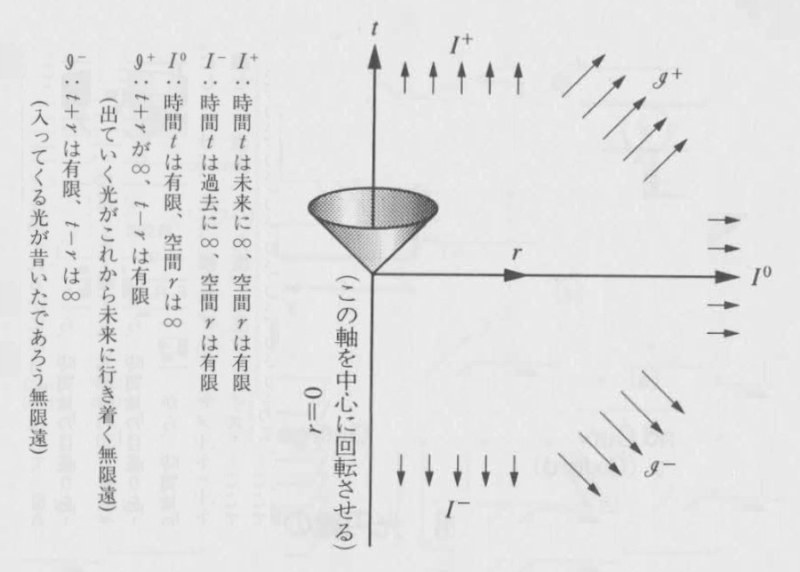
図3:ミンコフスキー図
平らな時空のミンコフスキー図には、いくつかの重要な無限遠の方向がある(図3)。そう、一口に無限遠と言っても。どっちの方向に遠いかで話が変わってくる。ここで、無限の未来と無限の過去と空間的な無限遠はいいとして、最後の二つがくせものだ。これは、無限の未来と空間の無限遠(右斜め上方向)と、無限の過去と無限遠の空間(右斜め下方向)だ。原点から出ていく光が行き着く先の無限遠と、その逆に入ってくる光が出発した無限遠である。二つとも、光にとっての無限遠なのだ。
相対論では、光速が特別な役割を演ずるため、「光の観点からの無限」を考えるのである。ちなみに、ここに出てきたIは英語のinfinity(無限)の頭文字で、肩の添え字は、未来(+)、過去(-)などといった意味をもっており、最後の二つの文字は「スクリー」と読む。時空の無限は、未来、過去、空間、二つのスクリーというわけである。
さて、いよいよお待ちかねのペンローズ図だ。
ミンコフスキー図をペンローズ図(図4左)にすると、tとrが、ψとξに変数変換されて、五つの無限遠点が、有限の距離にきたことがおわかりだろう(ψはギリシャ小文字のプサイ、ξはクサイ)。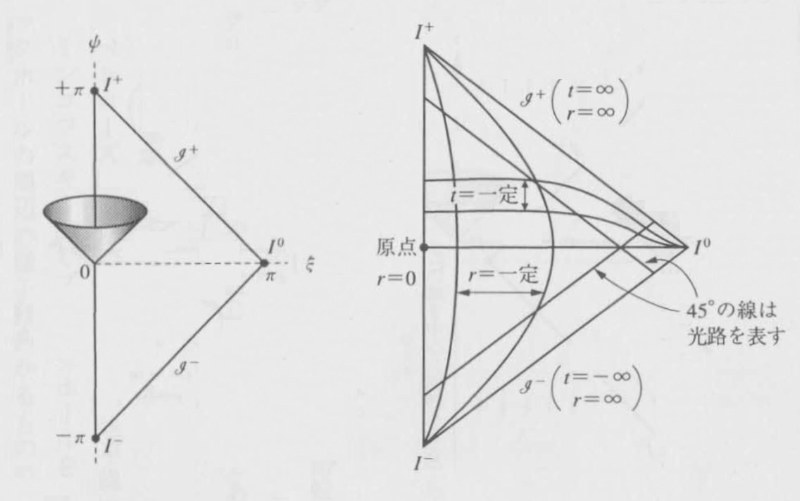
図4:ペンローズ図と拡大したペンローズ図
ここで、注目していただきたいのは、光の経路が、ミンコフスキー図と同じく、45度の角度のままな点だ。これは、角度を変えない変換という意味で「等角」変換と呼ばれている。ペンローズ図への変換は、光円錐をそのままに保つ特殊な変換なのである。
ミンコフスキー図に方眼をいれると、それがペンローズ図でどうなるかがわかる。時間tが一定の線と空間距離rが一定の線を確認してほしい。
これでわかることは、ペンローズ図というのは、ようするに、二つのスクリーを無限遠から有限のところまでググーツともってきてしまったものということだ。頭の中で想像してみてほしい(図4右)
つまり、光が進む方向を動かさないように固定して、光にとっての無限遠を有限の距離にもってきてしまったのである。ある意味で、全宇宙を小さな三角形の中にぐーっと縮めてしまったのである(正確には、三角形の縦軸を中心に回転させたもの。さらに言えば、そうやって回転させたとしても、空間の次元を一つ無視しているのだが)。
これは、ようするに、宇宙の無限に大きい時空図をぐぐーっと縮めて三角形の世界にして、全体像を俯瞰(ふかん)しているのだ。こうすると、宇宙のどこかで起こった事件が別の地点にどのような影響を及ぼすか、というような因果関係が明確になる。
ただ、ちょっと注意が必要だ。今、宇宙を三角形に縮めると言ったが、通常の時空図で四次元時空を二次元時空に簡略化して描いているのと同様、ここでも空間の三次元を一次元に簡略化してある。それがξ(クサイ)方向だ。空間を二次元にするには、ψ(プサイ)軸を中心にぐるっと一回転させてやればいい。
三角形を回転させると、円錐を二つくっつけたような形になる。アイスクリームコーンのコーンを二つ丸いところで接着したような形。宇宙を二つの合わせアイスクリームコーンの中に封じ込めたわけである。
ペンローズ図を使って、「事象の地平線」と「ホワイトホール」を考えてみよう。
ミンコフスキー図でブラックホールを眺めていても、あまりよくわからない。というか、ブラックホールの周辺の様子はわかるものの、遠くでどうなっているのか、中はどうなっているのか、あまりよく見えてこない。
そこで、ブラックホールをペンローズ図にすると、驚くべきことに、ブラックホールの大局的な構造が手にとるように見えてくる(図5)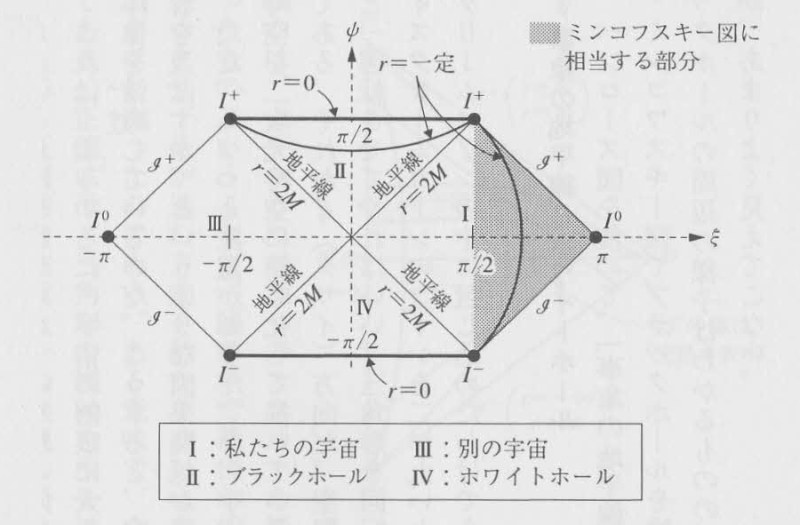
図5:ブラックホールのペンローズ図
この図の見方は少々難しい。
まず、一番右の漢数字Iと書いてある領域に注目していただきたい。これは、さっきやったばかりの三角形のペンローズ図を拡張した領域と考えてほしい。この部分は、ブラックホールの事象の地平線(r=2m)の外側である。
次に、r=2mという線を越えて領域Ⅱに入ると、そこはいわばブラックホールの中。もう外には出られない。
領域IとⅡは、それぞれ、領域Ⅰがブラックホールの外部で領域Ⅱが内部に相当するわけだ。原点からブラックホールに向けて光を発射すると、それは、シュヴァルツシルト半径(r=2m)を通って、ブラックホールの中に入って、やがて、特異点(r=0)に達する。
ここで、ブラックホールの内部Ⅱでは、tとrの役割が逆転していることに注目してほしい。領域Iでは、距離rが一定の線は上端から下端に伸びていたが、領域Ⅱでは、左端から右端に伸びている。
これは、物理的には、べつに時間と空間が逆転したわけではない。だが、領域Iでは時間が進むのを止められなかった人間は、領域Ⅱでは、特異点に向かって進むのを止められない。そう考えれば、ある意味で、空間と時間の役割が逆転したのだと思ってもらっても差し支えない。
特異点のr=0が、上下に二本ある線で表されているが、これは、無理やり無限遠点を有限のところまで引っ張ってきてしまったため、そのしわ寄せを喰って、特異点が間延びしたように見えるだけのこと。特に意味はない。
むしろ、問題は、領域ⅢとⅣの存在である。こりゃあ、いったい何だ?
実は、これがペンローズ図の威力なのだ。ペンローズ図は、無限の遠くまでも含めた全体像を見せてくれる。
領域Ⅳは、ブラックホールの時間を反転したもので、「ホワイトホール」と呼ばれている。ブラックホールの正反対の性格をもっていて、ホワイトホールからは、なんでも出ることはできるが、決して中に入ることはできない。
図の一番下の特異点を出発した光は、やがて、地平線を越えてホワイトホールの外に出てくる。領域Ⅳから領域Ⅲへは一方通行なのである。また、領域Ⅳから領域Iに出ることも可能だ。
だが、もし、われわれが領域Iに住んでいるとするならば、われわれは、決して領域Ⅲに行くことはできない。それは、われわれとは因果関係をもたない「別の宇宙」なのである。
今回は、長い文章になってしまいましたが、図も多く掲載しましたのでお許しください。「ペンローズ図」に少しは慣れたでしょうか。次回も出てきます。
最新の画像[もっと見る]
-
 タイムトラベルとタイムマシン?
10年前
タイムトラベルとタイムマシン?
10年前
-
 パウリの夢の数式に「虚数」が生み出された!
11年前
パウリの夢の数式に「虚数」が生み出された!
11年前
-
 「微細構造定数」137とパウリ&ユング
11年前
「微細構造定数」137とパウリ&ユング
11年前
-
 宇宙インフレーション 超弦理論
11年前
宇宙インフレーション 超弦理論
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
 相対性理論とローレンツ対称性
11年前
相対性理論とローレンツ対称性
11年前
-
 宇宙の起源に新説か?
11年前
宇宙の起源に新説か?
11年前
-
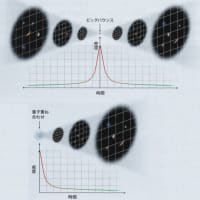
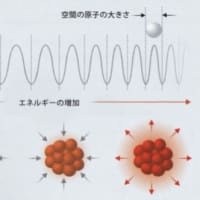 宇宙の始まりは「ビッグバウンス」?
11年前
宇宙の始まりは「ビッグバウンス」?
11年前
-
 「スピンの泡」が時空に対応する、ループ量子重力
11年前
「スピンの泡」が時空に対応する、ループ量子重力
11年前










※コメント投稿者のブログIDはブログ作成者のみに通知されます