算額(その1179)
時岡郁夫:趣味の数学問題集
http://i4.gmobb.jp/tokioka/tokioka_mondai/index.html
キーワード:円3個,正方形
A問題 57. 一辺の長さが 1 の正方形の中に大円 2 個,小円 1 個を容れる。3 つの円はそれぞれが正方形の 2 辺に接しており,小円はさらに 2 個の大円にも接している(大円 2 個は交差している)。
3 つの円の中心を結ぶと正三角形になるときの,小円の半径を求めよ。

正方形の一辺の長さを a
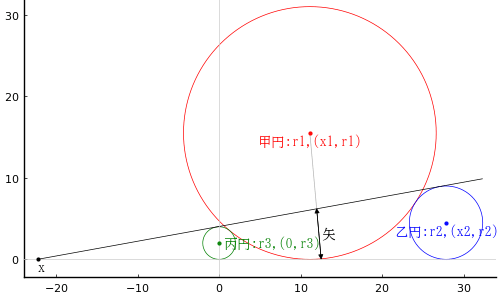
大円の半径と中心座標を r1, (a - r1, r1), (r1, a - r1)
小円の半径と中心座標を r2, (r2, r2)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, r1::positive, r2::positive
eq1 = (a - r1 - r2)^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = (a - r1 - r2)^2 + (r1 - r2)^2 - 2(a - 2r1)^2
res = solve([eq1, eq2], (r1, r2))[1] # 1 of 4
(-(-69*a^3 - 164*a^3*(-3*sqrt(2) - sqrt(3)*sqrt(57 - 40*sqrt(2))/2 + 5)^2 + 8*a^3*(-3*sqrt(2) - sqrt(3)*sqrt(57 - 40*sqrt(2))/2 + 5)^3 + 254*a^3*(-3*sqrt(2) - sqrt(3)*sqrt(57 - 40*sqrt(2))/2 + 5))/(84*a^2), a*(-3*sqrt(2) - sqrt(3)*sqrt(57 - 40*sqrt(2))/2 + 5))
r1 = res[1] |> simplify |> sympy.sqrtdenest |> simplify
r1 |> display
r1 |> println
a*(-4*sqrt(2) - 2*sqrt(6) + 3*sqrt(3) + 6)/2
r2 = res[2] |> simplify |> sympy.sqrtdenest |> simplify
r2 |> display
r2 |> println
a*(-4*sqrt(6) - 6*sqrt(2) + 5*sqrt(3) + 10)/2
3 円の中心間距離がすべて等しくなるのは,大円,小円の半径が,正方形の一辺の長さの (-4*sqrt(2) - 2*sqrt(6) + 3*sqrt(3) + 6)/2 倍と (-4*sqrt(6) - 6*sqrt(2) + 5*sqrt(3) + 10)/2 倍のときである。
正方形の一辺の長さが 1 のとき,大円,小円の半径は 0.3201593438239474,0.18850684623655134 である。
2 円の中心間距離は √2(1 - 2r1) = 0.5086661900605006 である。
(-4*sqrt(2) - 2*sqrt(6) + 3*sqrt(3) + 6)/2 # r1
0.3201593438239474
(-4*sqrt(6) - 6*sqrt(2) + 5*sqrt(3) + 10)/2 # r2
0.18850684623655134
√2(1 - 2*0.3201593438239474) # distance
0.5086661900605006

function draw(a, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2) = (-(-69*a^3 - 164*a^3*(-3*sqrt(2) - sqrt(3)*sqrt(57 - 40*sqrt(2))/2 + 5)^2 + 8*a^3*(-3*sqrt(2) - sqrt(3)*sqrt(57 - 40*sqrt(2))/2 + 5)^3 + 254*a^3*(-3*sqrt(2) - sqrt(3)*sqrt(57 - 40*sqrt(2))/2 + 5))/(84*a^2), a*(-3*sqrt(2) - sqrt(3)*sqrt(57 - 40*sqrt(2))/2 + 5))
r1 = a*(-4√2 - 2√6 + 3√3 + 6)/2
r2 = a*(-4√6 - 6√2 + 5√3 + 10)/2
distance = 2(a - 2r1)^2
@printf("a = %g; r1 = %g; r2 = %g; 中心間距離 = %g\n", a, r1, r2, distance)
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
circle(r1, a - r1, r1)
circle(a - r1, r1, r1)
circle(r2, r2, r2, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r1, a - r1, "大円:r1,(r1,a-r1)", :red, :center, :bottom, delta=delta/2)
point(a - r1, r1, "大円:r1,(a-r1,r1)", :red, :center, delta=-delta/2)
point(r2, r2, "小円:r2,(r2,r2)", :green, :center, delta=-delta/2)
point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
point(0, a, " a", :blue, :left, :bottom, delta=delta/2)
end
end;